INSTRUCTIONS TO THE CANDIDATES
- This paper contains two sections; Section I and Section II.
- Answer all the questions in section I and only five questions from Section II.
- Non programmable silent electronic calculators and KNEC Mathematical tables may be used EXCEPT where stated otherwise.
- Show all the steps in your calculations, giving your answers at each stage.

Questions
SECTION I (50MKS)
- A rally car travelled for 2 hours 40 minutes at an average speed of 120km/h. the car consumes an average of 1 litre of fuel for every 4 kilometers. A litre of fuel costs Ksh.59. Calculate the amount of money spent on fuel. (3mks)
- One interior angle of a polygon is equal to 800 and each of the other interior angles are 128°. Find the number of sides of the polygon. (3mks)
-
- Using a pair of compasses and a ruler only construct a triangle ABC and such that AB = 4cm, BC = 6cm and angle ABC = 135°. (2mks)
- Construct the height of triangle ABC in (a) above taking AB as the base, hence Calculate the area of triangle ABC. (2mks)
- Solve the following inequalities and state the integral values (3mks)
2x – 2 ≤ 3x + 1 < x + 11 - Without using mathematical tables or calculators, evaluate
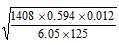 leaving your answer as a simplified fraction (3mks)
leaving your answer as a simplified fraction (3mks) - Two similar solids have surface areas 48cm2 and 108cm2 respectively. Find the volume of the smaller solid if the bigger one has a volume of 162cm3. (3mks)
- A triangle flower garden has an area of 28m2. Two of its edges are 14 metres and 8 metres. Find the angle between the two edges. (3mks)
- A watch which looses a half a minute every hour was set to read the correct time at 0445hr on Monday. Determine in twelve hour system the time the watch will show on Friday at 1845hr the same week. (3mks)
- Simplify the expression: (3mks)
- Use reciprocal and cube root tables to evaluate (3mks)
5 − 3√0.0169
63.34 - A Kenya company received US Dollars M. The money was converted into Kenya Shillings in a bank which buys and sells foreign currencies.
Buying (in Ksh) Selling (in (Ksh)
1 Sterling Pound 125.78 126.64
1 Us Dollar 75.66 75.86- If the company received Ksh.15, 132,000, calculate the amount, M received in US Dollar. (2mks)
- The company exchanged the above Kenya shillings into Sterling pounds to buy a car in Britain. Calculate the cost of the car to the nearest Sterling pound (2mks)
- A trader sold a dress for Ksh 7200 allowing a discount of 10% on the marked price. If the discount had not been allowed the trader would have made a profit of 25% on the sale
of the suit. Calculate the price at which the trader bought the dress. (3mks) - Use logarithms tables to evaluate. (4mks)
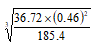
- A certain two-digit number is equivalent to five times the sum of the digits. It is found to be 9 less than the number formed when the digits are interchanged. Find the number. (3mks)
- A man standing 20m away from the foot of a vertical pole observes the top of the pole at an angle of elevation of 300. He begins to walk along a straight line on level ground towards
the pole. Calculate how far he walked before the angle of elevation of the top of the pole becomes 800. (3mks) - Find the acute angle y if sin 4y = cos 2y (2mks)
SECTION II (50MKS)
- Mambo poured spirit into a test tube which has hemispherical bottom of inner radius 1.5cm. He noted that the spirit is 8cm high.
- What is the area of surface in contact with spirit? (4mks)
- Calculate volume of spirit in the test tube. (4mks)
- If Mambo obtained the mass of the spirit as 10g. Calculate the density of the spirit. (2mks)
- The figure below C is a point on AB such that AC: CB=3:1 and D is the mid –point of OA. OC and BD intersect at X.
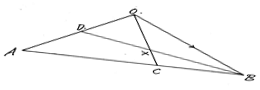
Given that OA = a and OB = b- Write the vectors below in terms of a and b.
- AB (1mk)
- OC (2mks)
- BD (1mk)
- If BX = hBD, express OX in terms of a, b, and h. (1mk)
- If OX = KOC, find h and k. (4mks)
- Hence express OX in terms of a and b only. (1mk)
- Write the vectors below in terms of a and b.
- A straight line L1 has a gradient −½ and passes through point P (−1, 3). Another line L2 passes through the points Q (1,−3) and R (4, 5). Find.
- The equation of L1. (2mks)
- The gradient of L2. (1mk)
- The equation of L2. (2mks)
- The equation of a line passing through a point S (0, 5) and is perpendicular to L2. (3mks)
- The equation of a line through R parallel to L1. (2mks)
- A certain number of people agreed to contribute to buy novels worth sh. 1200. Five of them pulled out and the others agreed to contribute an extra Sh. 10 each. Their contribution brought novels worth sh.200 more than they originally expected.
- If the original number of people was x, write an expression of how much each was to contribute. (1mk)
- Write down two expressions on how much each contributed after the five pulled out and reduced them to a single equation. (2mks)
- Calculate how many people made the contribution (5mks)
- How much did each contribute? (2mks)
-
- In 2001 the total cost of manufacturing an article was Sh.1250 and this was divided between the cost of material, labour and transport in the ratio 8: 14: 3. In 2004 the cost of the material was doubled, labour cost increased by 30% and transport costs increased by 20%.
Calculate the cost of manufacturing the article in 2004. (6mks) - For the same article in (a) above, the cost of manufacturing in 2005 was sh. 1981 as a result of increase in labour costs only. Find the percentage increase in labour cost of 2004. (4mks)
- In 2001 the total cost of manufacturing an article was Sh.1250 and this was divided between the cost of material, labour and transport in the ratio 8: 14: 3. In 2004 the cost of the material was doubled, labour cost increased by 30% and transport costs increased by 20%.
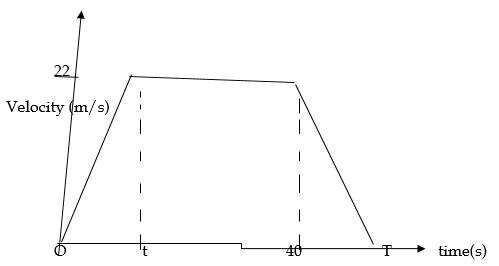
- The figure below shows a velocity – time graph of a car journey.
The car starts from rest and accelerates at 2.75m/s2 for t seconds until its speed is 22m/s. It then travels at this velocity until 40 seconds after starting. Its breaks bring it uniformly to rest. The total journey is 847m long and takes T seconds.
Calculate the- Value of t (3mks)
- Distance travelled during the first t seconds (2mks)
- Value of T (3mks)
- Final deceleration (2mks)
- A triangle with A(−4, 2), B(−6, 6) and C(−6, 2) is enlarged by a scale factor −1 and centre (−2, 6) to produce triangle A¹B¹C¹.
- Draw triangle ABC and A¹B¹C¹.and state its coordinates (4mks)

- Triangle A¹B¹C¹ is then reflected in the line y = x to give triangle A¹¹B¹¹C¹¹.draw A¹¹B¹¹C¹¹.and state its coordinates 3mks
- If triangle A¹¹B¹¹C¹¹ is mapped onto A¹¹¹B¹¹¹C¹¹¹ whose co-ordinates are A¹¹¹(0, −2), B¹¹¹(4, −4) and C¹¹¹(0, −4) by a rotation. Find the centre and angle of rotation. (3mks)
- Draw triangle ABC and A¹B¹C¹.and state its coordinates (4mks)
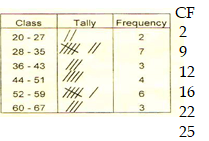
- The following are masses of 25 people taken in a clinic.
20 35 29 45 60
66 56 29 48 37
59 64 24 28 32
35 45 48 52 55
54 55 36 39 35- Using a class width of 8 and starting with the lowest mass of the people. Make a frequency distribution table for the data. (3mks)
- Calculate the median mass of the people. (3mks)
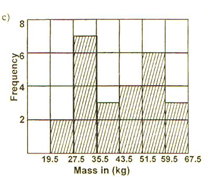
- On the grid provided, draw a histogram to represent the information. (4mks)


Marking Scheme
- 2 + 40/60 = 22/3 hours
22/3 x 120 = 320 km
320/4 = 80 litres
80x59 = 4720 sh. - x + 80 = 180 ⇒ x = 100
180 − 128 = 52
52n + 100 = 360
52n = 260
n = 5
n = 5+1 = 6 -
- h = 4.2 ± 0.1 cm
A = ½ × 4 × 4.2
= 8.4 cm2
- 2x – 2 ≤ 3x+1
–2 – 1 ≤ 3x – 2x
–3 ≤ x
3x + 1 < x + 11
2x < 10
x < 5
–3 ≤ x < 5
Integral values –3, –2, –1, 0, 1, 2, 3, 4 - √1408X594 x 12
605 x 125 x 100
√128 x 54 x 12
5 x 125 x100
√[128 x 9 x 2 x 3 x 3 x 2]
100 x 625
= 72
625 - ASF = 48/108 = 4/9
LSF = √(4/9) = 2/3
VSF= (2/3)3 = 8/27
Vol = 8/27 x 162
=48cm3 - 0.5 x 14 x 8sinθ = 28m2
Sinθ = 0.5
θ = Sin-1(0.5)
Ө = 30º - Tuesday - Thursday = 24x3 = 72hours
Monday = 2400 − 0445 = 19hours 15minutes
Friday = 18hours 45minutes
Total time=72 + 19.25 + 18.75 = 110hours
Time lost = 0.5 x 110 = 55minutes
1845hrs − 55minutes = 1750hours
=5.50pm - N=9t2−25a2=(3t−5a)(3t+5a)
D=6t2+19at+15a2 = 6t2+9at+10at+15a2
=3t(2t+3a)+5a(2t+3a)
=(3t+5a)(2t+3a)
N=(3t−5a)(3t+5a)
D ( 3t+5a)(2t+3a)
=3t−5a
2t+3a 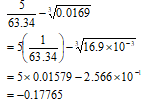
-
- M = 15,132,000
75.66
= 200.000 US Dollars
15,132,000
126.64 - 11944 Sterling pounds
- M = 15,132,000
- Marked Price = 100 x 7200
90
= sh 8000
Selling price = 100 x 8000
125
=sh6400 - Let the no. be xy
10x + y = 5 (x + y) (i)
(10y + x) − (10x + y) = 9 (ii)
−4y + 5x = 0
9y − 9x = 9
−36y + 45x = 0
36y - 36 = 36
9x = 36
x = 4
y = 5
The number is 45 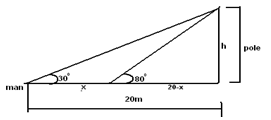
Tan80º = h
20 - x
h = (20 - x) tan80 (i)
Also tan 30 = h
20
h = 20 tan30 (ii)
20tan30 = (20 − x) tan 80
11.547 = 113.425 − 5.6711x
5.671x = 101.878
x = 17.96
≅18m- Sin 4y = Cos 2y
4yº + 2yº= 90º
6yº = 90º
y = 15º -
- Surface area of hemisphere=2πr2
S.A= 2xπ x1.52
= 14.14cm2
Surface area of cylindrical part
= 2πrh
S.A = 2xπ x r x h
22π x 1.5 x 6.5=61.29cm2
T.S.A=14.14+61.29
=75.43cm2 - Volume of hemispherical part=2/3πr3
=2/3 x π x 1.53
=7.071cm3
Volume of cylindrical part=πr2h
=π x 1.52 x 6.5
=45.96cm3
T. volume=7.069+45.96
=53.04cm3 - Density=M/V
=10/53.04
=0.1886 g/cm3
- Surface area of hemisphere=2πr2
-
-
- AB = b - a
- OC = ¼ a + 3/4 b
- BD = ½a - b
- OX=b(1-h)+½ ah
- OX=b(1-h)+½ ah
OX=¼ak + 3/4 bk
½ah =1/4 ak
2 h = k
3/4b k = b (1 − h)
3/4k = 1 − h
3/4(2h) = 1 − h
5/2h = 1 ⇒ h = 2/5
k = 2(2/5) = 4/5
k = 4/5 - 1/5a + 3/5 b
-
-
- y − 3 = ½
x + 1
y - 3 = −½x − ½
y = −½x + 5/2 - g = 5 −−3
4 − 1
= 8/3 - y − 5 = −8/3
x − 4
y - 5 = 8/3 x − 17/3 - y - 5 = −3/8
x
y = −3 x + 5
8 - y − 5 = −½
x − 4
y = −½x + 7
- y − 3 = ½
- 1200
x
1200 + 10 (i)
x
1200+ 200 =1400(ii)
x - 5 x - 5
x2 − 25x − 600 = 0
x2 − 40x − 15x − 600 = 0
x(x − 40) + 15(x − 40) = 0
x = −15 or x = 40
No of people = 40 − 5 = 35
1400 = Sh40
35 - Total ratio = 8+14+3=25
Material = 8/25 x 1250 = 440
Labour = 14/25 x 1250 = 700
Transport = 3/25 x 1250 = 150
2004
Material = 400 x 2 = 800
Labours = 130/100 x 700 = 910
Transport = 120/100 x 150 = 180
Total in 2004 = (1800 + 910 + 180)
= Sh 1890
In 2005 increased to 1981due to labour only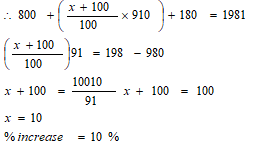
-
- a =v−u/t
2.75 = 22−0/t
t=22/2.75
= 8 sec - Distance = ½ x 8 x 22
= 88m - 847 = ½ ( 40 + t) + 32) x 22
847 = ½ (72 + t) x 22
1694 = (72 + t) 22
1694/22 = 72 + t
77=72+t
T = 5 sec
T = 40 + t = 40+5 = 45 sec. - a =v−u/t = 0−22/5
= −4.4m/s2
- a =v−u/t
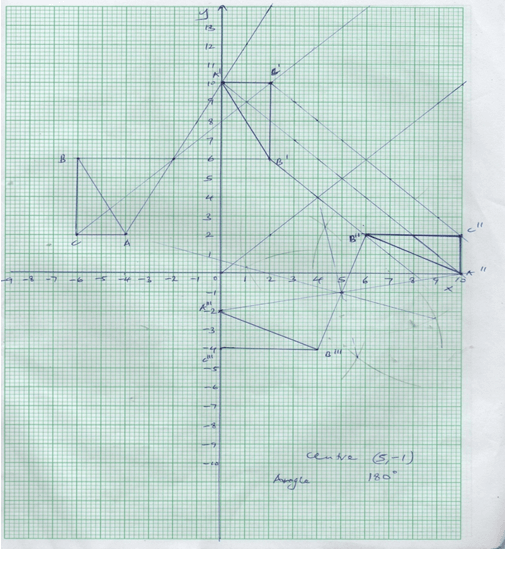
- A’(0,10)
B’(2,6)
C’(2,10) - A”(10,2)
B”(6,2) 3
C”(10,2) - Centre = (5, −1)
Angle = 1800
- A’(0,10)
-
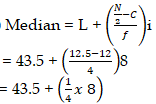
= 43.5 + (1/4 x 8)
= 43.5 + 1
= 44.5-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE 2022 Prediction.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students