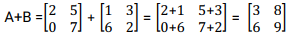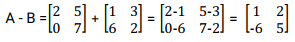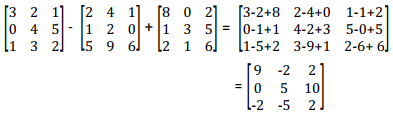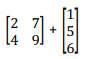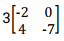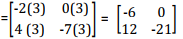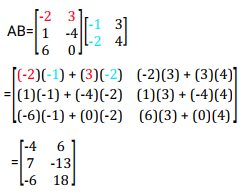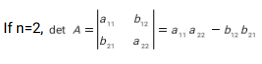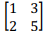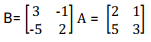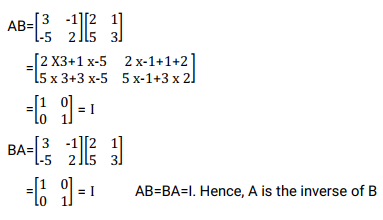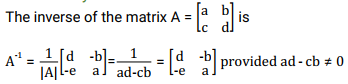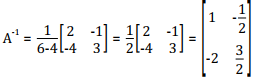- Introduction
- Order of Matrix
- Elements of Matrix
- Addition and Subtraction of Matrices
- Matrix Multiplication
- Identity Matrix
- Determinant Matrix
- Inverse of a Matrix
- Solutions of Simultaneous Linear Equations using Matrix Method
- Past KCSE Questions on the Topic

Introduction
- A matrix is a rectangular arrangement of numbers in rows and columns.
- For instance, matrix A below has two rows and three columns. The dimensions of this matrix are 2 x 3 (read “2 by 3”).
- The numbers in a matrix are its entries. In matrix A, the entry in the second row and third column is 5.
- Some matrices (the plural of matrix) have special names because of their dimensions or entries.

Order of Matrix
- Matrix consist of rows and columns. Rows are the horizontal arrangement while columns are the vertical arrangement.
- Order of matrix is being determined by the number of rows and columns. The order is given by stating the number of rows followed by columns.
Note;
- If the number of rows is m and the number of columns n, the matrix is of order m×n.
E.g. If a matrix has m rows and n columns, it is said to be order m×n.

Elements of Matrix
- The element of a matrix is each number or letter in the matrix. Each element is locating by stating its position in the row and the column.
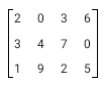
- For example, given the 3 x 4 matrix
- The element 1 is in the third row and first column.
- The element 6 is in the first row and forth column.
Note;
- A matrix in which the number of rows is equal to the number of columns is called a square matrix.
- [ a1, a2 .... an] Is called a row matrix or row vector.
-
-
- [−2 −3 −4] is a row vector of order 1 × 3.
- Two or more matrices re equal if they are of the same order and their corresponding elements are equal.
- Thus, if
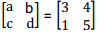 then, a = 3, b = 4 and d = 5.
then, a = 3, b = 4 and d = 5.

Addition and Subtraction of Matrices
- Matrices can be added or subtracted if they are of the same order. The sum of two or more matrices is obtained by adding corresponding elements. Subtraction is also done in the same way.
Example
- A + B
- A – B
Solution
Example
Note;
After arranging the matrices you must use BODMAS
The matrix above cannot be added because they are not of the same order. is of order 2 x 2 while
is of order 3 x1

Matrix Multiplication
To multiply a matrix by a number, you multiply each element in the matrix by the number.
Example
Solution
Example
Solution
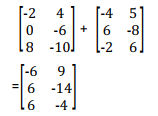
Example
A woman wanted to buy one sack of potatoes, three bunches of bananas and two basket of onion. She went to kikuyu market and found the prices as sh 280 for the sack of potatoes ,sh 50 for a bunch of bananas and sh 100 for a basket of onions. At kondelee market the corresponding prices were sh 300, sh 48 and sh 80.
- Express the woman’s requirements as a row matrix
- Express the prices in each market as a column matrix
- Use the matrices in (a) and (b) to find the total cost in each market
Solution
- Requirements in matrix form is [1 3 2]
-

- Total cost in shillings at Kikuyu Market is

Note;
- The product of two matrices A and B is defined provided the number of columns in A is equal to the number of rows in B.
- If A is an m x n matrix and B is an n x p matrix, then the product AB is an m a p matrix.
A X B = AB
m X n n X p = m X p - Each time a row is multiplied by a column
Example
Solution
Because A is a 3 x 2 matrix and B is a 2 x 2 matrix, the product AB is defined and is a 3 x 2 matrix. To write the elements in the first row and first column of AB, multiply corresponding elements in the first row of A and the first column of B. Then add. Use a similar procedure to write the other entries of the product.


Identity Matrix
- For matrices, the identity matrix or a unit matrix is the matrix that has 1 ’s on the main diagonal and 0’s elsewhere.
- The main diagonal is the one running from top left to bottom right .It is also called leading or principle diagonal. Examples are;

- If A is any n x n matrix and I is the n x n identity matrix, then IA = A and AI = A.

Determinant Matrix
- The determinant of a matrix is the difference of the products of the elements on the diagonals.
Examples
The determinant of A, det A or |A| is defined as follows:
Example
Find the determinant of
Solution
Subtract the product of the diagonals
1 x 5 – 2 x 3 = 5 – 6 = –1
Determinant is –1

Inverse of a Matrix
Two matrices of order n x n are inverse of each other if their product (in both orders) is theidentity matrix of the same order n x n. The inverse of A is written as A-1
Example
Show that
Solution
Note;
To get the inverse matrix
- Find the determinant of the matrix. If it is zero, then there is no inverse
- If it is non zero, then;
- Interchange the elements in the main diagonal
- Reverse the signs of the element in the other diagonals
- Divide the matrix obtained by the determinant of the given matrix
In summary
Example
Find the inverse of
Solution
Check
You can check the inverse by showing that AA-1 = identity matrix

Solutions of Simultaneous Linear Equations Using Matrix Method
Using matrix method solve the following pairs of simultaneous equation
x + 2y = 4
3x - 5y = 1
Solution


Past KCSE Questions on the Topic
- A and B are two matrices. If
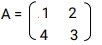 find B given that A2 = A + B
find B given that A2 = A + B - Given that
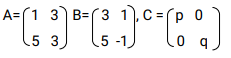 and AB =BC, determine the value of P
and AB =BC, determine the value of P - A matrix A is given by A =
- Determine A2
- If
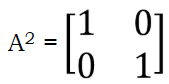 determine the possible pairs of values of x and y
determine the possible pairs of values of x and y
-
- Find the inverse of the matrix
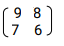
- In a certain week a businessman bought 36 bicycles and 32 radios for total of Kshs 227 280. In the following week, he bought 28 bicycles and 24 radios for a total of Kshs 1 74 960. Using matrix method, find the price of each bicycle and each radio that he bought
- In the third week, the price of each bicycle was reduced by 1 0% while the price of each radio was raised by 1 0%. The businessman bought as many bicycles and as many radios as he had bought in the first two weeks. Find by matrix method, the total cost of the bicycles and radios that the businessman bought in the third week.
- Find the inverse of the matrix
- Determine the inverse T-1 of the matrix
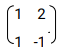 Hence find the coordinates to the point at which the two lines x + 2y=7 and x-y=1
Hence find the coordinates to the point at which the two lines x + 2y=7 and x-y=1 - Given that
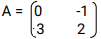 and
and 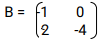 Find the value of x of
Find the value of x of - A – 2x = 2B
- 3x – 2A = 3B
- 2A – 3B = 2x
- A – 2x = 2B
- Find the non- zero value of k for which k
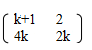 is an inverse.
is an inverse. - A clothes dealer sold 3 shirts and 2 trousers for Kshs. 840 and 4 shirts and 5 trousers for Kshs 1680. Form a matrix equation to represent the above information. Hence find the cost of 1 shirt and the cost of 1 trouser.
Download Matrices - Mathematics Form 3 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students