Introduction
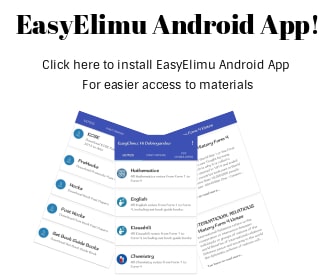
- Consider the right – angled triangle OAB
sinθ = AB
r
AB = rsinθ
OA = rcosθ
Since triangle OAB is right- angled
OA2 + AB2 = OB2(pythagoras theorm)
(rcosθ)2 + (rsinθ)2 = r2
Divide both sides by r2 gives
cos2θ + sin2θ = 1
tanθ = sinθ
cosθ
Example
If tanθ = a show that;
cosθ(sin2θ+cos2θ) = 1
sinθ a
Solution
Factorize the numerator gives and since sin2θ + cos2 θ= 1
But sinθ = tanθ
cosθ
Therefore, = cosθ = 1 = 1
sinθ tanθ a
Example
Show that
(1-cosθ)(1+cosθ) = tan2θ
(1-sinθ)(1+sinθ)
Removing the brackets from the expression gives
1 -cos2θ reason [(A-B)(A+B)=(A2-B2)]
1-sin2θ
Using sin2θ + cos2θ = 1
sin2θ + 1 = cos2θ
Also
1-cos2θ = sin2θ
Therefore
1 -cos2θ =sin2θ = tan2θ
1-sin2θ cos2θ
Example
Given that sinθ = 1/3, find- cos2θ
- tan2θ
- tan2θ + cos2θ
Solution
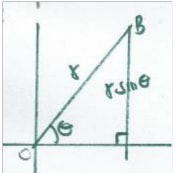
Using the right angle triangle below.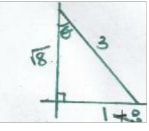
- cosθ = √8
3
therefore cos2θ = (√8/3)2 =8/9 - tan2θ = ( 1/√8)2= 1/8
- tan2θ + cos2θ = 1/8 + 1/9 =1 1/72

Waves
Amplitude
- This is the maximum displacement of the wave above or below the x axis.
Period
- The interval after which the wave repeats itself
Transformations of Waves
- The graphs of y = sin x and y = 3 sin x can be drawn on the same axis.
- The table below gives the corresponding values of sin x and 3sinx for 0o ≤x ≥720o
x2 0 30 60 90 1 20 1 50 180 210 240 270 300 330 360 390 420 450 480 510 540 570 600 630 660 690 720 Sin x 0 0.50 0.87 1 .00 0.87 0.50 0 -0.50 -0.87 -0.50 -0.87 -0.50 0 0.50 0.87 1.00 0.87 0.50 0 -0.50 -0.87 -1.00 -0.87 -0.5 0 3 sinx 0 1 .50 2.61 3.00 2.61 1 .50 0 -1 .50 -2.61 -1 .50 -2.61 -1 .50 0 1.5 2.61 3.00 2.61 1.50 0 -1.50 -2.61 -3.00 -2.61 -2.61 0 - The wave of y = 3 sin x can be obtained directly from the graph of y = sinx by applying a stretch scale factor 3 , x axis invariant .
Note; - The amplitude of y= 3sinx is y =3 which is three times that of y = sin x which is y =1 .
- The period of the both the graphs is the same that is 3600 or 2π
Example
Draw the waves y = cos ½x and y = cos ½x. We obtain y = cos x from the graph y = cos x by applying a stretch of factor 2 with y axis invariant.

Note;
- The amplitude of the two waves are the same.
- The period of y = cos ½x is 4π that is, twice the period of y = cos x

Trigonometric Equations
- In trigonometric equations, there are an infinite number of roots. We therefore specify the range of values for which the roots of a trigonometric equation are required.
Example
Solve the following trigonometric equations:
- Sin 2x = cos x, for 0o ≤ x ≤ 360o
- Tan 3x = 2, for 0o ≤ x ≤ 360o
- 2 sin(x − π/6)
Solution
- Sin 2x = cos x
Sin 2x = sin (90 – x)
Therefore 2 x = 90 – x
X = 30o
For the given range, x =30o and 150o. - Tan 3x = 2
From calculator
3x =63.43o, 243.43o, 423.43o, 603.43o, 783.43oand 321.14o.
In the given range;
x = 21.14o, 81.14o ,141.14o, 201.14o, 261.14o and 321.14o - 2 sin(x − π/6) = − √3
Sin(x − π/6) = √3/2 sin (x − π/6) = − √3/2
x − π/6 = π + π/3, 2π − π/3
x − π/6 = 4/3π , 5/3π
x =3/2πc , 11/6πc

Past KCSE Questions on the Topic
-
- Complete the table for the function y = 2 sin x
x 0o 10o 20o 30o 40o 50o 60o 70o 80o 90o 100o 110o 120o Sin 3x 0 0.5000 -0.8660 y 0 1 .00 -1 .73 -
- Using the values in the completed table, draw the graph of y = 2 sin 3x for 0o ≤ x ≤ 120o on the grid provided
- Hence solve the equation 2 sin 3x = -1.5
- Complete the table for the function y = 2 sin x
- Complete the table below by filling in the blank spaces
Using the scale 1 cm to represent 300 on the horizontal axis and 4 cm to represent 1 unit on the vertical axis draw, on the grid provided, the graphs of y = cosx0 and y = 2 cos ½x0 on the same axis.X0 00 300 600 900 1200 1500 1800 2100 2400 2700 3000 3300 3600 Cos x0 1 .00 0.50 -0.87 -0.87 2 cos ½x0 2.00 1 .93 0.52 -1 .00 -2.00 - Find the period and the amplitude of y = 2 cos ½x0
- Describe the transformation that maps the graph of y = cos x0 on the graph of y = 2 cos ½x0
- Find the period and the amplitude of y = 2 cos ½x0
-
- Complete the table below for the value of y = 2 sin x + cos x.
X 00 300 450 600 900 1200 1350 1500 1800 2250 2700 3150 3600 2 sinx 0 1 .4 1 .7 2 1 .7 1 .4 1 0 -2 -1 .4 0 Cos x 1 0.7 0.5 0 -0.5 -0.7 -0.9 -1 0 0.7 1 Y 1 2.1 2.2 2 1 .2 0.7 0.1 -1 -2 -0.7 1 - Using the grid provided draw the graph of y=2sin x + cos x for 0o ≤ x ≤ 360o. Take 1 cm represent 300 on the x - axis and 2 cm to represent 1 unit on the axis.
- Use the graph to find the range of x that satisfy the inequalities 2 sinxcosx > 0.5
- Complete the table below for the value of y = 2 sin x + cos x.
-
- Complete the table below, giving your values correct to 2 decimal places.
x 0 10 20 30 40 50 60 70 Tan x 0 2x + 300 30 50 70 90 110 130 150 170 Sin(2x+300) 0.50 1 - On the grid provided, draw the graphs of y = tan x and y = sin ( 2x + 300) for 00 ≤ x 700
Take scale:
2 cm for 100 on the x- axis
4 cm for unit on the y- axis
Use your graph to solve the equation tan x − sin ( 2x + 300) = 0.
- Complete the table below, giving your values correct to 2 decimal places.
-
- Complete the table below, giving your values correct to 2 decimal places
X0 0 30 60 90 120 150 180 2sinx0 0 1 2 1 1–cosx0 0.5 1 - On the grid provided, using the same scale and axes, draw the graphs of y = sin x0 and y = 1 – cos x0 00 ≤ x ≤ 1800
Take the scale:
2 cm for 300 on the x- axis
2 cm for 1 unit on the y- axis - Use the graph in (b) above to
- Solve equation
2 sin xo + cos x0 = 1 - Determine the range of values x for which 2sinxo > 1 – cosxo
- Solve equation
- Complete the table below, giving your values correct to 2 decimal places
-
- Given that y = 8 sin 2x – 6 cos x, complete the table below for the missing values of y, correct to 1 decimal place.
X 00 150 300 450 600 750 900 1050 1200 Y = 8sin2x – 6cosx -6 -1 .8 3.8 3.9 2.4 0 -3.9 - On the grid provided, below, draw the graph of y = 8 sin 2x – 6 cos for 00 ≤ x ≤ 1200
Take the scale
2 cm for 150 on the x- axis
2 cm for 2 units on the y – axis - Use the graph to estimate
- The maximum value of y
- The value of x for which 4 sin 2x – 3 cos x =1
- The maximum value of y
- Given that y = 8 sin 2x – 6 cos x, complete the table below for the missing values of y, correct to 1 decimal place.
- Solve the equation 4 sin (x + 300) = 2 for 00 ≤ x ≤ 3600
- Find all the positive angles not greater than 1800 which satisfy the equation
Sin2x – 2 tan x = 0
Cos x - Solve for values of x in the range 00 ≤ x ≤ 3600 if 3 cos2x – 7 cos x = 6
- Simplify 9 – y2 where y = 3 cos θ
y - Find all the values of θ between 00 and 3600 satisfying the equation 5 sin θ = −4
- Given that sin (90 – x) = 0.8. Where x is an acute angle, find without using mathematical tables the value of tan x0
- Complete the table given below for the functions
y= −3 cos 2x0 and y = 2 sin (3x/20 + 300) for 00 ≤ x ≤ 1800
Using the graph paper draw the graphs of y = -3 cos 2x0 and y = 2 sin (3x/20 + 300)X0 00 200 400 600 800 1000 1200 1400 1600 1800 -3cos 2x0 -3.00 -2.30 -0.52 1 .50 2.82 2.82 1 .50 -0.52 -2.30 -3.00 2sin(3x0 +300) 1 .00 1 .73 2.00 1 .73 1 .00 0.00 -1 .00 -1 .73 -2.00 -1 .73 - On the same axis. Take 2 cm to represent 200 on the x- axis and 2 cm to represent one unit on the y – axis
- From your graphs. Find the roots of 3 cos 2 x0 + 2 sin (3x/20 + 300) = 0
- On the same axis. Take 2 cm to represent 200 on the x- axis and 2 cm to represent one unit on the y – axis
- Solve the values of x in the range 00 ≤ x ≤ 3600 if 3 cos2x – 7cos x = 6
- Complete the table below by filling in the blank spaces
Using the scale 1 cm to represent 300 on the horizontal axis and 4 cm to represent 1 unit on the vertical axis draw on the grid provided, the graphs of y – cos x0 and y = 2 cos ½ x0 on the same axisx0 0 30 60 90 120 150 180 210 240 270 300 330 360 Cosx0 1.00 0.50 -0.87 -0.87 2cos½x0 2.00 1 .93 0.5 - Find the period and the amplitude of y =2 cos ½ x0
Ans. Period = 7200. Amplitude = 2 - Describe the transformation that maps the graph of y = cos x0 on the graph of y = 2 cos½ x0
- Find the period and the amplitude of y =2 cos ½ x0
Download Trigonometry III - Mathematics Form 4 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

