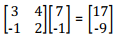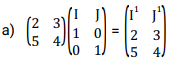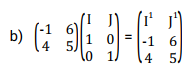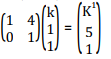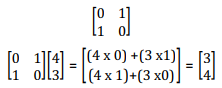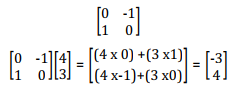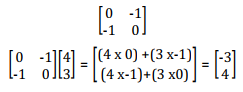- Introduction
- Finding the Matrix of Transformation
- The Unit Square
- Successive Transformations
- Inverse Matrix Transformation
- Area Scale Factor and Determinant of Matrix
- Shear and Stretch
- Isometric and Non-isometric Transformation
- Past KCSE Questions on the Topic

Introduction
- A transformation change the shape, position or size of an object as discussed in book two.
- Pre – multiplication of any 2 x 1 column vector by a 2 x 2 matrix results in a 2 x 1 column vector
Example 1
If the vectoris thought of as a position vector that is to mean that it is representing the points with coordinates (7, -1 ) to the point (17, -9).
Note; - The transformation matrix has an effect on each point of the plan. Let’s make T a transformation matrix
Then T maps points (x, y) onto image points x1 ,y
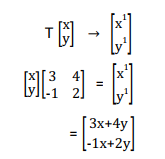

Finding the Matrix of Transformation
- The objective is to find the matrix of given transformation.
Example 2
Find the matrix of transformation of triangle PQR with vertices P (1, 3) Q (3, 3) and R (2, 5).The vertices of the image of the triangles is P1(1,-3) ,Q1(3,-3) and R1(2,-5).
Solution
Let the matrix of the transformation be
Equating the corresponding elements and solving simultaneously
a + 3b = 1
3a + 3b = 3
2a= 2
a = 1 and b = 0
c + 3d = -3
3c + 3d = -3
2c= 0
c = 0 and d = -1
Therefore the transformation matrix is
Example 3
A trapezium with vertices A (1 ,4) B(3,1 ) C (5,1 ) and D(7,4) is mapped onto a trapezium whose vertices are A1(-4,1) ,B1(-1 ,3) ,C1(-1,5) ,D1(-4 ,7).Describe the transformation and find its matrix
Solution
Let the matrix of the transformation be
Equating the corresponding elements we get;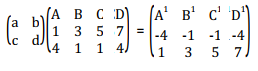
a + 4b = - 4 c + 4d = 1
3a + b = -1 3c + d = 3
Solve the equations simulteneously
3a + 12b = - 12
3a + b = - 1
11b = -11
hence b =-1 or a = 0
3c + 12d = 3
3c + d =3
11d = 0
d = 0 c = 1
The matrix of the transformation is therefore
The transformation is positive quarter turn about the origin
Note; - Under any transformation represented by a 2 x 2 matrix, the origin is invariant, meaning it does not change its position.Therefore if the transformtion is a rotation it must be about the origin or if the transformation is reflection it must be on a mirror line which passses through the origin.

The Unit Square
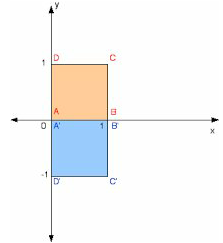
- The unit square ABCD with vertices A (0,0) ,B(1,0) ,C(1,1) and D(0,1) helps us to get the transformation of a given matrix and also to identify what trasformation a given matrix represent.
Example 4
Find the images of I and J under the trasformation whose matrix is;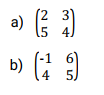
Solution
NOTE; - The images of I and J under transformation represented by any 2 x 2 matrix i.e.,
are I1(a ,c) and J1(b ,d)
Example 5
Find the matrix of reflection in the line y = 0 or x axis.
Solution
Using a unit square the image of B is (1 , 0) and D is (0 , -1 ) .Therefore , the matrix of the transformation is

Example 6
Show on a diagram the unit square and it image under the transformation represented by the matrix
Solution
Using a unit square, the image of I is ( 1 ,0 ), the image of J is ( 4 , 1 ),the image of O is ( 0,0) and that of K is
Therefore ,K1,the image of K is ( 5 ,1)

Successive Transformations
- The process of performing two or more transformations in order is called successive transformation e.g. performing transformation H followed by transformation Y is written as follows YH or if A, B and C are transformations; then ABC means perform C first,then B and finally A , in that order.
- The matrices listed below all perform different rotations/reflections:
- This transformation matrix is the identity matrix. When multiplying by this matrix, the point matrix is unaffected and the new matrix is exactly the same as the point matrix
- This transformation matrix creates a reflection in the x-axis. When multiplying by this matrix, the x coordinate remains unchanged, but the y co-ordinate changes sign.
- This transformation matrix creates a reflection in the y-axis. When multiplying by this matrix, the y coordinate remains unchanged, but the x co-ordinate changes sign.
- This transformation matrix creates a rotation of 1 80 degrees. When multiplying by this matrix, the point matrix is rotated 1 80 degrees around (0, 0). This changes the sign of both the x and y co-ordinates.
- This transformation matrix creates a reflection in the line y=x. When multiplying by this matrix, the x coordinate becomes the y co-ordinate and the y-ordinate becomes the x co-ordinate
- This transformation matrix rotates the point matrix 90 degrees clockwise. When multiplying by this matrix, the point matrix is rotated 90 degrees clockwise around (0, 0).
- This transformation matrix rotates the point matrix 90 degrees anti-clockwise. When multiplying by this matrix, the point matrix is rotated 90 degrees anti-clockwise around (0, 0).
- This transformation matrix creates a reflection in the line y=-x. When multiplying by this matrix, the point matrix is reflected in the line y=-x changing the signs of both co-ordinates and swapping their values.

Inverse Matrix Transformation
- A transformation matrix that maps an image back to the object is called an inverse of matrix.
Note; - If A is a transformation which maps an object T onto an image T1,then a transformation that can map T1 back to T is called the inverse of the transformation A , written as image A-1.
- If R is a positive quarter turn about the origin the matrix for R is
and the matrix for R-1 is
hence R-1R = RR-1 = 1
Example 7
T is a triangle with vertices A (2, 4), B (1 , 2) and C (4, 2).S is a transformation represented by the matrix- Draw T and its image T1 under the transformation S
- Find the matrix of the inverse of the transformation S
Solution- Using transformation matrix S =
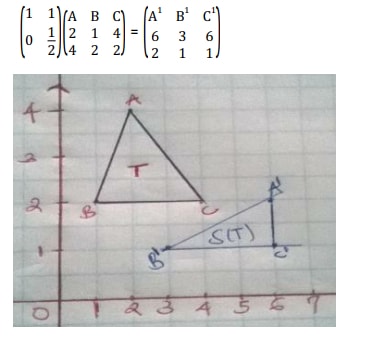
- Let the inverse of the transformation matrix be(ac db). This can be done in the following ways
- S-1S = 1
Therefore
Equating corresponding elements and solving simultaneously;
a = 1 ,b = -2 , c = 0 and d = 2
Therefore
-

- S-1S = 1

Area Scale Factor and Determinant of Matrix
- The ratio of area of image to area object is the area scale factor (A.S.F)
Area scale factor = area of image
area of object - Area scale factor is numerically equal to the determinant. If the determinant is negative you simply ignore the negative sign.
Example 8
Area of the object is 4 cm and that of image is 36 cm find the area scale factor.
Solution
36 = 9
4
If it has a matrix ofthe determinant is 9 - 0 = 9 hence equal to A.S.F

Shear and Stretch
Shear
- The transformation that maps an object (in orange) to its image (in blue) is called a shear
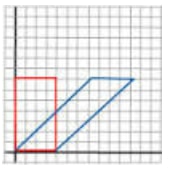
- The object has same base and equal heights. Therefore, their areas are equal. Under any shear, area is always invariant (fixed)
- A shear is fully described by giving;
- The invariant line
- A point not on the invariant line, and its image.
Example 9
A shear X axis invariant
Example 10
A shear Y axis invariant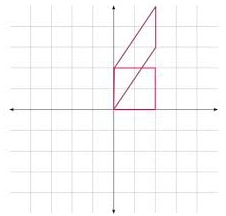
Note; - Shear with x axis invariant is represented by a matrix of the form
under this trasnsformation, J (0, 1 ) is mapped onto J1(k,1).
- Likewise a shear with y – axis invariant is represented by a matrix of the form
. Under this transformation, I (0,1 ) is mapped onto I1(1,k).
Stretch
- A stretch is a transformation which enlarges all distance in a particular direction by a constant factor. A stretch is described fully by giving;
- The scale factor
- The invariant line
- Note;
- If K is greater than 1 , then this really is a stretch.
- If k is less than one 1 , it is a squish but we still call it a stretch
- If k = 1 , then this transformation is really the identity i.e. it has no effect.
Example 11
Using a unit square, find the matrix of the stretch with y axis invariant ad scale factor 3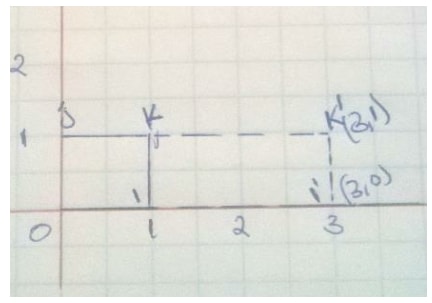
Solution
The image of I is I1(1, 0) and the image of J is (0,1) therefore the matrix of the stretch is - Note;
The matrix of the stretch with the y-axis invariant and scale factor k isand the matrix of a stretch with x – axis invariant and scale factor k is

Isometric and Non-isometric Transformation
- Isometric transformations are those in which the object and the image have the same shape and size (congruent) e.g. rotation, reflection and translation
- Non- isometric transformations are those in which the object and the image are not congruent e.g., shear stretch and enlargement

Past KCSE Questions on the Topic
- Matrix p is given by
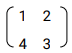 . Find P-1
. Find P-1 - A triangle is formed by the coordinates A (2, 1 ) B (4, 1 ) and C (1 , 6). It is rotated clockwise through 90o about the origin. Find the coordinates of this image.
- On the grid provided, A (1 , 2) B (7, 2) C (4, 4) D (3, 4) is a trapezium
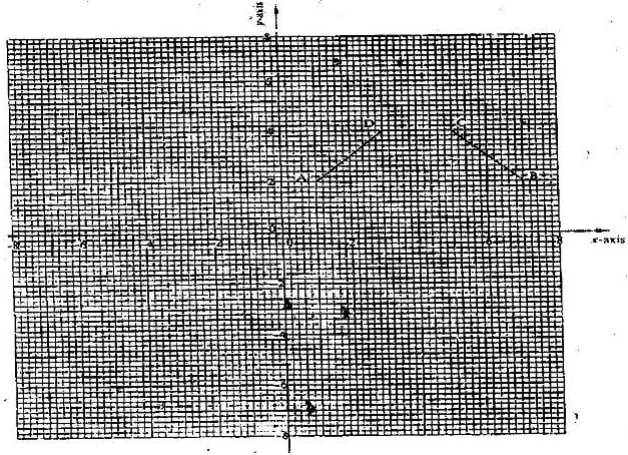
- ABCD is mapped onto A’B’C’D’ by a positive quarter turn. Draw the image A’B’C’D on the grid
- A transformation matrix
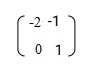 maps A’B’C’D onto A”B” C”D” Find the coordinates of A”B”C”D”
maps A’B’C’D onto A”B” C”D” Find the coordinates of A”B”C”D”
- A triangle T whose vertices are A (2, 3) B (5, 3) and C (4, 1 ) is mapped onto triangle T1 whose vertices are A1 (-4, 3) B1 (-1 , 3) and C1 (x, y) by a Transformation M =
- Find the:
- Matrix M of the transformation
- Coordinates of C1
- Triangle T2 is the image of triangle T1 under a reflection in the line y = x. Find a single matrix that maps T and T2
- Find the:
- Triangles ABC is such that A is (2, 0), B (2, 4), C (4, 4) and A”B”C” is such that A” is (0, 2), B” (-4 ,–10) and C “is (-4, -12) are drawn on the Cartesian plane.
Triangle ABC is mapped onto A”B”C” by two successive transformations
R=Followed by
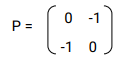
- Find R
- Using the same scale and axes, draw triangles A’B’C’, the image of triangle ABC under transformation R. Describe fully, the transformation represented by matrix R
- Triangle ABC is shown on the coordinate’s plane below
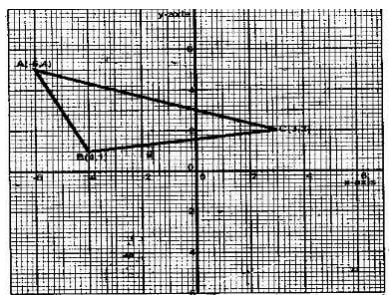
- Given that A (-6, 5) is mapped onto A (6,-4) by a shear with y- axis invariant
- Draw triangle A’B’C’, the image of triangle ABC under the shear
- Determine the matrix representing this shear
- Draw triangle A’B’C’, the image of triangle ABC under the shear
- Triangle A B C is mapped on to A” B” C” by a transformation defined by the matrix
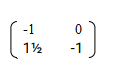
- Draw triangle A” B” C”
- Describe fully a single transformation that maps ABC onto A”B” C”
- Given that A (-6, 5) is mapped onto A (6,-4) by a shear with y- axis invariant
- Determine the inverse T-1of the matrix T =
Hence find the coordinates to the point at which the two lines x + 2y = 7 and x - y =1 - Given that A =
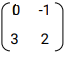 B =
B =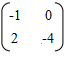
Find the value of x if- A- 2x = 2B
- 3x – 2A = 3B
- 2A - 3B = 2x
- A- 2x = 2B
- The transformation R given by the matrix
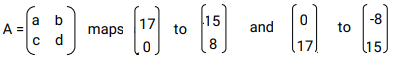
- Determine the matrix A giving a, b, c and d as fractions
- Given that A represents a rotation through the origin, determine the angle of rotation.
- S is a rotation through 180 about the point (2, 3). Determine the image of (1 , 0) under S followed by R
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Matrices and Transformation - Mathematics Form 4 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students