- Introduction
- Delta Notation
- Derivative of a Polynomial.
- Equations of Tangents and Normal to a Curve.
- Stationary Points
- Turning Points
- Applications of Differentiation

Introduction
- Differentiation is generally about rate of change
Example
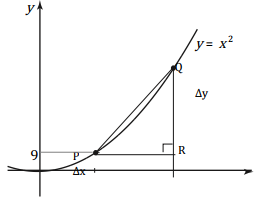
- If we want to get the gradient of the curve y = x2 at a general point (x ,y ).We note that a general point on the curve y = x2 will have coordinates of the form ( x ,x2 ).
- The gradient of the curve y= x2 at a general point ( x, y ) can be established as below.
- If we take a small change in x , say h. This gives us a new point on the curve with co-ordinates [(x +h), (x + h)2]. So point Q is [(x +h), (x + h)2] while point P is ( x,x2).
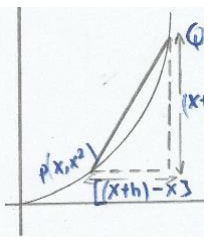
- To find the gradient of PQ = change in Y
change in X
Change in y = (x + h)2 - x2
Change in x = (x + h) - x
Gradient = (x + h)2- x2
(x + h ) - x
= x2+2xh+ h2-x2
x +h-x
=2xh + h2
h
= 2x + h
- By moving Q as close to p as possible, h becomes sufficiently small to be ignored. Thus, 2x +h becomes 2x. Therefore, at general point (x,y)on the curve y = x2,the gradient is 2x.
- 2x is called the gradient function of the curve y = x2.We can use the gradient function to determine the gradient of the curve at any point on the curve.
- In general, the gradient function of y = xn is given by nxn-1,where n is a positive integer. The gradient function is called the derivative or derived function and the process of obtaining it is called differentiation.
- The function y=x5 becomes 5x5-1 = 5x4 when we differentiate it

Delta Notation
- A small increase in x is usually denoted by ∆x similarly a small increase in y is denoted by ∆y. Let us consider the points P (x ,y) and Q [(x + ∆x),(y + ∆y) on the curve y = x2
- Note;
X is a single quantity and not a product of ∆ and x .similarly ∆y is a single quantity.
The gradient of PQ, ∆y = (x+ ∆x)2 - x2
∆x (x+ ∆x) - x
= x2+2x∆x+(∆x)2 - x2
x+∆x-x
= 2x +∆x - As ∆x tends to zero;
- ∆x can be ignored
- ∆y/∆x gives the derivative which is denoted by dy/dx
- thus dy/dx = 2x
- When we find dy/dx, we say we are differentiating with respect to x, For example given y = x4; then = 4x3
- In general the derivatives of y =axn is naxn-1 e.g. y = 5x2 = 10x , y = 6x3 = (6 x 3)x3-1 = 18x2

Derivative of a Polynomial.
- A polynomial in x is an expression of the form a0xn +a1xn-1 +……………an; where a0,a1………. an are constants
- To differentiate a polynomial function, all you have to do is multiply the coefficients of each variable by their corresponding exponents/powers, subtract each exponent/powers by one , and remove any constants.
Steps Involved in Solving Polynomial
Identify the variable terms and constant terms in the equation.
- A variable term is any term that includes a variable and a constant term is any term that has only a number without a variable.
- Find the variable and constant terms in this polynomial function: y = 5x3 + 9x2 + 7x + 3
- The variable terms are 5x3, 9x2, and 7x
- The constant term is 3
Multiply the coefficients of each variable term by their respective powers.
- Their products will form the new coefficients of the differentiated equation. Once you find their products, place the results in front of their respective variables. For example:
- 5x3 = 5x3 = 1 5
- 9x2 = 9x2 = 1 8
- 7x = 7x1 = 7
Lower each exponent by one.
- To do this, simply subtract 1 from each exponent in each variable term. Here's how you do it:
- 5x3 = 15x2
- 9x2 = 18x
- 7x1-1 = 7
Replace the old coefficients and old exponents/powers with their new counterparts.
- To finish differentiating the polynomial equation, simply replace the old coefficients with their new coefficients and replace the old powers with their values lowered by one.
- The derivative of constants is zero so you can omit 3, the constant term, from the final result.
- The derivative of the polynomial y = 15x2 + 18x + 7
- In general, the derivative of the sum of a number of terms is obtained by differentiating each term in turn.
Examples
Find the derived function of each of the following
- S=2t3 - 3t2 + 4t
- A = V2 - 2V + 10
Solution
- dS = 6t2 - 6t + 4
dt - dA = 2v - 2
dv

Equations of Tangents and Normal to a Curve.
- The gradient of a curve is the same as the gradient of the tangent to the curve at that point. We use this principle to find the equation of the tangent to a curve at a given point.
Example
Find the equation of the tangent to the curve;
y = x3 + 2x + 1 at (1,4)
Solution
dy = 3x2+ 2
dx
At the point (1,4), the gradient is 3 x 1 2+ 2 = 5(we have substituted the value of x with 1)
We want the equation of straight line through (1 , 4) whose gradient is 5.
Thus y-4 = 5
x-1
y - 4 = 5x - 5
y = 5x - 1 (this is the equation of the tangent)
- A normal to a curve at appoint is the line perpendicular to the tangent to the curve at the given point.
- In the example above the gradient of the tangent of the tangent to the curve at (1 , 4) is 5. Thus the gradient of the normal to the curve at this point is - 1/5 .
- Therefore, equation of the normal is:
y-4= -1/5
x-1
5(y – 4) = - 1(x – 1)
y =-x+21
5
Example
Find the equation of the normal to the curve y =x3 - 2x - 1 at (1, - 2)
Solution
y = x3 - 2x - 1
dy = 3x2 - 2
dx
At the point ( 1 ,-2) gradient of the tangent line is 1 .Therefore the gradient of the normal is -1 .the required equation is
y-(-2) = - 1
x-1
y+2 = -1
x-1
y + 2 = - x + 1
The equation of the normal is y = -x -1

Stationary Points
Note;
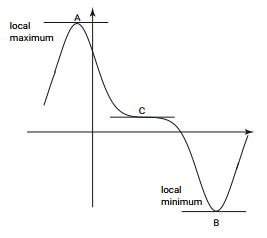
- In each of the points A ,B and C the tangent is horizontal meaning at these points the gradient is zero. So dy/dx = 0 at points A,B, C.
- Any point at which the tangent to the graph is horizontal is called a stationary point. We can locate stationary points by looking for points at which dy/dx= 0.

Turning Points
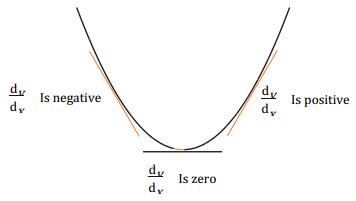
- The point at which the gradient changes from negative through zero to positive is called minimum point while the point which the gradient changes from positive through zero to negative is called maximum point
- In the figure above A is the maximum while B is the minimum.
Minimum point
- Gradient moves from negative through zero to positive.
Maximum point
- Gradient moves from positive through zero to negative.
The maximum and minimum points are called turning points.
A point at which the gradient changes from positive through zero to positive or from negative zero to negative is called point of inflection.
Example
Identify the stationary points on the curve y =x2 - 3x + 2.for each point, determine whether it is a maximum, minimum or a point of inflection.
Solution
y = x3 - 3x + 2
dy =3x2 - 3
dx
At stationary point,dy/dx = 0
Thus 3x2 - 3 = 0
3(x2-1) = 0
3(x+1)(x-1) = 0
x = - 1 or x = 1
when = -1 ,y = 4
when x = 1 , y = 0
Therefore, stationary points are (-1, 4) and (1 ,0).
Consider the sign of the gradient to the left and right of x = 1
| x | 0 | 1 | 2 |
| dy dx |
-3 | 0 | 9 |
| Diagrammaticrepresentation | \ | ___ | / |
Therefore (1, 0) is a minimum point.
Similarly, sign of gradient to the left and right of x = -1 gives
| x | -2 | -1 | 0 |
| dy dx |
9 | 0 | -3 |
| Diagrammatic representation | / | ___ | \ |
Therefore (-1 , 4) is a maximum point.
Example
Identify the stationary points on the curve y =1 + 4x3 - x4.Determine the nature of each stationary point.
Solution
y =1 + 4x3 − x4
dy= 12x2 −4x3
dx
At stationary points,dy/dx = 0
12x2 - 4x3 = 0
4x2(3−x) = 0
x = 0 or x = 3
Stationary points are (0, 1) and (3, 28)
Therefore (0, 1 ) is a point of inflection while (3, 28) is a maximum point.

Applications of Differentiation
Calculation of Velocity
If the displacement, S is expressed in terms of time t, then the velocity is v =dS/dt
Example
The displacement, S metres, covered by a moving particle after time, t seconds, is given by S =2t3 + 4t2 - 8t + 3.Find
- Velocity at :
- t = 2
- t= 3
- Instant at which the particle is at rest.
Solution
S =2t3 + 4t2 - 8t + 3
The gradient function is given by;
V =dS
dt
= 6t2 + 8t - 8
- velocity
- at t = 2 is ;
v = 6 x 22 + 8 x 2 - 8
= 24 + 16 – 8
=32m/s - at t = 3 is ;
v = 6 x 3 2 + 8 x 3 - 8
= 54 + 24 – 8
=70m/s
- at t = 2 is ;
- the particle is at rest when v is zero
6t2 + 8t - 8 = 0
2(3t2+4t-4) = 0
2(3t-2)(t+2) = 0
t = 2/3 or t = - 2
It is not possible to have t = -2
The particle is therefore at rest at t = 2/3 seconds
Calculation of Acceleration
Acceleration is found by differentiating an equation related to velocity. If velocity v , is expressed in terms of time, t , then the acceleration, a, is given by a = dv/d
Example
A particle moves in a straight line such that is its velocity v ms-1 after t seconds is given by v = 3 + 10t − t2.
Find
- the acceleration at :
- t =1 sec
- t =3 sec
- t =1 sec
- the instant at which acceleration is zero
Solution
- v = 3 + 10t + t2
a = dv = 10 - 2t
dt- At t = 1 sec a = 10 – 2 x 1
= 8 ms-2 - At t = 3 sec a = 10 – 2 x 3
= 4 ms-2
- At t = 1 sec a = 10 – 2 x 1
- Acceleration is zero when dy/dt = 0
Therefore, 10 – 2t = 0 hence t = 5 seconds
Example
A closed cylindrical tin is to have a capacity of 250π ml. if the area of the metal used is to be minimum, what should the radius of the tin be?
Solution
Let the total surface area of the cylinder be A cm2,radius r cm and height h cm.
Then, A = 2πr2 + 2 πrh
Volume = 2πr2h = 250πcm2
πr2h = 250π
Making h the subject,
h = 250π
πr2
= 250
r2
Put h =250/r2 in the expression for surface area to get;
A = 2 πr2 + 2 πr×250r2
=2πr2 + 500πr−1
dA = 4πr - 500πr−2
dr
For minimum surface area,dA/dr = 0
4πr - 500π/r2 = 0
4πr3 - 500π = 0
4r3 = 500
r3 = 500/4 = 125
r = 3√125
= 5
Therefore the minimum area when r = 5 cm
Example
A farmer has 100 metres of wire mesh to fence a rectangular enclosure. What is the greatest area he can enclose with the wire mesh?
Solution
Let the length of the enclosure be x m. Then the width is 100-2x m = (50-x)m
2
Then the area A of the rectangle is given by;
A = x(50 –x)m2
= 50x – x2 m2
For maximum or minimum area,
dA = 0
dx
Thus, 50 – 2x = 0
x = 25
The area is maximum when x = 25 m
That is A = 50 X 25 – (25)2
= 625 m2.
Download Differentiation - Mathematics Form 4 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students