Introduction
- When heat is transferred from one body to another, the body which loses heat has its temperature lowered while that which gains heat has its temperature raised.

Terms Used
-
Heat Capacity, C.
This is the quantity of heat energy required to raise the temperature of a given mass of substance by one Kelvin.
i.e. heat capacity, C = Q(J)/Δθ(K)
Hence the SI Unit of heat capacity is joule per Kelvin (JK-1). -
Specific Heat Capacity, c
This is the quantity of heat energy required to raise the temperature of a unit mass of a substance by one Kelvin.
i.e . c = Q(J)/mΔθ(KgK)
Q = mcΔθ
The SI Unit of specific heat capacity is joules per kilogram per Kelvin (JKg-1K-1 ).
Note that c = C/m
Therefore heat capacity, C = mass, m × specific heat capacity, c.
The table below shows some substances with their specific heat capacities:
Material s.h.c ( JKg-1K-1) Water 4200 Alcohol 2300 Kerosene 2200 Ice 220 Aluminium 900 Glass 830 Iron 460 Copper 390 Mercury 140 Lead 130
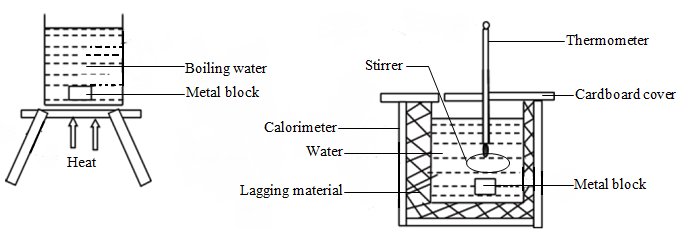
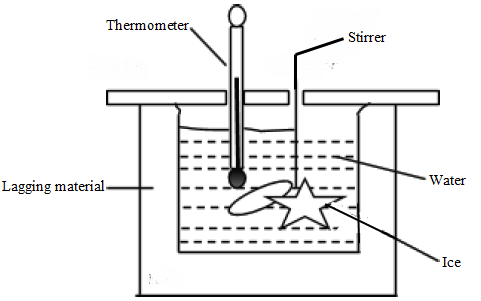
Determination of the specific heat capacity
By the method of mixtures
- Specific heat capacity of solids
In this method, a known mass of a solid, e.g. a metal block is heated by dipping it in a bath of hot water.
After some time, the solid is very fast transferred into cold water in a calorimeter and whose mass is known.
The calorimeter is then covered using a piece of cardboard and stirred continuously.
The following measurements are then recorded:
- Mass of the solid metal block, ms
- Mass of copper calorimeter with the stirrer, mc
- Mass of the calorimeter and stirrer + water, m1
- Temperature of the boiling water (initial temperature of the metal block), θs
- Temperature of cold water in the calorimeter (initial temperature of calorimeter), θw
- Final steady temperature of the mixture, θ
Calculation
Mass of the water in the calorimeter = m1 – mc = mw
Temperature change of the hot metal block = θs – θ
Temperature change of the water in the calorimeter and the calorimeter = θ − θw
Assuming there is no heat loss to the surrounding when the metal block is being transferred into the cold water and thereafter;
Amount of heat lost by the metal block = amount of heat gained by calorimeter with stirrer + amount of heat gained by water in the calorimeter.
i.e. m s c s (θs − θ) = mccc (θ − θw) + mwcw(θ − θw)
where:
cs – s.h.c. of the metal block
cc – s.h.c. of the copper calorimeter
cw – s.h.c. of water.
Hence s.h.c. of the metal block, cs =[mc cc(θ − θw) + mwcw (θ − θw)]/ms(θs − θ) - Specific heat capacity of a liquid
In this case, a solid of known s.h.c. is used and the water in the calorimeter is replaced with the liquid whose s.h.c. is to be determined.
The solid metallic block is first heated in a bath of boiling water and then transferred into the calorimeter containing the liquid.
The following measurements are then collected:
- Mass of the metal block, ms
- Mass of the calorimeter with stirrer, mc
- Mass of the calorimeter, stirrer and the liquid, m1
- Initial temperature of the metal block, θs
- Initial temperature of the liquid, θl
- Final steady temperature of the mixture, θ
If the there is no heat loss to the surrounding, then the quantity of heat lost by the metal block equals the quantity of heat gained by the calorimeter with stirrer and the liquid.
i.e. mscs (θs – θ) = [mccc (θ-θl ) + mlcl(θ − θl)]
Hence cl = [mccs(θs – θ) − mccc (θ − θl)]/ml(θ − θl)
Alternatively the s.h.c. of a liquid can be obtained by mixing it with another liquid whose specific heat capacity is known and their common temperature determined.
The following precautions must be taken to minimize heat losses to the surroundings:
- Using a highly polished calorimeter
- Heavily lag the calorimeter
- Using a lid of poor thermal conductivity
Example 7.1
- 70g of a solid initially at 25oC was carefully dropped into water in a calorimeter at 60oC. If the final constant temperature of the water and the solid was 54oC and the mass of water is 500g, determine the specific heat capacity of the solid. Assume the heat absorbed by the calorimeter to be negligible. Take the s.h.c. of water = 4200JKg-1K-1.
{ans. 10, 767.23JKg-1K-1}
Solution
Heat lost = heat gained
mwcwΔθw = mscsΔθs
0.5Kg × 4200JKg-1K-1 × (60-54)K = 0.07kg × cs × (54 − 25)K
Cs = 29400J/5.73KgK ×= 10,767.23 JKg-1K-1 - A student heated 20Kg of water to a temperature of 80oC. He then added x Kg of water at 15o C and the final steady temperature of the mixture is 40 0 C. Given that the s.h.c. of water is 1.2Jg-1K-1, determine the value of x. {ans. 32kg}
Solution
Heat lost = heat gained
20kg × 4200Kg-1K-1 × (80 − 40) K = x × 4200JKg-1K-1 × (40 − 15)K
X = 3,360,000/25, 000 = 32kg. - 0.2kg of iron at 20 0 C is dropped into 0.09kg of water at 26 0 C inside a calorimeter of mass 0.15kg and s.h.c. 800JKg-1K-1. Find the final temperature of the water. Take the s.h.c. of iron = 460JKg-1 K-1 and that of water = 4200JKg-1K-1. {ans. 33.2oC}
Solution
Heat lost by iron = heat gained by calorimeter + heat gained by water.
0.2kg × 460JKg-1K-1×(20-θc )K = 0.15kg×800JKg-1K-1×(θc -26) + 0.09Kg×4200JKg-1K-1×(θc − 26)
9200-92θc = 126θc − 3120 + 378θc − 9828
596θc = 22148
θc = 22148/596 = 33.2oC - A certain block is heated such that its temperature is raised from 15 0 C to 45 0 C. calculate the amount of heat absorbed by the metal if its heat capacity is 460JK-1
{13, 800J}
Solution
Q = C × Δθ = 460JK-1 × (45 − 15)K = 13,800J. - In an experiment to determine the specific heat capacity of a metal, a 20g of the metal was transferred from boiling water to a lagged copper calorimeter containing cold water. The water was stirred and a final steady temperature was realized. The following data was recorded:
-initial temperature of cold water and calorimeter =20oC
-temperature of boiling water =99oC
-final temperature of water, calorimeter and metal =23.7oC
-mass of cold water plus calorimeter =130g
-mass of calorimeter =50g
Take s.h.c. of water=4200JKg-1K-1, s.h.c. of copper=400JKg-1K-1.
Use the data above to determine:- The heat gained by the water and calorimeter
Q = mcΔθw + mcΔθc = (0.08 × 4200 × 3.7) + (0.05 × 400 × 3.7)
= 2741.2J - The specific heat capacity of the metal
0.1×c×71.3=2741.2
C=2741.2/0.1×71.3 = 381.46JKg-1K-1 - State the possible sources of error in the value of the s.h.c obtained in the above experiment.
- Heat loss as the metal was being transferred from the boiling water to the calorimeter.
- Error when reading the thermometer (parallax error)
- The heat gained by the water and calorimeter
- 3kg of hot water was added to 9kg of cold water at 10oC and the resulting temperature was 20oC. Ignoring heat loss by the container, determine the initial temperature of hot water. Take s.h.c of water=4200JKg-1K-1 .
mcΔθ h =mcΔθ c
3 × (θ-20) = 9 × 10
3θ=90+60 =150
θ = 150/3 = 50oC
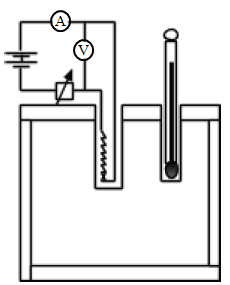
Electrical method
- Specific heat capacity of a solid
In this method, two holes are drilled in the solid to accommodate the heater and thermometer.
The solid is heated electrically for a given time.
Below is an arrangement that can be used:
In this method, the following data is recorded:
- Mass of the metal (solid)
- Heater voltage, V
- Heater current, I
- Time (duration) of heating, t
- Initial temperature of the solid
- Final temperature of the solid
The electrical energy lost by the heater is given by; E = VIt
Suppose there is no heat loss to the surroundings, then the heat lost by the heater equal heat gained the solid. i.e. VIt = mcΔθ
Hence c = VIt/mΔθ
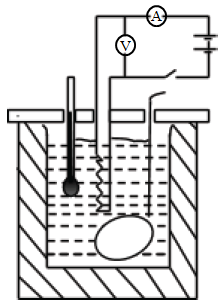
Note: Heat loss is minimized by lagging the calorimeter as well as oiling the holes. - Specific heat capacity of a liquid
The heat lost by the heater equal the heat gained by the liquid and the calorimeter.
VIt = mcΔθl + mcΔθc
Hence cl = (VIt – mcΔθc)/mΔθl
Example 7.2
- An immersion heater rated 120W, 240V is connected to a 240V power supply. How long will it take to heat 1 kg of water from 2 0 C to 90 0 C?
Take s.h.c of water=4200JKg-1K-1.
t = mcΔθ/VI = mcΔθ/P
t = (1 × 4200 × 80)/120 =2800seconds. - A heater rated 180W and a thermometer were inserted in a 0.5kg of water in a copper calorimeter. The following results were recorded:
Temperature, T (oC) 30 36 40 45 49 54 57 Time, t (minutes) 3 4 5 6 7 8 9 - Plot a graph of temperature against time
- Use the graph to find:
- The room temperature
- The specific heat capacity of water.
- A 180W heater is immersed in a copper calorimeter of mass 20g containing 200g of alcohol. When the heater is switched on, after 36 seconds the temperature of the calorimeter and its contents was raised by 12oC. Find the specific heat capacity of alcohol. Take the s.h.c of copper=400JKg-1K-1 .
Pt=mcΔθa + mcΔθc
Ca = (pt − mcΔθc )/mΔθa = (180× 36 − 0.1 × 400 × 12)/0.2 × 12
= 2500JKg-1K-1

Change of State
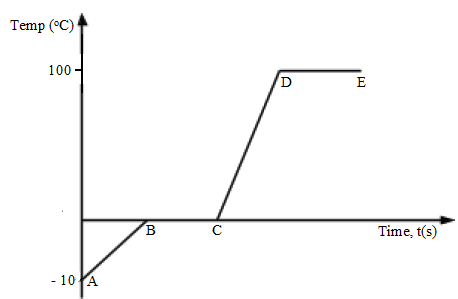
- When ice is heated say from -2oC until it boils, it undergoes changes which can be represented by the heating curve below:
- Between the points AB, ice absorbs heat energy and its temperature rises.
- Between BC, the ice absorbs its latent heat of fusion which it uses to melt. This change of state occurs at a constant temperature.
- Between CD water absorbs heat energy as its temperature rises until boiling point.
- As the water boils at constant temperature, it absorbs its latent heat of vaporization.
- When the vapour condenses to liquid, it gives out its latent heat of vaporization. Similarly, when a liquid freezes to solid, it gives out its latent heat of fusion.
Latent Heat of Fusion
- it is the quantity of heat needed to convert a given mass of a solid to liquid at constant temperature.
Specific Latent Heat of Fusion
- it is the quantity of heat needed to convert a unit mass of a solid to liquid at constant temperature. i.e. lf = Q/m
- Therefore Q=mlf
The SI unit of the specific latent heat of fusion is the joule per kilogram (JKg-1). - A unit mass of a substance changing from liquid to solid will give out heat energy equivalent to its specific latent heat of fusion.
Determination of specific latent heat of fusion.
There are two methods used:
- Mixture method
A piece of dry ice is dropped into a calorimeter containing water slightly above room temperature. Stir the mixture until all the ice has melted.
Suppose there is no heat loss to the surroundings, then the heat energy lost by the water and calorimeter equals the heat energy gained by the melting ice
In the above experiment, the following data is recorded for purposes of determining the specific latent heat of fusion:
-Mass of the dry ice
-mass of the water in the calorimeter
-mass of the calorimeter plus stirrer
-Temperature change of the water
Hence mcΔθw + mcΔθc = mlf
Lf = (mcΔθw + mcΔθc)/mi
Note: Dry ice is used due to its low moisture content. This implies that all the heat absorbed by the ice is used to melt the ice and not warming the moisture. - Electrical method
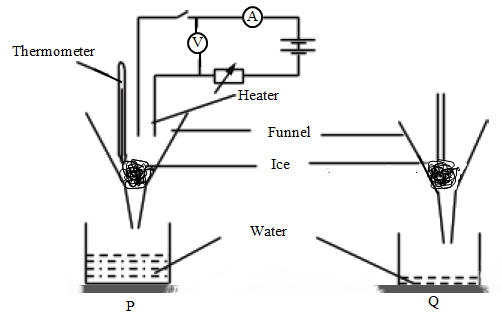
Equal amounts of crushed ice are put simultaneously in two identical filter funnels.
A heater is then immersed in the funnel in set up P .
Place clean dry beakers below each funnel.
Wait until a reasonable amount of water has collected in the beaker P then switch off the heater and remove the beakers.
Weigh the beakers and their contents.
In the above experiment, the following data is collected:
- Mass of the beaker under P before experiment, m1
- Mass of the beaker under P after the experiment, m2
- Mass of beaker under Q before experiment, m3
- Mass of beaker under Q after experiment, m4
- Heater voltage, V
- Heater current, I
- Duration of heating, t
Calculations
Mass of melted ice in set up P, mp = m2 − m1
Mass of melted ice in set up Q , mq = m4 − m3
Set up Q is called the control experiment. It helps to determine the mass of ice that melted as a result of the temperature of the room during the experiment.
In order to obtain the mass of ice melted by the heater only, it is important to subtract the mass of melted ice in Q from that melted in P;
i.e. m= mp − mq .
Then, heat energy supplied by the heater = heat energy absorbed by the melting ice.
VIt= mlf
Hence lf = VIt/m
The table below gives some common solids and their specific latent heats of fusion:
Material s.l.h of fusion (×105 ) JKg-1 Copper 1.0 Aluminium 3.9 Water (Ice) 3.34 Iron 5.7 Wax 1.8 Naphthalene 1.5 Solder 0.7 Lead 0.026 Mercury 0.013
Example 7.3
- A block of ice of mass 40g at 0oC is placed in a calorimeter containing 400g of water at 20oC. Ignoring heat absorbed by the calorimeter, determine the final temperature of the mixture after all the ice has melted. Take s.h.c.of water= 4200JKg-1K-1 and the s.l.h. of fusion of ice= 340, 000JKg-1 .
Heat lost by the hot water= heat gained by melting ice + heat gained by melted ice
mcΔθh = mlf + mcΔθm
0.4 × 4200 × (20 − θ) = (0.04 × 340, 000) + (0.04 × 4200 × θ)
33600 − 380θ = 13600 + 38θ
1848θ=20000
θ = 20000/1848 =5.82oC - 3g of dry ice was added to 20g of water at 26oC in a beaker of negligible heat capacity. After the ice had all melted, the temperature of water was found to be 12oC. Find the specific latent heat of fusion of ice. Taken the s.h.c of water = 4200JKg-1K-1 .
0.1 × 4200 × (26 × 11) = (0.03 × lf) + (0.03 × 4200 × 11)
6300=0.03lf + 737.2
Lf =5560.8/0.03 = 3.4755 × 25JKg-1 - An aluminium tray of mass 400g containing 300g of water is placed in a refrigerator. After 80 minutes, the tray is removed and it is found that 60g of water remains unfrozen at 0oC. If the initial temperature of the tray and its contents was 20oC, determine the average amount of heat removed per minute by the refrigerator. Take s.h.c of aluminium = 900JKg-1K-1, s.h.c of water = 4200JKg-1K-1, s.l.h. of fusion of ice = 3.4 × 105JKg-1 .
Solution
Heat lost by tray = mcΔθ = 0.4 × 900 × (20 − 0)= 7200J
Heat lost by water = mcΔθ= 0.3 × 4200 × 20 = 25, 200J
Latent heat of ice given out = mlf = (0.3-0.06) × 340, 000 = 999, 600J
Total heat energy absorbed by the refrigerator =3600 + 25200 + 999600 = 114000J
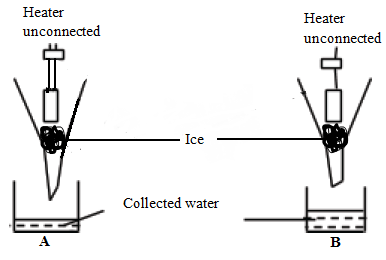
Hence amount of heat removed per minute = 114000J/80min = 1425J/min - In an experiment to determine the specific latent heat of fusion of ice, the following set up was used:
In A the heater is unconnected and when the ice is melting steadily, 0.015kg of water is collected in 300s. In B the is connected to a power supply rated 50W. When water drips at a steady rate, 0.058kg of water is collected in 300s. Calculate the value for the specific latent heat of fusion of ice.
Q= Pt = mlf
Lf = (50 × 300)/(0.058-0.015)
= 348, 833.21 JKg-1
Latent Heat of Vaporization
- This is the quantity of heat energy required to convert a given mass of a liquid to gas at constant temperature.
Specific Latent Heat of Vaporization
- This is the quantity of heat energy required to convert a unit mass of a liquid to gas at constant temperature.
Lv = Q/m
Therefore, Q= mlv - The SI unit of specific latent heat of vaporization is the joule per kilogram (JKg-1 ).
Determination of the specific latent heat of vaporization
Experiment
Aim: To determine the specific latent heat of vaporization of water using mixture method .
Apparatus
- Calorimeter with a stirrer
- Water
- Thermometer
- Flask with a delivery tube
- Heat source
- Weighing machine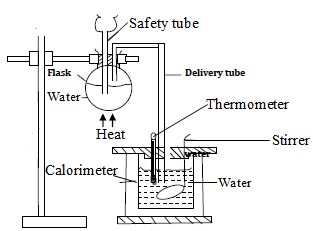
Procedure
- Set up the apparatus as shown above.
- Find the mass of the calorimeter when empty and when filled with water to the level shown.
- Measure and record the initial temperature of water in the calorimeter.
- Heat the water in the flask until it delivers steam through the delivery tube. Ensure that the free end of the delivery tube is inside water in the calorimeter.
- Allow steam to bubble into the water while stirring until the temperature of water rises by about 200C above the room temperature.
- Remove the delivery tube from the calorimeter and record the temperature of the water.
- Determine the new mass of the calorimeter and its contents. Hence, determine the mass of the condensed steam.
Note
Steam first condenses to water which then cools down, losing heat energy.
Therefore, heat energy lost by steam and the cooling water equal to the heat energy gained by the water and calorimeter.
mlv + mcΔθh = mcΔθw + mcΔθc
Lv = (mcΔθw+ mcΔθc −mcΔθh)/m
It is important to first cool the water in the calorimeter to a certain value below the room temperature and then pass the steam through it until the temperature rises above the room temperature by the same value. This will help minimize errors due to the heat loss to the surrounding.
Specific latent heat of vaporization using the electrical method
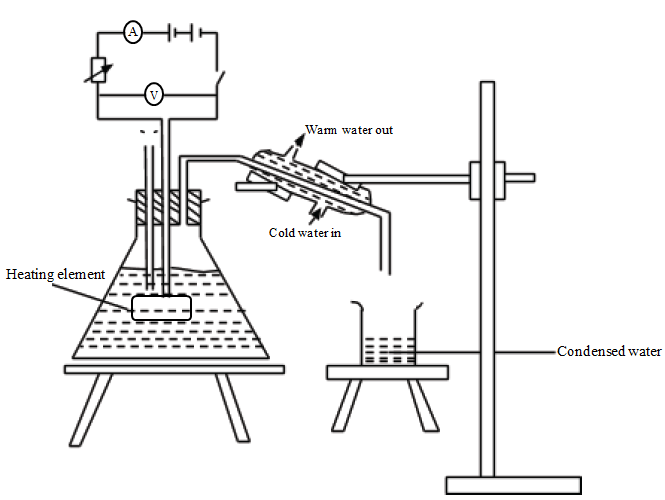
- The heating process is allowed to continue until a steady state where condensed water drips out at a constant rate has been achieved.
- The mass of water collected after a time, t is measured.
- The following data is collected in this experiment:
- Heater current, I
- Heater voltage, V
- Mass of empty beaker
- Mass of beaker and collected water
- Time taken to collect the condensed water
Suppose all the heat given by the heater is used to convert water to steam, then:
VIt = mlv
Hence, lv = VIt/m
The table below shows some common liquids and their specific latent heats of vaporization;
Liquid s.l.h. of vaporization × 105 (JKg-1) Water 3.6 Alcohol 6.6 Ethanol 6.5 Petrol 5.3 Benzene 1.0 Ether 3.5 Turpentine 5.7

Boiling and Melting
- Boiling and melting points are generally affected by two factors; impurities and pressure.
Melting
Effects of pressure on the melting point
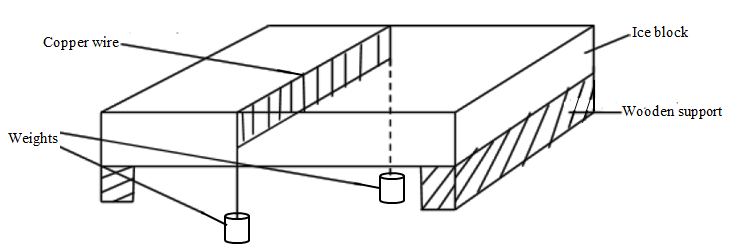
- Increase in pressure lowers the melting point of a material.
- This can be illustrated by suspending two weights supported by a copper wire on the surface of an ice block as shown below:
- The wire is seen to cut its way through the block of ice but leaves it as one piece. The suspended weights make the copper wire to exert pressure on the ice directly underneath which is made to melt at a temperature below its melting point. As the wire cuts through, the water formed flows over the wire and immediately solidifies since it is no longer under pressure. As the water solidifies, it gives out its latent heat of fusion which is conducted by the copper wire to melt the ice below it. This continues until the copper wire completely cuts through the ice leaving it intact.
- Note that copper wire has been used due to its high thermal conductivity. If a poor thermal conductor like cotton string was used, it would not cut through the ice block.
- The process by which water refreezes is referred to as regelation.
- The effects of high pressure on the melting point are applicable in ice skating and joining two pieces of ice blocks together.
- The weight of the skater acts on the thin blades of the skates exerting high pressure on the ice. The ice underneath thus melts, forming a thin film of water over which the skater slides.
- When two ice cubes are pressed hard against each, the high pressure between them lowers the melting point of the ice at the point of contact.
- When the pressing force is withdrawn, water recondenses and the two cubes are joined together.
The presence of impurities lowers the melting point of a material.
This is the reason behind spreading salt on roads and paths during winter in cold regions. This will prevent freezing on the roads.
Boiling
Generally:
- The presence of impurities in a liquid raises the boiling point of the liquid.
- An increase in pressure raises the boiling point of the liquid.
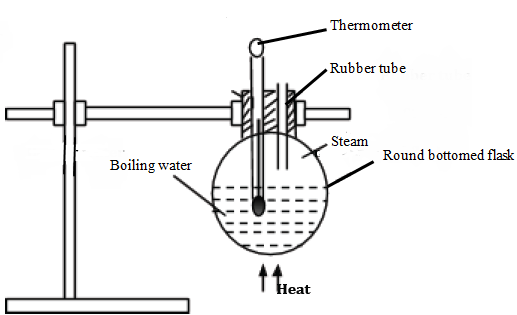
- The effects of pressure on boiling point may be illustrated by the set ups below:
Effects of increased pressure on boiling point
- The heating is done until water starts to boil. The temperature at which water boils is noted.
- When the rubber tube issuing steam is squeezed momentarily, the reading on the thermometer is observed to rise and boiling reduces.
- Note that closing the tube raises the vapour pressure within the flask.
- This makes it difficult for the molecules from the surface of the liquid to escape, raising the boiling point of the liquid.
- The effect of high pressure on boiling point is applied in a pressure cooker. Here the pressure is raised which raises the boiling point of water hence the food is cooked at a higher temperature.
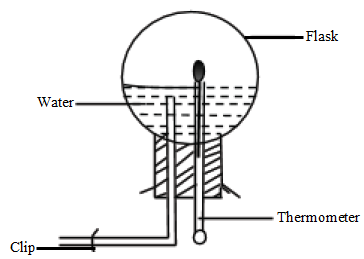
Effects of reduced pressure on boiling point
- Water is first heated to boiling. The flask is then turned upside down and cold water poured over it. It would be observed that when heating stops, boiling also stops.
- When cold water is poured over the flask, the water inside the flask begins boiling again although its temperature is below the boiling point.
- The cold water condenses the steam reducing vapour pressure inside in the flask. Hence a decrease in pressure lowers the boiling point of a liquid.

Boiling and Evaporation
- When a liquid is heated, the molecules close to the surface may gain sufficient kinetic energy to break away from the forces of attraction between the neighboring molecules and escape. This is called evaporation.
- Evaporation takes place at any temperature, even below the boiling point of the liquid.
Factors Affecting Rate of Evaporation
- Temperature
Increase in temperature of the liquid enhances evaporation. This is why clothes dry faster on a hot day. - Surface area
When the surface area is increased, the molecules of the liquid have greater chance of escaping. Hence a wet cloth would dry faster when it is spread out than when it is folded. - Humidity
When there is high amount of water vapour in the atmosphere, it becomes difficult for the molecules to escape.
This is why clothes take longer to dry on a humid day. - Draught/moving wind
Moving air above the surface of the liquid sweeps away the escaping molecules. Thus evaporation is enhanced by the passing air.
Differences Between Boiling and Evaporation
| Evaporation | Boiling |
| Occurs at all temperatures | Occurs at a fixed temperature |
| Occurs at the surface of the liquid | Take place throughout the liquid |
| No bubbles are formed | Bubbles are formed in the liquid |
| Decrease in atmospheric pressure increases the rate of evaporation | Decrease in atmospheric pressure lowers the boiling point if the liquid |
- Evaporation has a cooling effect which is applied in sweating in human beings and animals, cooling of water in porous pots and the refrigerator.
When water evaporates, it absorbs the latent heat from the body causing a cooling effect. - Different animals have different ways by which they cool their bodies. For instance, dogs expose their tongues when it is hot while the muzzle of a cow becomes more wet when it is hot. Both these are to increase the rate of evaporation thereby cooling the body.
- A porous pot has tiny holes which allow water to seep out slowly. As the water evaporates, it absorbs the latent heat causing a cooling effect.
Download QUANTITY OF HEAT - Form 3 Physics Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students