Introduction
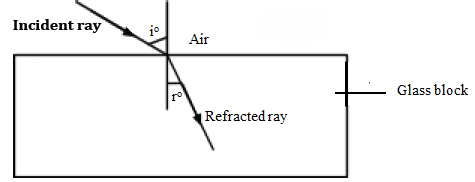
- Refraction refers to the bending of light when it passes from one medium into another of different optical density.
- This is because as light passes through different media its velocity changes.
- The bending occurs at the boundary or interface of the two media.
- The refracted ray may bend away or towards the normal depending on the optical density of the second medium with respect to the first medium.
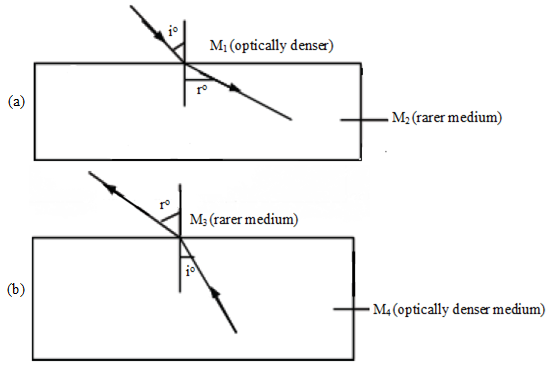
- Generally, a ray passing from an optically denser medium into a less optically dense (rarer) medium is bent away from the normal after refraction.
- If the ray passes from a rarer medium into an optically denser medium then it is bent towards the normal.
- It is easier to tell which medium is optically denser by simply comparing the angle between the incident ray and the normal and that between the refracted ray and the normal.
- The medium with a smaller angle (of incidence or refraction) is the optically denser medium.
- However, when the ray strikes the interface perpendicularly (normally) it passes undeviated (without bending). This is because the angle of incidence is zero.
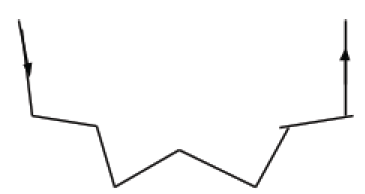
- In figure (b) above, only the direction of the light has been reversed leaving the angles the same. However, i now becomes r while r becomes i. The principle that makes it possible to reverse the direction of light keeping the sizes of the angles the rays make with the normal the same is called the principle of reversibility of light.
- The study of refraction of light helps us understand the following common phenomena:
- Why a stick appears bent when part of it is in water.
- Why a coin at the base of a beaker of water appears nearer the surface than it actually is.
- Why the stars twinkle.
- Why the sun can still be seen sometimes before it rises or even after setting.
- Why the summer sky appears blue.
- The formation of the rainbow.

Refraction in Glass
This can be investigated by the following steps:
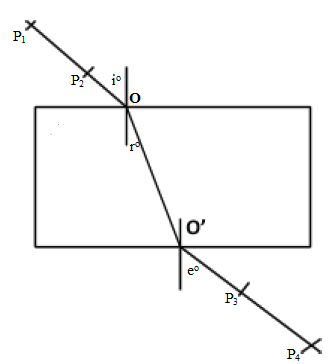
- Fix a white plain paper on a soft board using drawing pins. Place the glass block with its larger surface on the plain paper and trace its outline.
- Remove the glass block and then draw a normal through point O. Draw a line making an angle say i = 30o with the normal as shown above.
- Replace the glass block onto the outline and stick two pins P1 and P2 along the line such that they are upright and about 6cm apart.
- From the opposite side of the block, view the two pins and stick two pins P3 and P4 such that the four pins appear on a straight line. Join the positions of P3 and P4 using a straight line and produce the line to meet the outline at O’.
- Draw another normal at O’ and then join O to O’. Measure angles r and e .
- Repeat the above steps for other values of i=40o, 50o and 60o . Complete the table below:
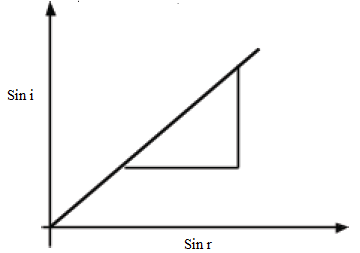
Angle of incidence, io 30o 40o 50o 60o Angle of refraction, ro eo Sin i Sin r Sin i/sin r - Plot a graph of Sin i against Sin r. determine the slope of your graph.
Observations
- The ratio of Sin i to Sin r is a constant.
- The graph of Sin i against Sin r is a straight line through the origin.
- The slope of the graph is equal to the ratio of Sin i to Sin r in the table.

The Laws of Refraction and Refractive Index
There are two laws of refraction:
- The incident ray, refracted ray and the normal at the point of incidence all lie in the same plane.
- Snell’s law : it states that the ratio of sine of angle of incidence to the sine of angle of refraction is a constant for a given pair of media.
i.e. Sin i/Sin r = a constant.
The constant is referred to as the refractive index, η of the second medium with respect to the first medium.
The first medium is that medium in which the incident ray is found while the second medium is that medium where the refracted ray is found. It is denoted as 1η2.
Hence in the previous section, the ratio Sin i/Sin r is the refractive index of glass with respect to the air since the light passed from air into glass block.
However, when light passes from vacuum into another medium, it is referred to as absolute refractive index.
Therefore for absolute refractive index, the angle of incidence i is found in a vacuum.
i.e. absolute refractive index= sin i(in vacuum)/sin r(in the second medium).
Recall:
1η2 =sin i/sin r
By the principle of reversibility of light, r now becomes i and i becomes r i.e. the incident ray is now found in the second medium.
Hence 2η1 =sin r/sin i
But sin r/sin i=1/(sin i/sin r)=1/1η2
Therefore 2η1 =1/1η2.
The table below shows some materials and their refractive indices:
Note that the refractive indices given in the above table are with respect to air i.e. when light travels from air into the various media.Material Refractive index Ice 1.31 Crown Glass 1.50 Water 1.33 Alcohol 1.36 Kerosene 1.44 Diamond 8.42
Example 8.1
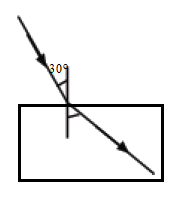
- In the figure below, calculate the angle of refraction r given that the refractive index of the glass is 1.50.
By the principle of reversibility of light;
sin r/sin 30o = 1.50
sin r = 1.50 × sin 30o
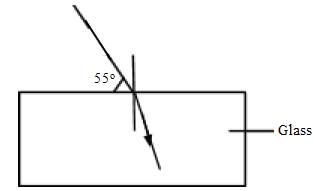
r = sin-1(1.50 × sin 30o)= 48.6o - A ray of light is incident on a flat glass surface as shown below:
Given that the refractive index of glass is 1.50, determine the angle of refraction for the ray of light.
1.50 = sin 35/sin r
Sin r = sin 35/1.50
r=sin-1(sin 35/1.50) = 3.48o
Refraction through Successive Media
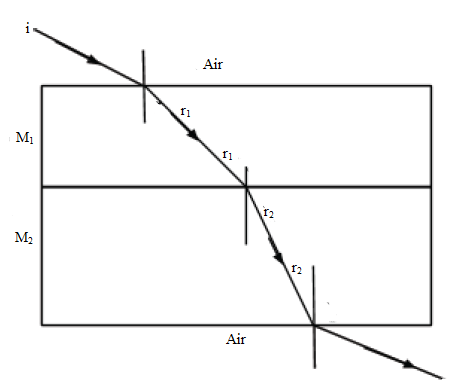
- Consider a ray of light passing through a series of media as shown below:
- Suppose the boundaries are parallel, then:
aη1 =sin i/sin r1………………………………. (i)
1η2 =sin r1/sin r2 …………………………… (ii)
2ηa =sin r2/sin i ……………………………… (iii) - By the principle of reversibility of light;
aη2 =sin i/sin r2……………………………. (iv) - Also, multiplying equations (i) and (ii), we get:
aη1 × 1η2 = sin i/sin r1 × sin r1/sin r2 = sin i/sin r2.
Thus aη2 = aη1 × 1η2. - Generally, 1ηk = 1η2 × 2η3 ×………….× k-1ηk .
Example 8.2
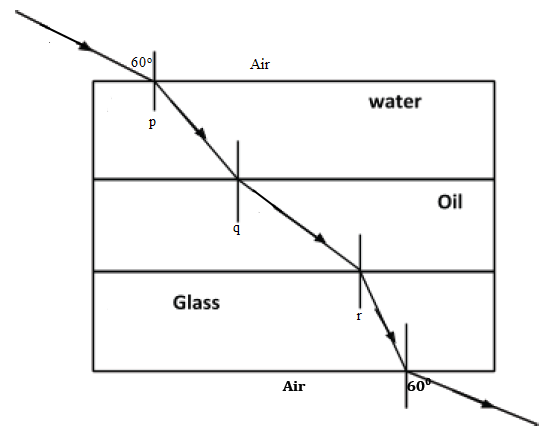
- A ray of light from air passes successively through parallel layers of water, oil, glass and then into air again. If the refractive indices of water, oil and glass are 4/3, 6/5 and 3/2 respectively and the angle of incidence in air is 60o .
- Draw a diagram to show how the ray passes through the multiple layers.
- Calculate:
- The angle of refraction in water.
4/3= sin 60/sin r
r=sin-1(3sin60/4)= 40.5o - The angle of incidence at the oil-glass interface.
oηg =sin q/sin r
By the principle of reversibility of light, aηg =sin 60/sin r = 3/2
r= sin-1(2sin 60/3) =38.27o .
Also, oηg = oηa × aηg =5/4
Therefore, 5/4= sin q/sin 38.27
q=sin-1(5sin38.27/4)=48.4o
- The angle of refraction in water.
- Draw a diagram to show how the ray passes through the multiple layers.
Refractive Index in terms of Real and Apparent Depth
- This is on the basis that when an object at the base of a container filled with water is viewed perpendicularly it appears closer to the surface than it actually is. Consider the figure below:
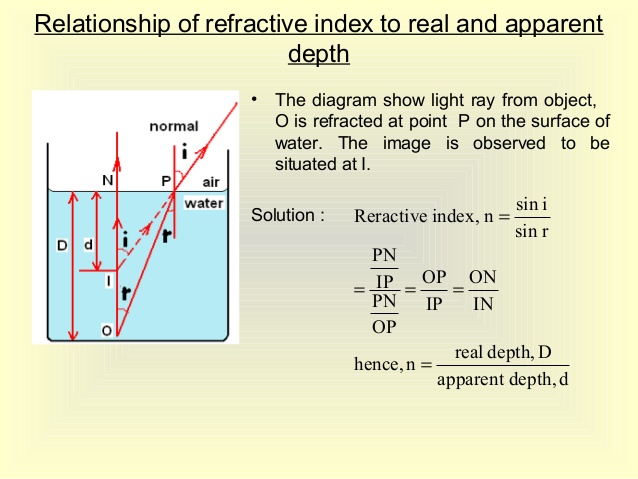
- Hence, refractive index of water= Real depth/Apparent depth.
- When a graph of real depth against apparent depth is plotted, the graph obtained is a straight line through the origin and whose gradient is equal to the refractive index of the medium involved.
Example 8.3
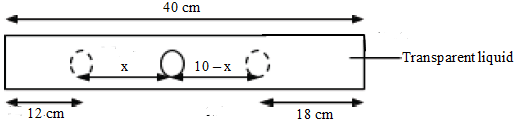
- In a transparent liquid container, an air bubble appears to be 12cm when viewed from one side and 18cm when viewed from the other side. If the length of the tank is 40cm, where exactly is the air bubble?
Refractive index of glass= (12+x)/12 = (18+2-x)/18
x= 20/5 = 4cm.
Therefore, the bubble is 3cm in the liquid from the left-hand side. - A microscope is focused on a mark on a horizontal surface. A rectangular glass block 30mm thick is placed on the mark. The microscope is then adjusted 2mm upwards to bring the mark back to focus. Determine the refractive index of the glass.
aηg =real depth/apparent depth= 30mm/20mm =1.50
Refractive Index in Terms of Velocity of Light
- Refraction occurs as a result of the different light velocity in different media. Basically, refractive index of any medium is the ratio of the velocity of light in a vacuum or air to the velocity of light in that medium; η m = velocity of light in vacuum/velocity of light in the medium.
Note that the velocity of light in a vacuum is 3.0 × 108 m/s.
Generally, 1η2 =velocity of light in medium 1/velocity of light in medium 2.
Example 8.4
- The velocity of light in glass is 8.0 × 108 m/s. Calculate:
- The refractive index of glass.
ηg = velocity of light in vacuum/velocity of light in glass= (3.0 × 108)/( 8.0 × 108 ) = 1.50 - The angle of refraction in glass for a ray of light incident at the air-glass interface at an angle of incidence of 40o.
Sin 40o/sin r =1.50
r = sin-1(sin40/1.50)= 10.4o.
- The refractive index of glass.
- Calculate the speed of light in diamond of refractive index 8.1.
ηd =velocity of light in vacuum/velocity of light in diamond
8.4= (3.0 × 108)/Vd
Vd =(3.0 × 108 )/8.4 =1.25 × 2 8 m/s. - The speed of light in medium 1 is 8.0 × 108 m/s and in medium 2 is 1.5 × 108 m/s. Calculate the refractive index of medium 2 with respect to medium 1.
1η2 =V1/V2 = (8.0 × 108 m/s)/(1.5 × 108 m/s)
=1.33
Total Internal Reflection, Critical Angle and Refractive index
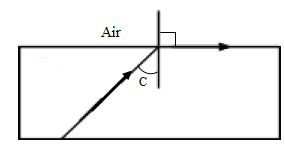
- As the angle of incidence in the denser medium increases the angle of refraction also increases. If this continues until the angle of refraction reaches 90o , the angle of incidence is called the critical angle C. A critical angle is defined as the angle of incidence in the denser medium for which the angle of refraction is 90o in the less dense medium.
- By the principle of the reversibility of light,
aηg = sin90/sin C =1/sin C. - If the angle of incidence exceeds the critical angle, the light undergoes total internal reflection. This reflection obeys all the laws of reflection.
- For total internal reflection to occur, two conditions must be satisfied, namely:
✓ Light must pass from an optically denser medium to a less optically dense medium.
✓ The angle of incidence in the denser medium must be greater than the critical angle.
Example 8.5
- Calculate the critical angle for glass whose refractive index is 1.50.
1.50= 1/sin C.
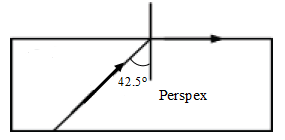
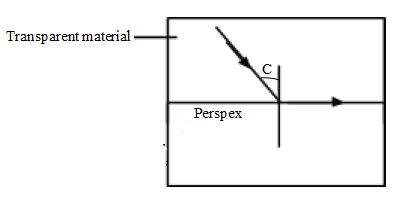
C = sin-1(1/1.50) = 41.8o - The figure below shows the path of a ray light passing through a rectangular block of Perspex placed in air.
- Calculate the refractive index of Perspex.
aηp =1/sin48.5 = 1.48 - A ray of light now travels from a transparent medium of refractive index 8.4 into the Perspex as shown below:
Calculate the critical angle C.
pηm = sin C/sin 90o= pηa × aηm =(1/aηp) × aηm
=1/8.4 × 1.48=1.48/8.4
C= sin-1(1.48sin90/8.4) =38.07o.
- Calculate the refractive index of Perspex.
Effects of Total Internal Reflection
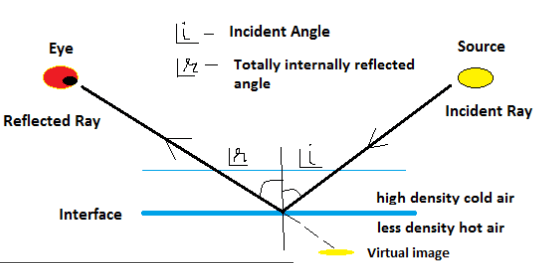
- Mirage
On a hot day, the air above the ground is at a higher temperature than the layers above it. Thus the density of air increases with height above the ground. Denser air is optically denser than lighter one. Hence, a ray of light from the sun undergoes continuous refraction at the boundaries between any two layers of air with different temperatures. In each case, the ray bends away from the normal until the critical angle is achieved. Thereafter, the ray undergoes total internal reflection. An inverted image in the form of a pool of water is observed. This phenomenon is referred to as mirage.
Generally, mirage occurs as a result of continuous and progressive refraction at the air boundaries and total internal reflection. Mirage also occurs in cold regions but this time the ray of light curves upwards. - Atmospheric refraction
The sun is sometimes seen before it actually rises or after it has set. This is because the light from the sun is refracted by the atmosphere towards the earth. (Recall: the earth is spherical).
Applications of Total Internal Reflection
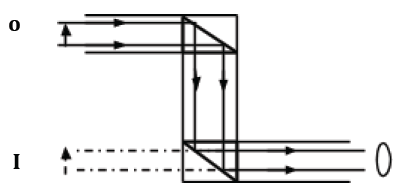
- A prism periscope
It makes use of two right-angled isosceles prisms. The light from the object is inverted through 90 0 by the first prism and a further 90 0 by the second prism.
This periscope produces brighter images compared to those of the simple periscope in which a plane is used. The image formed is erect and virtual. A prism periscope has the following advantages over the simple periscope:
✓ Forms brighter and clearer images. A simple periscope produces many faint images besides the main image especially if the mirror is thick.
✓ Does not absorb the energy of the light. Plane mirrors absorb some light incident on them.
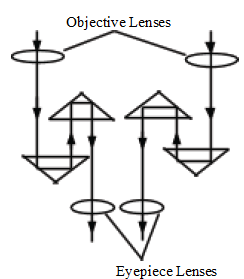
✓ Has a tough structure and thus does not easily wear. The painting on the plane mirror can wear out with time. - A prism binoculars
This device is used to reduce the distance between the eyepiece and the objective thereby reducing the length of the telescope. It forms an erect image. - Optical fibre
It is a thin flexible glass rod made up of two parts; the inner part made of glass of higher refractive index and the outer glass coating of lower refractive index. When a ray of light enters the fibre at an angle greater than the critical angle, it undergoes a series of total internal reflection before it finally emerges from the other end. None of the light energy is lost in the process.
Optical fibres are used in medicine for viewing internal body organs (the endoscope) as well as in telecommunication. They are preferred to ordinary cables because they are light and thin and do not cause scattering of the signals.

Dispersion of Light
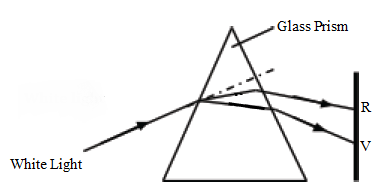
- White light from the sun is made up of seven colours. They all travel with the same velocity in vacuum but their velocities vary in other transparent media like glass and water.
- Hence when a ray of white light travels from a vacuum into a glass prism, it is separated into its component colours ranging from red, orange, yellow, green, blue, indigo to violet. The spreading out of light into its constituent colours by another medium is called dispersion .
- Pure light is called monochromatic light while an impure light like white light is referred to as non-monochromatic or composite light.
- Dispersion of light is illustrated by the diagram below:
- Red is least deviated while violet is the most deviated ray. Hence red light has the greatest velocity and violet the least velocity in glass.
- The coloured band produced is called a visible spectrum.
- The spectrum produced above is impure. In order to obtain a pure spectrum where each colour is distinct, an achromatic lens is placed between the screen and the prism.
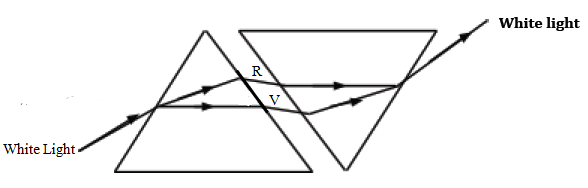
- When the seven sevencolours are recombined, a white light is obtained. This can be achieved by using a similar but an inverted prism.
The Rainbow
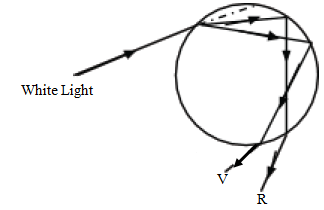
- When a ray of light passes through a water drop, a rainbow is produced. The water disperses the light into its constituent colours.
- Each colour then undergoes total internal reflection within the drop before it eventually emerges into air again.
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download REFRACTION OF LIGHT - Form 3 Physics Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students