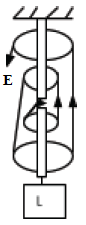Work and Energy
- When a force acting on a body displaces the body in the direction of the force work is said to have been done.
- Work is the product of force and displacement in the direction of the force;
Workdone= force F × displacement s. - The SI Unit of work is newton-metre (Nm).
1Nm= 1joule (1J). - A joule is defined as the workdone by a force of one newton to displace a body through one metre in the direction of the force.
- Other multiples of the joule include kilojoule(kJ) and megajoule(MJ).
- Energy on the other hand is the ability or capacity to do work. Anything that possesses energy is capable of doing work.
- The SI Unit of energy is the joule.
- Energy has the following characteristics:
- It is not visible.
- Occupies no space.
- Has no mass nor any other physical property.
- The most common sources of energy include the sun, wind, geothermal, waterfalls, nuclear or atomic energy, fuels etc.
- Energy resources may be grouped into two:
- Renewable energy- can be reused again and again. Their supplies are inexhaustible e.g solar, geothermal, wind energy.
- Non-renewable energy- their supplies are exhaustible i.e. cannot be reused once exhausted e.g. wood, coal biogas, petroleum etc.
- Energy exists in many forms such as mechanical, chemical, heat and electrical energy amongst others. In this topic, we will look at mechanical energy.
Mechanical Energy
- It is divided into two areas namely kinetic energy and potential energy.
- Kinetic energy is the energy possessed by a body in motion. Suppose a body of mass m is moving with a constant velocity v, then its kinetic energy is given by;
Kinetic energy=½(mv2 ). - Potential energy on the other hand is a form of stored energy in a body when it is in a particular state or position.
- A body in a raised position possesses gravitational potential energy given by;
P.Eg =mgh , where m- mass of the body, g- gravitational field strength and h- height above the ground. - Also, a stretched or compressed material is able to regain its original shape when released.
- This is because it possesses a type of potential energy known as elastic potential energy . As can be recalled from Hooke’s law, the workdone in stretching or compressing an elastic material is given by;
W=½(Fe) =½(ke2 ).
Hence the elastic potential energy is given by;
P.Ee =½(Fe) =½(ke2 ).
The Law of Conservation of Energy
- The law states: energy can neither be created nor destroyed but can be transformed from one form to another.
- Alternative statement: the sum of kinetic energy and potential energy of a system is a constant.
- Below is the energy transformation in a hydroelectric power station:
Example 3.1
- A force of 40N is applied on a body. The body moves a horizontal distance of 7m. Calculate the workdone on the body.
W = F × s = 40N × 7m
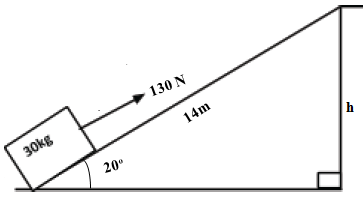
=280Nm or 280J - A box of mass 30kg is pushed up an inclined plane of length 14m using a force of 130N as shown below:
If the track is inclined at an angle of 200 , calculate:- The height of the platform.
Sin 20o =h/14
h=14sin 20o = 12.78 m - Workdone by the force of 130N.
W=F × s = 130 × 14 = 1820J - Workdone, if the box is lifted vertically upwards. Compare your answer in (b) and (c) above.
W = mgh = 300sin 20o = 273.88 J
Workdone in pushing the body along the inclined plane is greater than the workdone when lifting the body vertically upwards. This is because of the frictional force between the body and the inclined plane. - The frictional force between the box and the inclined plane.
Fr =1820−300sin 20o =1546.11 N
- The height of the platform.
- A crane is used to lift a body of mass 30kg through a vertical distance of 5.0m.
- How much work is done on the body?
W = F × s = (mg)s= 300 × 6=1800J - What is the potential energy stored in the body?
P.E = mgh=30 × 10 × 6 = 1800J - Comment on the two answers above.
Workdone on the body is equal to the potential energy stored in the body. Hence the workdone against gravity is stored as the potential energy.
- How much work is done on the body?
- A spring of spring constant 25N/m is stretched such that its length increases from 2cm to 20cm. calculate the amount of workdone on stretching the spring.
W=½(ke2) = ½(25)(0.182).
=0.405J - A body of mass 12kg is pulled from the rest with a constant force of 25N. The force is applied for 5.0s. Calculate:
- The distance travelled.
F=ma
a=25N/12kg =2.083 m/s2 , u=0, t=5
s=ut+½at2 =(0×6)+½(2.083)(52 ) = 26.0375 m - Work done on the body.
W=F×s = 25 × 26.0375 =650.9375 J - The final kinetic energy of the body.
K.E=workdone= 650.9375 J - The final velocity of the body.
K.E=½(mv2) = 650.9375 J
v={(2 × 650.9375)/12}½ = 10.416m/s.
- The distance travelled.

Power
- Power is defined as the rate of doing work;
Power=workdone/time. - The SI Unit of power is the watt (W).
1W= 1 J/s. - Other multiples of the watt include the kilowatt(kW) and megawatt(MW);
1W=10-3 kW
1W=10-6 MW - The power of a device is the measure of how fast the device can perform a given task or convert a given amount of energy.
- For example, a device rated 1kW converts 200J of energy to another form in one second.
Power=workdone/time =Fd/t
But d/t =velocity v.
Therefore, power= force F × velocity v.
Example 3.2
- A person of mass 60kg climbs 3m up a rope in 20seconds. Find the average power developed by the person.
Power=workdone/time =(600×3)/20 = 90 W - A person of mass 40kg runs up a flight of 50stairs each of height 20cm in 5 seconds. Calculate:
- The workdone.
W=mgh=40×10×(50×0.2) = 4000 J - The average power of the person.
Power=4000 J/5s =800W - Explain why the energy the person actually uses to climb up is greater than the calculated workdone.
- The workdone.

Machines
- A machine is a device that makes work easier
- In a machine, a force applied at one point of a system is used to generate another force at a different point of the system to overcome a load.
- The following terms are used in machines:
- Effort
- the force applied to the machine.
- Load
- the force exerted by the machine.
- Mechanical advantage (M.A)
- the ratio of the load to effort.
- M.A=Load/Effort.
- It has no units.
- It is dependent on friction between the moving parts and the weight of the parts of the machine that have to be lifted when operating the machine; the greater the friction the smaller the mechanical advantage.
- Velocity ratio (V.R)
- it is defined as the ratio of the velocity of the effort to the velocity of the load;
- V.R = velocity of effort/velocity of load = Effort distance/time/Load distance/time
Thus V.R=effort distance/load distance.
Velocity ratio also has no units.
- Efficiency η
- It is the ratio of the workdone on the load (work output) to the workdone by the effort (work input) expressed as a percentage;
- Efficiency η= (work output/work input) × 100.
- Efficiency also depends on the friction between the moving parts and the weight of the moveable parts.
- Hence the efficiency of a machine is always less than 20%.
Efficiency=work output/work input= (load×load distance)/(effort×effort distance)
= (load/effort) × (load distance/effort distance)
But load/effort =mechanical advantage (M.A),
And, load distance/effort distance =1/velocity ratio
Therefore, efficiency η= (M.A/V.R)×100.
- Effort
Example 3.3
- A machine requires 6000J of energy to lift a mass of 55kg through a vertical distance of 8m. Calculate its efficiency.
Work input = 6000 J
Work output = F × s = 55 × 10 × 8 = 4400 J
Efficiency=(work output/work input) × 100 = (4400/6000) × 100 = 73.33% - An effort of 250N raises a load of 900N through 5m in a machine. If the effort moves through 25m, find:
- The useful workdone in raising the load.
Useful workdone=load×load distance =900×5= 4500 J - The workdone by the effort.
Workdone by the effort= effort × effort distance= 250 × 25= 6250 J - The efficiency of the machine.
Efficiency= (work ouput/work input) × 100= (4500/6250) × 100 = 72%.
- The useful workdone in raising the load.
- A machine whose velocity ratio is 8 is used to lift a load of 300N. The effort required is 60N. calculate:
- The mechanical advantage of the machine.
M.A= load/effort = 300/60 = 5 - The efficiency of the machine.
Efficiency= (M.A/V.R)×100= (5/8) × 100 = 62.5%
- The mechanical advantage of the machine.
Types of Machines
- Below are some of the common machines:
Inclined Plane
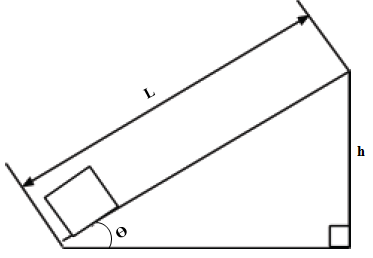
- The distance moved by the effort is L while the vertical height moved by the load is h.
Also, sin θ = h/L
Or simply h = L sinθ - Therefore, velocity ratio (V.R)= effort distance/load distance = L/L sin θ.
Hence V.R= 1/sin θ.
Example 3.4
- A man uses an inclined plane to lift a 81kg mass through a vertical height of 1.0m. Given that the angle of inclination of the plane is 300 and its efficiency is 75%, determine:
- The effort needed to move the load up the inclined plane at a constant velocity.
V.R=1/sin 30 = 2
Therefore, (M.A/2)×100=75
M.A= (2 × 75)/100 =3/2
3/2 = 82 N/effort
Effort= (82×2)/3 = 540N - The workdone against friction in raising the mass through the height of 1.0m.
Work input=effort×effort distance = (540×4)/sin 30 =4320J
Work output=load×load distance= 81×2×4= 3240J
Therefore, workdone against friction= 4320 − 3240= 1180J
- The effort needed to move the load up the inclined plane at a constant velocity.
A Screw and Bolt
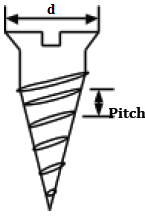
- For a screw, when the effort applied on the head moves through a complete revolution, the screw advances by a distance equivalent to one pitch.
- A pitch is the distance between two successive threads.
- Distance moved by the effort= circumference =πd
- Distance moved by the load= one pitch
- Hence, velocity ratio (V.R)= circumference/pitch =πd/pitch.
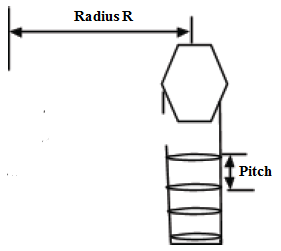
- For the bolt, effort is applied at the free end of the spanner.
- Therefore, the distance moved by the effort in one revolution= circumference= 2πR.
- Hence, V.R= circumference/pitch =2πR/pitch.
- Note that a combination of a screw and lever can be used as a jack for fitting heavy loads e.g car jack.
- When two or more systems are combined together, the overall velocity ratio is the product of the individual velocity ratios;
- Combined V.R= V.R1 × V.R2 ×………. ×V.Rk
Example 3.5
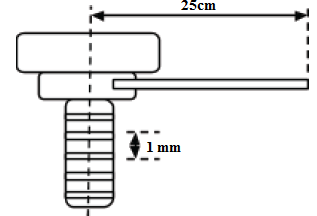
- The figure below shows a screw jack whose screw has a pitch of 1mm and has a handle of 25cm long
Determine the velocity ratio of the jack.
V.R= 2πr/pitch= 2π(25cm)/0.1cm= 1571
Lever System
- The velocity ratio of a lever system is the ratio of the effort arm to the load arm;
V.R= Effort arm/Load arm.
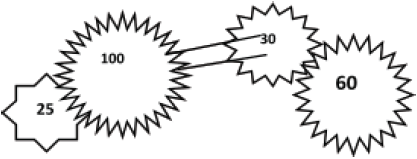
Gears
- A gear is a wheel with equally spaced teeth or cogs around it.
- The wheel on which the effort is applied is called the driving (input) gear while the load gear is referred to as the driven (output) gear.
- Suppose the driving gear has n teeth and the driven gear N teeth, then when the driving gear makes one complete revolution the driven gear makes n/N revolutions.
V.R of the system = Number of revolutions made by the effort (driving) gear/Number of revolutions made by the load (driven) gear.
V.R = 1revolution/n/N revolutions=N/n
Hence, velocity ratio of a gear system is the ratio of the number of teeth of the driven gear to the number of teeth of the driving gear; - V.R= Number of teeth of the driven gear/Number of teeth of the driving gear
Example 3.6
- A driving gear having 25 teeth engages with a second gear with 20 teeth. A third gear with 30 teeth on the same shaft as the second one engages with a fourth gear having 60teeth. Find:
- The total velocity ratio of the system.
Combined V.R=V.R1 × V.R2
V.R1 =No. of teeth of driven gear/No. of teeth of driving gear
= 20/25 = 0.8
V.R2 =60/30= 2Hence, V.R= 0.8×2= 1.6 - The mechanical advantage of the system if its efficiency is 85%.
Efficiency= (M.A/8)×100= 85
M.A= (85×8)/20= 5.8
- The total velocity ratio of the system.
Pulleys
- A pulley is a wheel with a groove to accommodate a string or rope. There are three possible systems of pulleys namely single fixed, single moveable and a block and tackle.
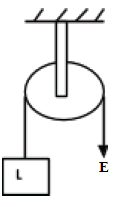
- Single fixed pulley
- In this arrangement, both the effort and load move through the same distance. Hence the velocity ratio of the system is one.
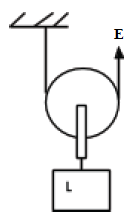
- Single moveable pulley
- The load is supported by two sections of the string. If the load is pulled upwards through a distance of 1m, each section of the string also moves through 1m. Hence the effort moves through a total distance of 2m. Therefore, the velocity ratio of the system = effort distance/load distance =2m/1m =5.
- A block and tackle
- This system comprises two sets; one set fixed and the other moveable. A single string is then passed around each pulley in turn.
- The arrangement can take several forms depending on the desired velocity ratio. Below is an
Example:
- Single fixed pulley
- In this case, there are four sections of the string supporting the load. Hence, when the load moves upwards through a distance of 1m, each section of the string also shortens by 1m. Therefore, the total distance moved by the effort (string) is 4m.
Thus, V.R of the system= effort distance/load distance =4m/1m = 4. - Coincidentally, the velocity ratio of the system is the same as the number of sections of the string supporting the load.
- Generally, the velocity ratio of a block and tackle system is given by the number of sections of the string supporting the load.
- Practically, the efficiency of any pulley system is less than 20%. This is as a result of two reasons:
- The friction between the moveable parts.
- The weight of the parts that have to be lifted when operating the system.
Example 3.7
- The figure below shows a pulley system used to raise a load
- State the velocity ratio of the system.
V.R=number of strings supporting the load= 6 - If an effort of 200N is needed to raise a load of 4500N, determine the efficiency of the system.
M.A= load/effort= 4500N/200N= 1.5
Efficiency = (M.A/V.R)×20= (1.5/6)×100= 75% - Calculate the wasted energy if a mass of 500kg is lifted up through a height of 2m using the same system.
Work ouput= load*load distance= 500×2×2= 2000J
Efficiency= (work output/work input)×20
Therefore, (2000J/work input)×100=75
Work input= (2000×20)/75 =13333.33J
Wasted energy= 13333.33×2000= 3333.33J
Alternatively, wasted energy=25% of work input= (25/20)×13333.33J=3333.33
- State the velocity ratio of the system.
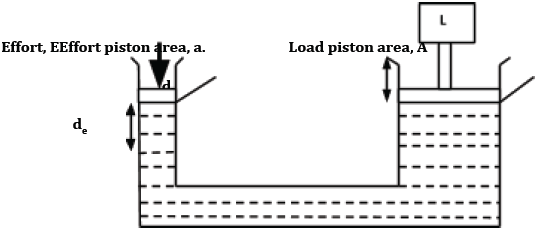
Hydraulic Machine
- Consider the diagram below:
- When the effort is applied as shown, the volume of the liquid leaving the effort arm is the same as the volume of the liquid entering the load arm;
i.e. a×de =A×dl ,
de/dl = A/a - Therefore, the velocity ratio of a hydraulic system is the ratio of the area of the load piston to the area of the effort piston. If the pistons are circular then;
V.R=area of load piston/area of effort piston =πR2 /πr2
V. =R2/r2 , where R- is the radius of the load piston and r- is the radius of the effort piston.
Example 3.8
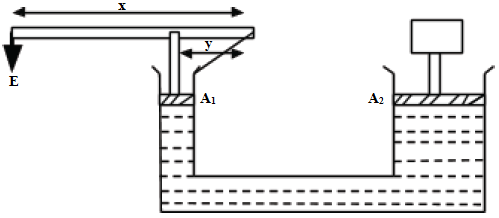
- In the figure below x=30cm, y=6cm, effort E=60N, A1 =4cm2 and A2 =12cm2.
Calculate:- The force F exerted on the liquid at A1 .
By the principle of moments;
60N×30cm= F×6cm
F= (60×30)/6= 300N - The velocity ratio of the system.
V.R of the lever system= effort arm/load arm =30cm/6cm= 5
V.R of the hydraulic system= area of load piston/area of effort piston= 12cm2/4cm2 = 3
Therefore, the combined V.R= 5×3= 15 - The maximum load that can be raised by the system.
Pressure at A 1 = Pressure at A2
300N/4cm2 =L/12cm2
L= (300×12)/4 =900N.
- The force F exerted on the liquid at A1 .
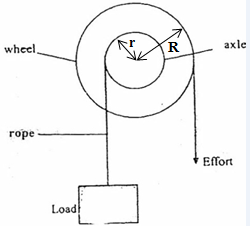
Wheel and Axle
- It consists of a large wheel of radius R attached to an axle of radius r
- Note that in this case, both the wheel and axle make the same number of revolutions at any time;
- Thus, in one revolution the distance moved by the effort= 2πR,
- And the distance moved by the load= 2πr.
- Hence, the velocity ratio of the system= 2πR/2πr = R/r.
- Thus the velocity ratio of a wheel and axle is the ratio of the radius of the wheel to the radius of the axle.
Example 3.9
- A wheel and axle is used to raise a load of 140N by a force of 20N applied to the brim of the wheel. If the radii of the wheel and axle are 70cm and 5cm respectively, Calculate the mechanical advantage, velocity ratio and efficiency of the system.
M.A= load/effort =140N/20N= 7
V.R =radius of the wheel/radius of the axle= 70cm/5cm= 14
Efficiency= (M.A/V.R)×100
= (7/14)×100= 50%
Pulley Belt
- This is where one wheel is used to drive another wheel by means of a belt.
- The driving wheel covers a distance 2πR in one revolution while the driven wheel covers a distance 2πr in one revolution.
- If the driving wheel makes one revolution, the driven wheel makes 2πR/2πr (R/r) revolutions.
V.R of the system= Number of revolutions made by the effort (driving) wheel/Number of revolutions made by the load (driven) wheel
V.R = 1/(R/r) =r/R
Therefore, the velocity ratio of a pulley belt is the ratio of the radius of the driven (load) wheel to the radius of the driving (effort) wheel.
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download WORK, ENERGY, POWER AND MACHINES - Form 3 Physics Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students