Whole Numbers - Grade 7 Mathematics Revision Notes

• Whole Numbers
  • Properties of Whole Numbers

Whole Numbers

All the positive numbers 1; 2; 3; 4; … are called the set of natural numbers. If we include 0 in the set of natural numbers, we get the set of counting numbers or whole numbers. We use numbers to add, subtract, multiply and divide. We can also write numbers in a particular order, from largest to smallest, e.g., 124; 1124; 5124; 9124. When we need to estimate, we can round off numbers to the nearest 5, 10, 100 or 1000. Whole numbers – or counting numbers are the numbers, 0; 1; 2; 3; 4; … and are represented by the symbol Nₒ.
Natural numbers – are whole numbers greater than or equal to 1: (1; 2; 3; 4; …) and are represented by the symbol N.

Rounding off to the nearest 5:
Look at the last digit of the number (the units digit) and round the number off to the closest number that 5 divides into.
1; 2 – “Move back to number ending in 0”
3; 4 – “Move forward to the number ending in 5”
6; 7 - “Move back to number ending in 5”
8; 9 - “Move forward to the number ending in 0”

Round off a number to the nearest 10:
When rounding off to the nearest 10, look at the units- digit.
Underline the Tens digit - 586
Look at the digit to the RIGHT of the Tens digit - 586
If this digit is 0, 1, 2, 3, or 4, the Tens stay the same. This is called rounding down. If this digit is 5, 6, 7, 8 or 9, round up. This is called rounding up.
586 rounded to the nearest 10 is 590.
We use the same method to round off to 100 (look at the tens digit) and 1000 (look at the hundreds digit)
For example: 465 784 rounded off to the nearest 10 is 465 780.
465 784 rounded to the nearest 100 is 465 800.
465 784 rounded to the nearest 1000 is 466 000.
Try this:
Round off 987 516 to:

1. The nearest 5
2. The nearest 10
3. The nearest 100
4. The nearest 1000

Properties Of Whole Numbers

Adding numbers is called finding the sum, and subtracting numbers is called finding the difference. Multiplying numbers is called finding the product and dividing numbers is called finding the quotient.
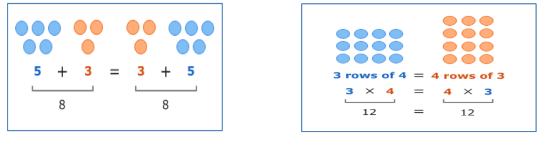
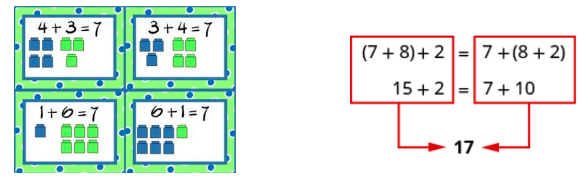
When you add or multiply numbers, the order of the numbers does not matter, for example: 4 + 5 = 5 + 4 and 4 x 5 = 5 x 4. This is called the commutative property of addition and multiplication.

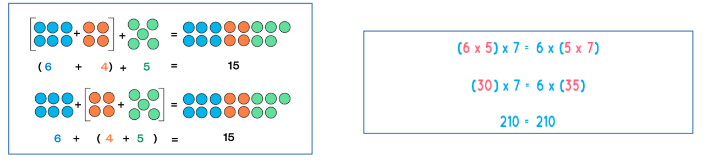
The order in which you add or multiply numbers also does not matter, for example: (4+5) +6 = 4 + (5+6) and (4x5) x6 = 4 x (5x6). This is called the associative property of addition and multiplication.

Distributive, Associative And Commutative Property

1. 2 x 5 + 2 x 6 – 2 x 7 
   = 2 x (5 + 6 - 7)
   = 2 x 4 
   = 8
2. 123 x 7
   =(100 + 20 + 3) x 7
   =(100 x 7)+(20 x 7)+(3 x 7)
   = 700 + 140 + 21
   = 861
3. 12(6 + 7)
   = 12 x 6 + 12 x 7
   = 72 + 84
   = 156

When numbers in brackets are multiplied by a number in front of the brackets, each number inside the brackets is affected. This property of numbers works for addition and subtraction, for example: 4(5 + 6) = (4 x 5) + (4 x 6) or 6(5 – 4) = (6 x 5) - (6 x 4). This property is called the distributive property of multiplication.

Distributive property

What is the answer to 2(4 + 3)?

The "2" outside the brackets is multiplied onto everything that is inside the brackets.

Addition and subtraction are called inverse operations. If you add and subtract the same amount from a number, you end up back where you started. These operations have an effect on each other, for example: 856 + 12 – 12 = 856.
Multiplication and division are called inverse operations. If you multiply and divide a number by the same amount, you end up back where you started as the operations have an inverse effect on each other, for example: 524 x 12 ÷ 12 = 524.