Multiples and Factors - Grade 7 Mathematics Revision Notes

• Factors
  • Prime numbers
  • Multiples
  • Exercise 1 
  • Exercise 2
•  Multiplication and Division
  • Exercise 3
  • Exercise 4
  • HCF and LCM
  • Exercise 5
  • Exercise 6
  • Exercise 7
• BODMAS
  • Exercise 8 

Multiples and Factors

Factors

A factor is a number that divides exactly into a whole number without any remainders. F10 = {1; 2; 5; 10}

Prime numbers

A prime number has only 2 factors: 1 and itself. The number 2 is the first prime number. We say that 2 x 1 = 2. The number 2 is the only even prime number as all other numbers have more than two factors. The numbers 2; 3; 5; 7 and 11 are examples of prime numbers because they have only two factors, the number itself and 1.

e.g. F3 = {1; 3}

3 is therefore a prime number.

Multiples

A multiple is the product of two natural numbers. For example, 24 is multiple of 8 and 3 because 8 x 3 =24. The number 24 is also a multiple of 12 and 2 because 12 x 2 = 24.

Multiplication Tables: M
Multiplication Tables. M7 = {7; 14; 21; 28 ….}

Composite numbers

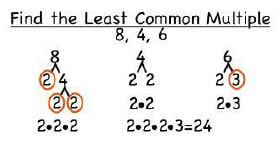
A composite number has more than 2 factors.
e.g. F20 = {1; 2; 4; 5; 10; 20}

Exercise 1 

1. Why is the number 1 neither a prime nor a composite number?
2. Write down the following sets of numbers:
   1. Odd numbers between 100 and 120.
   2. Even numbers from 364 to 372.
   3. Prime numbers greater than 5 but smaller than 27.
   4. Multiples of 8 from 48 to 80.
   5. The factors of 36.
   6. The first 5 counting numbers.
   7. The first 5 natural numbers.
   8. The prime factors of 30.
3. Write down ALL the factors of the following numbers:
   1. 25
   2. 48
4. Write down the first 6 multiples of the following:
   1. 10
   2. 25
5. Solve the problems below by first rounding off each number to the nearest 10 000.
   1. 171 643 + 16 124
   2. 399 106 + 71 257 + 9 199
6. Use the same method again but, round off these numbers to the nearest 100:
   1. 9 876 543 – 210 369
   2. 12 413 x 125
7. Use the same method again but, round off these numbers to the nearest 10:
   1. 8 342 x 29
   2. 211 x 43

Exercise 2

1. What rule is being used in each of these equations: commutative, associative or distributive?
   1. 2(5 – 3) = (2 x 5) - (2 x 3)
   2. 3 + 7 = 7 + 3
   3. 2 x (3 x 4) = (2 x 3) x 4
   4. 5(7 + 6) = (5 x 7) + (5 x 6)
   5. (7 + 9) + 4 = 7 + (9 + 4)
   6. 4 x 7 = 7 x 4

Multiplication and Division

Examples: Multiplication
Calculate 2310 x 35

Answers:
2310 x 35 = 2310 x (30 + 5)
= (231 x 30) + (2310 x 5) Distributive law
= (2310 x 5) + (2310 x 30) Commutative law
= 11550 =69 300
= 80850

In columns, it looks like this:
2310
x 35
11 550               2310 x 5, multiply by units
+ 69 300           2310 x 30, multiply by tens
80 850              Add the two products together

Division
When we divide large numbers, we use a method called long division.

Example:
        453 This number is the answer
321√145413
        1284          321 x 4 = 1284
      1701           Subtract 1284 from 1454 and bring down the 1
      1605           321 x 5 = 1605
      963             Subtract 1605 from 1701 and bring down the 3
      963             321 x 3 = 963
       0                Subtract 963 from 963

Exercise 3

Do these calculations. Show your method. Not just an answer.

1. 432 128 - 248 529
2. 164 600 + 196 416
3. 35 x 78
4. 5 822 ÷ 16
5. 80 357 + 619 450
6. 231 609 – 218 344
7. 27 x 39
8. 9 206 ÷ 28

Exercise 4

1. Use the HORIZONTAL METHOD
   1. 456 +350 + 239
   2. 648 + 352 + 371
2. Use the VERTICAL METHOD
   1. 1 226 x 82
   2. 3 437 x 24

HCF and LCM

The HCF and LCM are numbers that share the same factors. These are called common factors and you can find the highest common factor, HCF, of two or more numbers.
You can also find the lowest common multiple, LCM, of two or more numbers.

Example:
The multiples of 12 are 12 ; 24; 36; 48; 60; 72 ; 84; … and the multiples of 15 are 15; 30; 45; 60; 75; 90; …which means that the LCM of 12 and 15 is 60.
You can use the prime factor method for finding the LCM (or an HCF).

For example:
12 = 2 x 2 x 3 and 15 = 3 x 5 so the LCM is 2 x 2 x 3 x 5 which contains all possible prime factors of both numbers. The HCF of 12 and 15 is 3 as that is the highest factor common to both numbers.

Use prime factors to write numbers in the Factor tree method

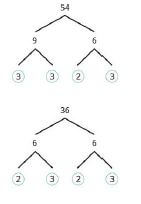
Use prime factors to write numbers in exponential form (Ladder method)

72 = 2 x 2 x 2 x 3 x 3 
= 2³ x 3²

Exercise 5

Write in exponential form using only prime numbers as bases. (Ladder Method)

1. 125
2. 256
3. 200
4. 275
5. 588
6. 576
7. 42
8. 484
9. 1125

Exercise 6

1. Find the HCF of:
   

   a	6 and 9:
   b	14 and 18:
   c	30 and 24:
   d	15 and 10:

2. Find the LCM of:
   

   a	5 and 3:
   b	9 and 6:
   c	8 and 10:
   d	12 and 9:
   e	15 and 20:

Exercise 7

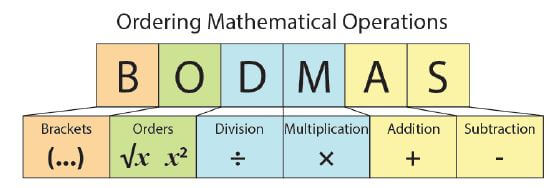
BODMAS stands for Brackets, Of, Division, Multiplication, Addition, and Subtraction.
BODMAS is the order of operation of a mathematical expression.
BODMAS is an acronym to remember the order of mathematical operations – the correct order in which to solve Mathematics problems.

Complete the sums below using BODMAS/BOMDAS.
No CALCULATORS are allowed. Show all working out.

1. 30 X 12 ÷ 4 + ¾ 0f 20
2. (17 x 25) x ( 24 ÷ 2 ) – 10 x 10
3. (24 – 14 ) x 25 ÷ 5
4. 235 + 80 x 50 ÷ 10 – ( 215 + ¾ of 8 )
5. 200 ÷ 20 + 285 ÷ 95 – 8 + 4
6. 790 + 1 000 ÷ 125 – 50 ÷ 10
7. 50 + 35 of 75 – 32
8. 470 + 692 x 10 ÷ 20 – 630

PROBLEM SOLVING: BRAIN TEASER
Two lighthouse beacons can be seen from the top of a hill. These two beacons start flashing at the same time. One beacon flashes every 4 minutes and the other flashes every 9 minutes.
Calculate how long it will be before they both flash at the same time again. Use your 4 x and 9 x table to calculate.

Exercise 8

There are special rules that apply to the number zero and the number one.

1. What happens to numbers when you multiply or divide by 1?
   Solve these problems.
   1. 28×1 =
   2. 28÷1 =
   3. 8 344×1 =
   4. 8 344÷1 =
   5. What can you conclude about multiplying or dividing by 1?
2. What happens to numbers when you add or subtract 0?
   Solve these problems.
   1. 429+0 =
   2. 429−0 =
   3. 5 360+0 =
   4. What can you conclude about adding or subtracting 0.
3. What happens when we multiply by 0?
   1. What does it mean when we say 4×0?
4. What happens when we divide 0 by a whole number?
   1. 0÷4
   2. 0÷8
   3. 0÷58
   4. 0÷347
5. What happens when we divide by zero?
   1. 4÷0
   2. 8÷0
   3. 58÷0
   4. 347÷0