Decimals and Place Value - Grade 7 Mathematics Revision Notes

• Decimal fractions
• Decimals and place value
  • Exercise 21
• Decimal fractions and rounding off
  • Exercise 22
• Comparing and ordering decimals
  • Exercise 23
• Converting to common fractions and percentages denominators of 10, 100 or 1000
  • Exercise 24
• Converting to percentages
  • Exercise 25
• Addition and subtraction of decimals
  • Exercise 26
• Multiplication of decimals- horizontal multiplication
• Vertical multiplication
• Multiplying by 10, 100 and 1000
  • Exercise 27
• Division of decimals. horizontal (short) division
  • Exercise 28

DECIMALS

DECIMAL FRACTIONS
What is a decimal fraction?

• A decimal fraction is a number that is written with a comma.
• Decimals are commonly used to indicate temperature, length, mass, money, and other forms of measurement.
• Proper (common) fractions can be expressed in a decimal form
  e.g. 4,9 = 4 ⁹/₁₀

If we have 9 units and we add 1 more, we now have a Ten.

Each place value on the left is 10 times bigger than the one on the right, e.g.

• 1 x 10 = 10 (T)
• 10 x 10 = 100 (H)
• 10 x 100 = 1 000 (TH)
• 10 x 1 000 = 10 000 (TTH)
• 10 x 10 000 = 100 000 (HTH)
• 10 x 100 000 = 1 000 000 (M)

SO:

• 10 x 0,1 = 1 (U)
• 10 x 0,01 = 0,1 (t)
• 10 x 0,001 = 0,01 (h)
• 10 x 0,0001 = 0,001 (th)

DECIMALS AND PLACE VALUE
The place value table can be represented as follows:
Place value is very important when working with decimals!

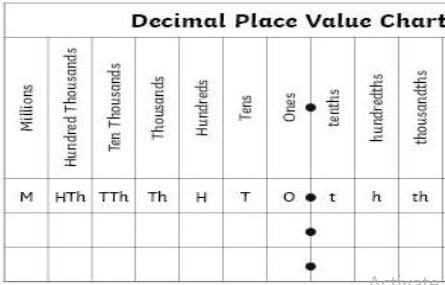
Exercise 21
Use the place value table (if you need to) to complete the following:

1. Give the place value of the underlined digits:
   1. 76 321, 94
   2. 74 856 984, 253
   3. 1 036 942, 375
   4. 362, 125
   5. 965 324, 217
2. Fill in >, < or =:
   1. 45 h________ 0,045
   2. 7,23 _______7,321
   3. 98,24 ______98,204
   4. 712 th_______ 7,12
   5. 146,38 _______146,380

DECIMAL FRACTIONS AND ROUNDING OFF
Remember:

1st decimal place = tenths
2nd decimal place = hundredths
3rd decimal place = thousandths
WHOLE NUMBER = UNIT

The first digit to the right of decimal point is in the tenths place. The second digit to the right of decimal point is in the hundredths place. The third digit to the right of decimal point is in the thousandths place.
When rounding off a decimal, the rules for rounding off stay the same, i.e.

• If the number to the right of the number being rounded off is between 0 and 4, the number being rounded remains the same.
• If the number to the right of the one being rounded off is between 5 and 9, the number being rounded off moves up by 1.
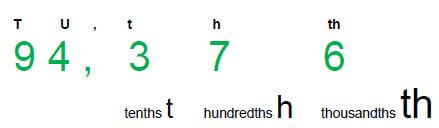
• To read this number correctly we would say: Ninety- four comma three seven six.
• That means we have 9 tens, 4 units, 3 tenths, 7 hundredths and 6 thousandths.

Exercise 22

1. Round off to the nearest whole number:
   1. 0,751
   2. 48,386
   3. 1298,3
   4. 9 999 999,999
   5. 0,6
2. Round off to the second decimal place:
   1. 796 125,324
   2. 908,001
   3. 18,967
   4. 0,008
   5. 0,425

COMPARING AND ORDERING DECIMALS
When you compare decimal fractions, it is much easier to do so if the number of digits to the right of the decimal comma is the same in both decimal fractions.
We can always add 0’s to the right of the decimal fraction without changing its value.
For example, the number 2,367 = 2,36700

Examples:
Arrange the following decimal fractions in ascending order:
3,31; 3,301; 0,301; 3,4; 33,013; 3,41

Answer:
We first need to make sure that all the decimal numbers have the same number of digits to the right of the decimal number. We do this by adding zeros.
3,310; 3,301; 0,301; 3,400; 33,013; 3,410
We then look at the whole numbers and arrange these in ascending order, not worrying about the fractional part yet.
0,301; 2,210; 3,301; 3,400; 3,410; 33,013
Then we arrange the numbers with equal whole number parts in ascending order by looking at the fractional part of the decimal fractions and comparing them.
0,301; 3,301; 3,310; 3,400; 3,410; 33,013

Exercise 23

1. Arrange each of the decimal sequences below in descending order:
   1. 74,302 74,23 74,203 74,3 74,32
   2. 115,7 115,099 115,709 115,9 115,79
2. Arrange each of the decimal sequences in ascending order:
   1. 43,18 43,089 43,0 43,097 43,819
   2. 734,9 734,099 734,090 743,99 734,909
3. Fill in the next 3 numbers to complete each sequence:
   1. 0,3 0,6 0,9
   2. 11,6 11,4 11,2
   3. 3,25 3,5 3,75
   4. 0,85 0,9 0,95
   5. 6,5 6,25 6,0

CONVERTING TO COMMON FRACTIONS AND PERCENTAGES DENOMINATORS OF 10, 100 OR 1000

• When studying common fractions, you discovered that the denominator must be 10, 100 or 1000 before it can be converted to a decimal fraction.
  e.g. 13¹/₂ = 13¹/₂ x ⁵/₅ = 13⁵/₁₀ = 13,5
• When converting from a decimal to a common fraction, first give the fraction a denominator of 10, 100 or 1000 and then simplify the fraction,
  e.g. 28,35 = 28³⁵/₁₀₀ ÷ 55 = 28⁷/₂₀
• Remember: Always give the simplest form!

Exercise 24

1. Convert the decimals below to common fractions in their simplest from:
   1. 25,4
   2. 12,09
   3. 0,975
   4. 1,125
   5. 101,58
   6. 84,499
2. Convert the following fractions to decimals:
   1. 645 1225
   2. 1699 250
   3. 6 1420
   4. 98
   5. 12 18
   6. 35

CONVERTING TO PERCENTAGES

• A percentage is always out of 100
• Percentages are closely linked to common and decimal fractions

If you can, simply change the denominator to 100. What you do to the bottom, also do to the top.
E.g. ¹⁷/₅₀ = *                  3¹/₂₅ = *
¹⁷/₅₀ × ²/₂ = ³⁴/₁₀₀         =⁷⁶/₂₅ × ⁴/₄ = ³⁰⁴/₁₀₀
= 34%                           = 304%
= 0,34                          = 3,04

If the denominator cannot be changed to 100, simply multiply by ¹⁰⁰/₁

E.g. ¹⁹/₃₀= *
= ¹⁹/₃₀ × ¹⁰⁰/₁
= ¹⁹⁰/₃
= 63,3
∴¹⁹/₃₀= ^63,3/₁₀₀=63,3%
= 0,63

Exercise 25

1. Convert to percentages and decimals and show your working out:
   1. ¹/₂
   2. ³/₅
   3. ⁸/₂₅
   4. 1⁷/₂₀
   5. 18⁴/⁵
2. Convert the percentages to decimals and then to common fractions in their simplest form:
   1. 80%
   2. 68%
   3. 91%
   4. 8%
   5. 102%

ADDITION AND SUBTRACTION OF DECIMALS
When adding or subtracting decimals, remember the following:

• All the decimal commas must be in line with one another
• Use zero as a place holder if some numbers have more decimal places or values than others

Example 1:                            Example 2:
142,7 + 6,395 + 12,42         15,8 – 2,345
142,700                               15,800
6,395                                  - 2,345
+12,420                              13,455
161,515

Exercise 26

1. Complete the following:
   1. 27,046 + 1436,2
   2. 8,8 – 3,796
   3. 0,789 + 65,7
   4. 15,81 – 7,9
   5. 41,2 + 2,704 + 715,437
   6. 951,283 – 12,9
   7. 99.875 + 2,1 + 112
   8. 53,6 – 17,154
   9. 0,006 + 1043,9 + 712,38
   10. 71,947 – 3,26

MULTIPLICATION OF DECIMALS- HORIZONTAL MULTIPLICATION
This is a mental process that can be carried out without showing the method.
This should be used for basic probems only.

Example:
6 x 0,02 → Ask what 6 x 2 is. Write the answer of 12, then count
= 12           how many spaces there are after the comma.
= 0,12        Insert the comma in the answer

Other examples:
0,7 x 0,3 = 0,21         1,5 x 0,3             = 0,45
0,08 x 0,2 = 0,016     0,004 x 0,003     = 0,000012

Can you see how we arrived at these answers? Discuss this is class.

VERTICAL MULTIPLICATION

• Follow the same method you would use to multiply whole numbers.
• Ignore the decimal comma in your method.
• Once you have worked out the answer, check how many decimal places were after each number. Count the spaces, in the answer (from the right) and insert the comma.
• You need not line up the commas underneath each other.

Example 1:                                 Example 2:
483,2 x 7                                    13,5 x 2,4
483,2 (1 place after the              13,5 (1 place after the comma
x 7 comma)                                 x2,4 comma + 1 place comma)
3382,4 (1 place after the comma) 540 (leave out the comma) 

                                       +2700
                                                   32,40 insert comma after 2 numbers.

MULTIPLYING BY 10, 100 AND 1000

Study the examples below:
0,6 x 10 = 6                     0,23 x 1000 = 230
0,145 x 100 = 14,5          0,002 x 104 = 20

You should see that when you multiply by 10, 100 or 1000 to make the number bigger, the number of times the comma “moves” is in direct relation to the number of zeroes there are in the number you are multiplying by:

i.e.

• x 10 moves one space to the right
• x 100 moves two spaces to the right
• x 1000 moves three spaces to the right

Exercise 27

1. Complete the following:
   1. 0,4 x 0,09
   2. 4,3 x 0,007
   3. 6,2 x 0,05
   4. 32,6 x 0,8
   5. 8,7 x 2,4
2. Complete the following:
   1. 23,7 x 2,5
   2. 56,72 x 6,4
   3. 6,7 x 8,6
   4. 589,6 x 0,8
   5. 432,54 x 1,7
3. Write down the answers to the following:
   1. 14,06 x 1000
   2. (0,2)²
   3. 0,007 x 10
   4. 4,59 x 10³
   5. 125,3 x 100
4. Complete the following:
   1. 71,83 x 6000 
   2. 9,836 x 4000
   3. 0,007 x 10
   4. 98,6 x 500
   5. 412,6 x 90
5. Select the best and easiest method to solve each of the following:
   1. A tour to certain parts of South Africa costs R4698,35 per person. If 68 tourists go on the trip, how much money will be collected?
   2. A local deli sells cheese for R29,99 per kilogram. What will it cost me if I buy 3½ kg of cheese?
   3. Liane earns R54,75 for every 1 hour shift she works. If she works 8 hours a day over 100 days, what will her total earnings be?
   4. A greengrocer sells peaches for R3,99 per kilogram. A customer selects some peaches and is told that her fruit weighs 5,2 kg. How much money must she pay the greengrocer?
   5. A money-lending business charges R68,75 interest per day on a loan that it made to a client. How much interest does the client have to pay for the month of April?

DIVISION OF DECIMALS. HORIZONTAL (SHORT) DIVISION
This mental process can be carried out without showing the method.

This should be used for basic problems only.

Example:
85,635 ÷ 9 = 9,515

Dividing by 10, 100 OR 1000
Study the examples below:
21,795 ÷ 10 = 2,1795

469,837 ÷ 1000 = 0,469837

3,46 ÷ 100 = 0,0346

78 346,27 ÷ 104 = 7,834627

You will notice that when dividing by 10, 100 or 1000 to make the number smaller, the number of times the comma “moves” is linked to the number of zeroes in the number you are diving by.

• ÷ 10 : comma moves 1 space to the left
• ÷ 100 : comma moves 2 spaces to the left
• ÷ 1000 : comma moves 3 spaces to the left

Dividing by multiples of 10, 100 OR 1000
When you multiplied by numbers of 10, 100 or 1000, you did the following:

71,246 x 30
= 71,246 x 10 x 3
= 712,46 x 3
= 2137,38

When you divide by multiples of 10, 100 or 1000, you follow the same procedure. However, this time you need to replace the X signs with ÷ signs because you are doing a division sum.

Example:
493,64 ÷ 700
= 496,64 ÷ 100 ÷ 7
= 4,9664 ÷ 7
= 0,705

Exercise 28

1. Complete the following:
   1. 71,435 ÷ 7
   2. 24,1 ÷ 4
   3. 6,257 ÷ 5
   4. 288,144 ÷ 12
   5. 837,84 ÷ 6
2. Write down the answers to the following:
   1. 165,2÷ 1000
   2. 143 725,811 ÷ 1000
   3. 18,976 ÷ 10
   4. 0,8 ÷ 100
   5. 0,0731 ÷ 100
3. Use any method to complete the following:
   1. 29,185 ÷ 50
   2. 571,424 ÷ 700
   3. 32,13÷ 9000
   4. 146,5÷ 20
   5. 8166,128 ÷ 400