Fractions - Grade 7 Mathematics Revision Notes

• Proper and improper fractions
• Mixed numbers
• Converting fractions
  • Exercise 12
• Simplifying fractions
  • Exercise 13
• Fractions of quantities
  • Exercise 14
• Giving parts of quantities as fractions
  • Exercise 15
  • Exercise 16
• Addition and subtraction of common fractions
  • Exercise 17
• Multiplication of fractions
  • Exercise 18
  • Exercise 19
  • Exercise 20

FRACTIONS

PROPER AND IMPROPER FRACTIONS
A fraction is a portion of a whole that has been divided into equal parts.

A common fraction is written as ½ or ¼ or ¾.

The number at the top represents a whole number called the numerator and the number at the bottom represents a whole number called the denominator.

In proper fractions, the numerator of the fraction is smaller than the denominator.
In improper fractions, the numerator of the fraction is bigger than the denominator.

MIXED NUMBERS
Sometimes we write an improper fraction as a mixed number, for example:

We would write ⁸/₅ as 1 ³/₅
The mixed number has a whole number part and a fraction part.

CONVERTING FRACTIONS
To convert an improper fraction to a mixed number, simply divide the number by the denominator:

Example:

¹²/₅ = 12 ÷ 5 = 2 r 2

We write this as 2 ²/₅

To convert a mixed number to an improper fraction, multiply the whole number by the denominator. Add the numerator to this. Write this answer as the numerator and keep the denominator the same.

Examples:
8 ½ = Multiply 8 by 2, and then add 1
This will give you a total of 17
The improper fraction will therefore be ¹⁷/₂

Exercise 12

1. Convert the improper fractions to mixed numbers:
   ⁴¹/₉ ³¹⁶/₃ ¹⁹⁹/₁₀ ⁴¹²/₁₅ ¹⁰⁰⁰/₁₂₅
2. Convert the mixed numbers to improper fractions:
   13²/₃; 17⁸/₁₁; 4³/₇; 6⁴/₁₅; 9⁷/₁₂

Equivalent fractions

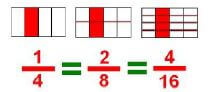
SIMPLIFYING FRACTIONS
To simplify a fraction, you must reduce the fraction to its smallest form.
To do this, you need to divide both the numerator and the denominator by the same highest common factor.

Example:¹²/₃₀ = ∗
The highest number that can fit into both 12 and 30 is 6.
6 is therefore the highest common factor (HCF)
Divide the numerator and denominator by the highest common factor.

e.g. ¹²/₃₀÷ ⁶/₆ = ²/₅
SO: ¹²/₃₀= ²/₅

NB: A common fraction must always be written in the simplest form!

Exercise 13

1. Equivalent fractions
   1. ³⁰/₃₅ = ^∗/₇
   2. ¹¹/₄₄ = ¹/∗
   3. ⁶³/₉₀ = ⁷/_∗
   4. ⁹/₁₁ = ⁹⁹/_∗
2. Simplifying fractions
   1890 ; 3²⁵/₄₅ ; 9⁴⁶/₁₁₂ ; 5²⁴/₆₀

FRACTIONS OF QUANTITIES
When asked to work out a fraction of a quantity, use one of the following methods:

Method 1:
¹/₁₀ of 30 (Bodmas Rule: “of “ becomes x)
= ¹/₁₀ × ³⁰/₁ (Multiply numerators, then denominators)
= ³⁰/₁₀(÷ ¹⁰/₁₀) (Reduce answer to simplest form)
= ³/₁ = 3

Method 2:
¹/₁₀ of 30 (÷by 10; x1)
= 3

Exercise 14

1. ³/₄ of 200
2. ⁷/₁₀ of 150
3. ⁵/₈ of 800
4. ⁴/₅ of 375

GIVING PARTS OF QUANTITIES AS FRACTIONS
First change the amounts to the same unit of measurement.
Write both amounts as fractions.
Reduce the fraction to its simplest form.

Example: What fraction is 20c of R2?
R2 = 200c (Same unit of measurement)
= ²⁰/₂₀₀ ÷ ²⁰/₁₀ (Both amounts as fractions)
= ¹/₁₀ (Simplest form)

Exercise 15

1. Solve the problems given below, in your books, and remember to show your workings:
   1. What is ³/₄ of 640?
   2. What is ²/₃ of 900?
   3. What fraction is ⁵/₈ of 800?
   4. What is ⁵/₆ of 300?
   5. What fraction is 14 hours of 1 week?

Exercise 16

1. Complete by filling in >, < or =. Show your working out:
   1. ⁹/₁₀ ............. ¹⁹/₂₀
   2. ⁸/₉ .............⁹/₁₀
   3. ¹⁸/₄₀ ............. ⁵⁰/₆₀
   4. ⁸/₁₂ ............. ¹²/₁₈
   5. ⁵/₇ ............. ⁷/₈
   6. ¹⁷/₃₄ .............  ⁵¹/₁₀₂
2. Arrange these fractions in descending order, show your working out:
   1. ⁵/₁₂ ³/₄ ¹/₃ ⁵/₆ ⁷/₉
   2. ¹/₄ ¹/₂ ¹¹/₂₄ ⁵/₆ ⁸/₁₂
3. Arrange these fractions in ascending order, show your working out:
   1. ²/₃ ⁶/₇ ¹/₂ ¹⁵/₂₁ ⁸/₁₄
   2. ³/₄ ²/₃ ⁵/₆ ⁸/₉ ¹¹/₁₂

ADDITION AND SUBTRACTION OF COMMON FRACTIONS
If the denominators are different, you must make them the same by finding the lowest common denominator.
Remember that when changing to the LCD, what you do to the bottom must be done to the top!
Also remember that you must always write your answer in the simplest form.

Exercise 17

1. 1 ⁷/₈ + 4 ²/₅
2. 11 ³/₇ - 7 ³/₄
3. 2 ¹/₂ + 1 ¹/₉
4. 8³/₁₈ + 1 ⁷/₃₆ + 4 ¹/₂
5. 3 ⁴/₅ + 7 ³/₁₀ - 1 ¹/₂
6. 6 ²/₉ - 1 ¹/₃
7. 10 ²/₃ + 5 ¹/₂− 4 ¹/₄
8. 4 ³/₅ - 2 ³/₄ + 10 ²/₃
9. 2 ⁵/₆ + 1 ²/₃ -2 ⁴/₈ - 1¹/₆

MULTIPLICATION OF FRACTIONS
If you are asked to multiply mixed numbers, first change these to improper fractions. Continue with the same method as before, ensuring that the answer is simplified.

Example:
³/₅ × ⁴/₁
= ²⁸/₅ × ¹⁷/₄
= ¹¹⁹/₂₀
= 23 ⁴/₅

Exercise 18
Complete the following:

1. 1 ³/₁₀ × 2 ¹/₂
2. 3 ⁴/₅ × 2 ⁵/₁₀
3. ²/₉ × 15 ¹²/₁₅
4. 3 ³/₈ × 6 ¹/₂ × 2 ²/₃

Exercise 19
Mixed Exercise:

1. 1 ³/₅ + 2¹/₃ + 3⁴/₁₅
2. 10⁴/₇ − 3¹/₃
3. 4 ⁵/₆ × 3⁹/₁₀
4. 2³/₄ + 3⁷/₈ −1³/₅ × 2⁵/₆
5. 5³/₇ × 3¹/₃ − 2¹/₂
6. 6²/₄ + ²/₈ of 3 + 2³/₆

Exercise 20

1. A baker uses 1 ⁴/₅ of a 10kg bag of flour each day.
   How much flour does he use?
   1. In a day
   2. In a week
2. A recipe for biscuits makes 24 biscuits. A baker needs to make 3 ³/₄ of that amount. How many biscuits will he make?
3. Kimera is given R240. Her mother tells her to spend ³/₈ on flour, ¹/₅ on sugar and to bring home the change.
   1. What fraction of the money will she bring home?
   2. How much money will this be?
4. Oliver’s petrol tank is ⁴/₅ full. His car will use ¹²/₁₅ of this amount to complete its next journey.
   What fraction of petrol will be used?
5. A shop keeper grants a discount of ²/₃ off a damaged product so that he can clear a space for his new stock. The original sale price is R330. How much will the customer pay for the damaged product?
6. Siya is given R450 for his birthday. He uses ¹/₅ to buy shoes, ¹/₁₅ on CDs, ¹/₆ for games and ¹/₂ on clothes.
   1. What fraction of the money has been spent?
   2. How much change will he receive?
7. There are 185 learners in a Grade Seven group. ³/₅ of these learners are girls. How many boys are there?