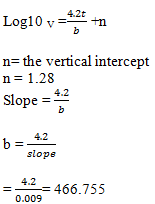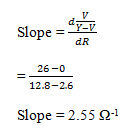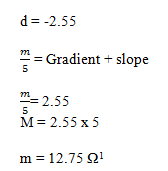QUESTION 1
You are provided with the following apparatus
- Two beakers.
- A complete retold stand.
- Funnel
- Cotton wool.
- Access to water.
- Stop watch.
- A burette with a tap (50cm3).
- 100ml measuring cylinder.
Proceed as follows:
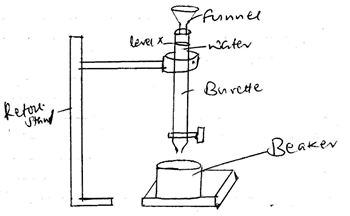
- Set the apparatus as follows:
- Support the burrete on a result as shown above
- Close the tap of the burrete and fill it with water to the brim
- Transfer the water to the 100ml measuring cylinder and record the volume of the water
Volume V1 = 65cm3 (1mk)
- Fill the burrette with water up to the 0cm3 mark. Drain this water into 100ml measuring cylinder and record its volume V2
V2= 53 cm3 (1mk)
The excess water above the zero mark is given by
V0 = V1 – V2
V0 = 65 − 53 = 12 cm3 (1mk)
(This volume should be added to the final volume of the burette reading when water has been drained) - Fill the burrete with water to the brim. Finally open the tap at once and start the stop watch simultaneously. Obtain the time, t taken for the level of water to reach X=10cm3
Volume drained = (V0+10) cm3
Refill the burette with water. Finally open the tap at once and start the stopwatch simultaneously. Obtain the time taken for the level of water to reach x = 20cm3
Volume drained = (V0+20) cm3 - Repeat the procedure for other values of the burette readings.
Record the volume drained and the corresponding time in the table below.
(9marks)Burette Reading X (cm3) Volume of water drained
v = (Vo + x)cm3Time t(s) Log10V 10 22 15.90 1.3424 20 32 23.29 1.5051 30 42 33.15 1.6232 40 52 44.12 1.7160 45 57 49.50 1.7559 50 62 59.28 1.7924 - Plot the graph of log10v (vertical axis) against time t. (5mks)
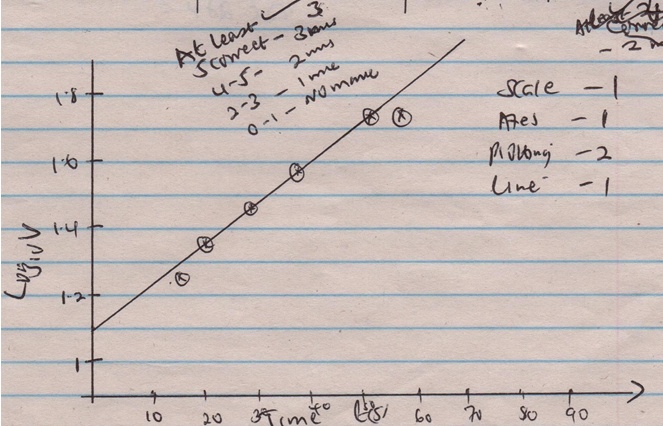
Slope = (1.88 − 1.3)/(64 − 0)
= 0.58/64 = 0.009 s-1 - Using your graph, calculate the value for b and n from the equation. (3mark)
Log10 V = 4.2t/b + n
- Plot the graph of log10v (vertical axis) against time t. (5mks)
QUESTION 2
- You are provided with the following apparatus:
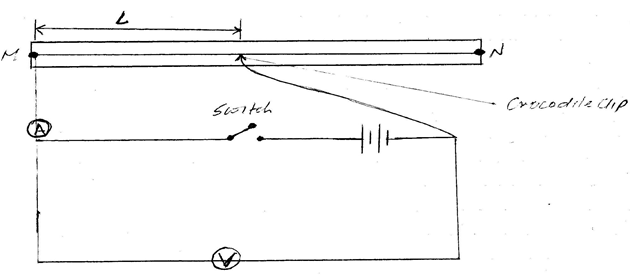
- Resistance wire fitted on a scale labelled MN
- Switch
- Voltmeter (0.3v) or(0.5v)
- Ammeter (0.1A)
- Two dry cells
- Six connecting wires
- Remove the crocodile clip from the resistance wire MN and close the switch. Record the voltmeter reading.
Y= 2.7 V (1mk) - Attach the crocodile clip to the resistance wire such that L=10cm.
- Record the voltmeter and ammeter reading in the table below.
- Repeat the procedure in (iii) and (iv) for L= 20 cm, 30 cm, 40 cm, 50cm, 60 cm, 70cm and 80 cm.
- Complete the table below. (9mks)
Length L (cm) 10 20 30 50 80 Current I (A) 0.86 0.48 0.43 0.255 0.205 P.d. V (V) 2.1 2.3 2.4 2.5 2.6 y − v 0.6 0.4 0.3 0.2 0.1 V/Y−V 3.5 5.75 8.0 12.5 26 V/I = R (Ω) 2.44219 4.717 5.5814 9.8039 12.6829 - At least 3 correct readings row 1 and 2 - (2mks)
- 4-5 correct reading row 1 & 2 – (3 mks)
- Row 3 & 4 all correct - (1mk)
- Plot the graph of V/Y−V, vertical axis against R (5 marks)
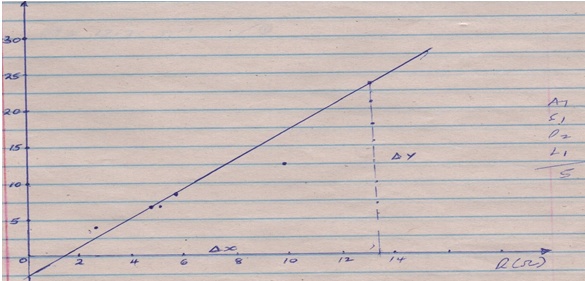
- Determine the slope, m of the graph (2mks)
- The graph is given by the equation
V/Y−V = MR/5 + d
Determine the value of m and d (3 marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download PHYSICS PAPER 3 Marking Scheme - 2019 KCSE Prediction Answers Set 2.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students