Question 1
You are provided with the following apparatus
- Micrometer screw gauge
- A plastic drinking straw
- A white label with a horizontal line across the centre
- Some plasticine mass 5.0 g
- Half a meter rule
- A 200 ml beaker
- A 100 ml measuring cylinder
- Two rubber bands
- Seven shoe tacks
- Electronic beam balance
- Jockey
Proceed as follows- Place the seven shoe tacks on the eletronic beam balance and record the mass M. 1.7g
M=(1.5 to 2.0) × 10-3kg or 0.0017 kg or 0.002kg (3 d.p or 4 d.p) (1mk) - Given that W = 1.429 M, where W is the weight of one tack, determine the value of W
W= 1.429 × 0.0017 (½ mk) = 0.0024293 N(½mk)
(0.0021435 to 0.002858) -
- Fix the half meter rule vertically agaisnt the measuring cyliner using rubber band with the zero mark of the half meter rule at the bottom of the measuring cylinder
- Measure 150ml of water using the beaker and pour it into the measuring cylinder.
- Roll the plasticine into a spherical ball and push one ened of the straw into the plasticine to block one end
- Insert the drinking straw with the plasticine into the mesuring cylinder such that it floast vertically
- Remove the straw and fix the white label at 4 cm above the plasticine so that the line at the centre runs horizontally. Ensure the line is submerged under the water as shown below
Record the position of the horizontal line as indicated on the half meter rule
Lo = 17.2 cm (16.5 — 17.5) cm (1mk) - Also record this value in the table as L when there is no shoe tack in the straw.
Insert one shoe tack into the straw and record the new level L of the horizontal line in the table. Repeat the procedure for each number of shoe tacks indicated while recording the level each time.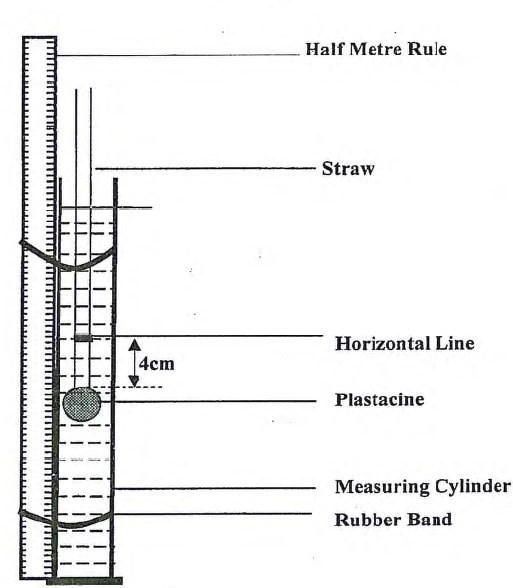
Complete the values of L with number of stacks on the table below (6 marks)
No of shoe tacks N 0 1 2 3 4 5 6 7 Level L (cm) 17.2 16.3 15.4 14.5 13.5 12.6 11.8 11.0 (± 1 cm) h = Lo - L (m) × 10-2 0.0 0.9 1.8 2.7 3.7 4.6 5.4 6.2
No of shoe tacks N 0 1 2 3 4 5 6 7 Level L (cm) 13.0 12.0 11.1 10.3 9.4 8.5 7.6 6.5 (± 1 cm) h = Lo - L (m) × 10-2 0.0 0.9 1.8 2.6 3.5 4.4 5.3 6.4
- On the grid provided plot a graph of h against N (4 marks)
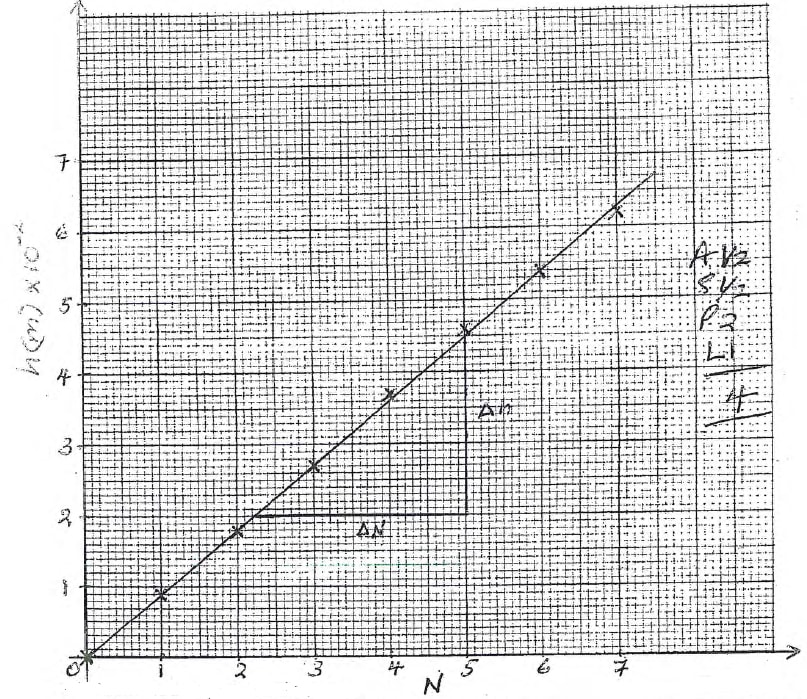
- Determine the slope S of the graph
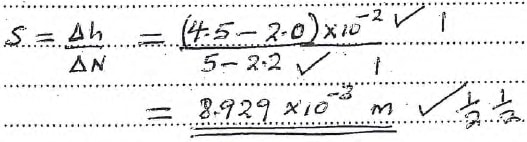
- Given the upthrust U of one shoe tack is given as U = 4πS/10000, determine the value of U (2 marks)
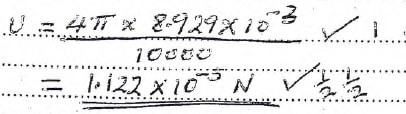
- Determine the apparent weight of one shoe tack (2 marks)
WL= Wa − U
= 0.0024293 − 0.00001122 (1mk)
=0.002418 N (½mk ½mk)
- Place the seven shoe tacks on the eletronic beam balance and record the mass M. 1.7g
Question 2
You are provided with the follwoing
- A carbon resisitor marked X
- Resistance wire marked R
- Micrometer screw gauge (to be shared)
- Voltmeter
- Ammeter
- Resistance wire mounted on a wire labelled L
- A cell, Cell holder
- Centre-zero Galvanometer
- 8 connecting wires
- jockey
- Using the micrometer screw gauge, measure and record the diameter D of the resistance wire R provided
0.40—0.50mm
D= 0.00040 — 0.00050 m (1 mk)
0.00043 m - Set up the following circuit
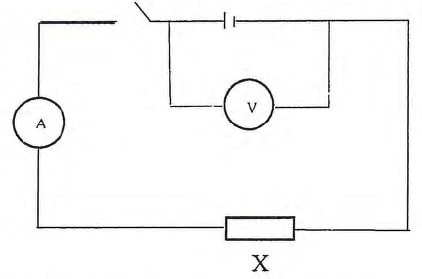
- Record the voltmeter reading when the switch is open
E= 1.65 (1.5—1.7) V Accept 1 dp and 2 dp (1 mk) - Close the switch and record the voltmeter and ameter readings V and I
V= 1.5 (1.4 — 1.6)V (1 mk)
I= 0.12 (0.10—0.14)A (1 mk) - Now connect the voltmeter across the carbon resistor X and record voltmeter reading V1
V1 = 1.4 ± 0.2 V (1 mark) - Compare the values of V and V1 giving a reason why they are different (2 marks)
V1<V or V>V1
There is voltage drop across ammeter and connecting wires - Calculate X1 given that X1 = V1/I
X1= 1.4/0.12 (½ mk)
= 11.67 Ω (½ mk (+ unit) (10—16Ω)
Min X1 = 1.4/0.14 = 10Ω
Max X1=1.6/0.10=16Ω - Calculate the internal resistance r of the cell given that r = (E−V)/I (2 marks)
r = (1.65 − 1.5)/0.12 (1 mk)
=1.252 Ω (½ mk ½ mk) - Calculate X2, given that E = I(X2+r)
X2= E/I − r = 1.65/0.12 − 1.25 (½mk)
=12.5 Ω (½mk) (ignore missing unit) - Calculate X the average values of X2 and X1
X2 = (X1+X2)/2 = (11.67 + 12.5)/2 (½mk) = 12.085 Ω (½mk) Ignore missing unit
- Record the voltmeter reading when the switch is open
- Connect anothe circuit as shown below
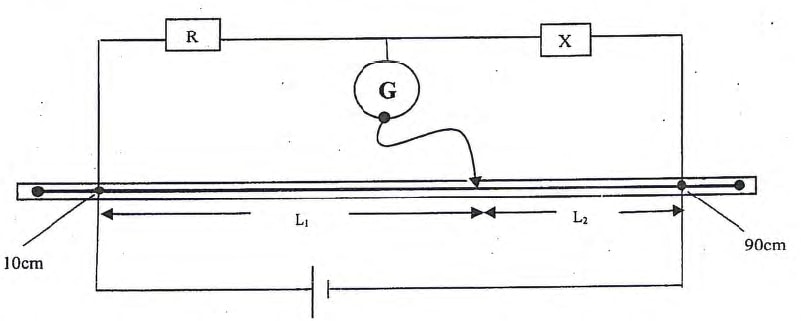
- Move the sliding pointer along the resistance wire until the galvanometer reading comes to zero. Record L1 and L2
L1=21.2 cm (½mk ½mk) L2 = 58.8 cm(½mk ½mk) (L1+L2 = 80) - Obtain the value of the unknown resistance R given that R/X = L1/L2
R= L1/L2 X = (21.2 × 12.085)/58.8 (½mk)
=4.357 Ω (½mk) (ignore missing unit) (5 ± 1 Ω)
L1=57.9 cm (½mk ½mk) L2 = 22.1 cm(½mk ½mk)
X/R = L1/L2
R= L2/L1 X = (12.085× 22.1)/57.9 (½mk)
=4.613 Ω (½mk) - Move the sliding pointer along the resistance wire until the galvanometer reading comes to zero. Record L1 and L2
-
- Calculate the average values of R (1 mark)
R= 4.357 + 4.613/2 (½mk)
= 4.485 Ω (½mk) (ignore missing unit) (5 ± 1 Ω ) - Given that, R= 35S/100πD2 (2 marks)
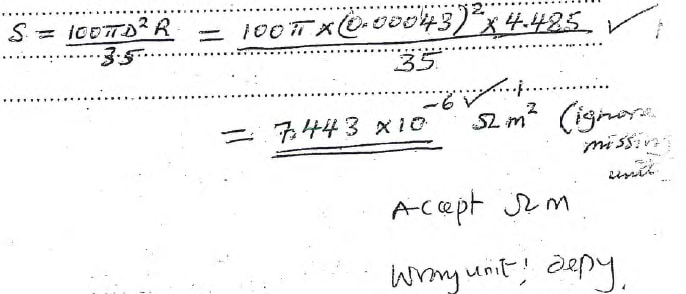
- Calculate the average values of R (1 mark)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download PHYSICS PAPER 3 Marking Scheme - 2019 KCSE Prediction Answers Set 1.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

