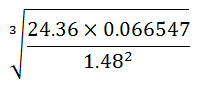SECTION I (50 MARKS)
Answer all the questions from this section
- Use Logarithms correct to four significant figures to evaluate. (4marks)
- Find the percentage error in the total length of four rods measuring 12.5cm, 24.5cm, 12.9cm and 10.1cm all the nearest 0.1cm. (3 marks)
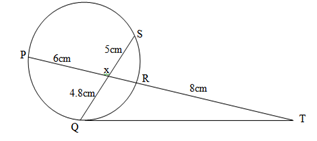
- In the figure below QT is a tangent to the circle at Q. PXRT and QXS are straight lines. PX = 6cm, RT = 8cm, QX = 4.8cm and XS = 5cm.
Find the length of QT (3 marks) - Use the trapezium rule with seven ordinates to find the area bounded by the curve y=x2+1 lines x = −2, x = 4 and x – axis (3 marks)
- Given that
make p the subject of the formula (3 marks)
- Solve for x in the equation below:
Log 3(x + 3) = 3 log 3 + 2 (3 marks) - The points (5, 5) and (−3, −1) are ends of a diameter of a circle centre A. Determine:
- The coordinates of A. (1 mark)
- The equation of a circle expressing it in form x2 + y2 + ax + by + c = 0 (2 marks)
- A transformation is represented by the matrix
. This transformation maps a triangle ABC of the area 12.5cm2 onto another triangle A′B′C′. Find the area of triangle A′B′C′. (3marks)
- Two taps A and B can fill a water bath in 8 minutes and 10 minutes respectively. Tap A is opened for 2 minutes then closed. Tap B is later opened for one minute then closed. How long will the two taps take running together to fill the remaining part of the water bath? (3 marks)
-
- Expand and simplify (1−3x)5 up to the term in x3 (2 marks)
- Hence use your expansion to estimate (0.97)5 correct to 4d.p. (2 marks)
- Solve for x in the equation: for 2cos4x = −1 00 < x < 1800 (3 marks)
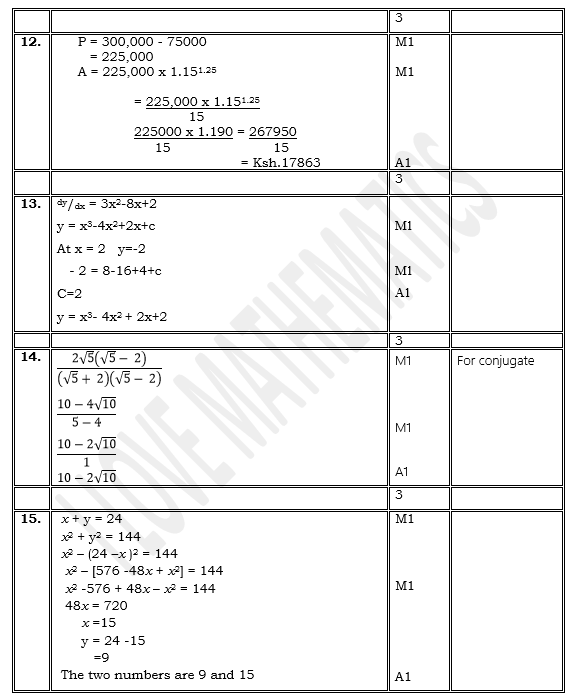
- Wanjiku pays for a car on hire purchase in 15 monthly instalments. The cash price of the car is Ksh.300, 000 and the interest rate is 15%p.a. A deposit of Ksh.75, 000 is made. Calculate her monthly repayments. (3 marks)
- The gradient function of a curve is given dy/dx = 3x2 – 8x + 2. If the curve passes through the point, (2, –2), find its equation. (3 marks)
- Rationalize the denominator and simplify (3 marks)
- The sum of two numbers is 24. The difference of their squares is 144. What are the two numbers? (3marks)
- The data below represents the marks scored by 15 form 4 students in an exam:
58, 61, 40, 37, 39, 40, 41, 43, 44, 37, 70, 44, 47, 36 and 52
Calculate the interquartile range of the above data (3 marks)
SECTION II (50 MARKS)
Answer five questions only from this section
- The following table shows the rate at which income tax was charged during a certain year.
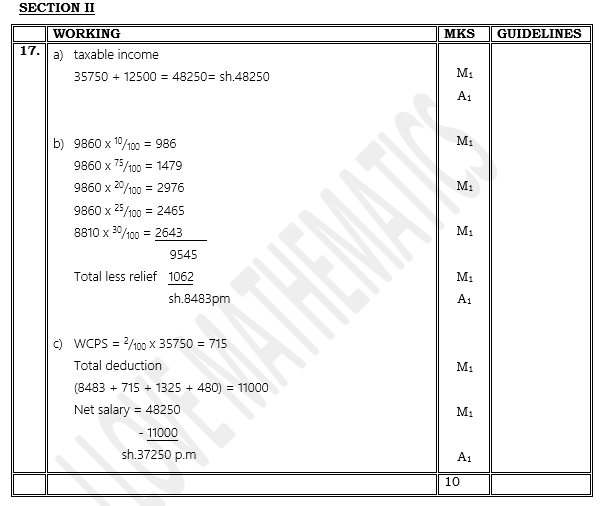
A civil servant earns a basic salary of Ksh.35750 and a monthly house allowance of sh. 12500. The civil servant is entitled to a personal relief of sh. 1062 per month. Calculate:Monthly taxable income in Ksh.
Tax rate %
0 - 9860
10
9861 - 19720
15
19721 - 29580
20
29581 - 39440
25
39441 - 49300
30
49301 - 59160
35
over 59160
40
- Taxable income (2 marks)
- Calculate his net monthly tax (5 marks)
- Apart from the salary the following deduction are also made from his monthly income.
WCPS at 2% of the basic salary
Loan repayment Ksh.1325
NHIF sh.480
Calculate his net monthly earning. (3 marks)
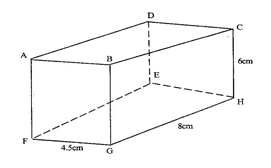
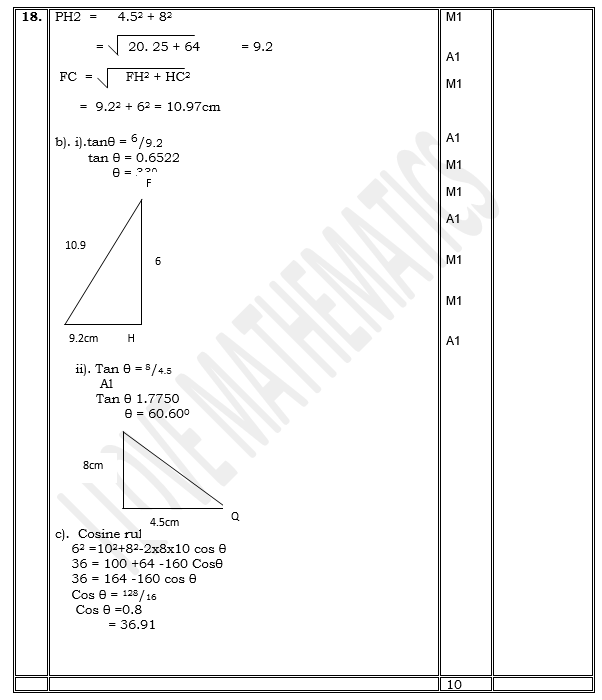
- The diagram below represents a cuboid ABCDEFGH in which FG= 4.5 cm, GH=8cm and HC=6 cm
Calculate:- The length of FC (2 marks)
-
- The size of the angle between the lines FC and FH (2 marks)
- The size of the angle between the lines AB and FH (3 marks)
- The size of the angle between the planes ABHE and the plane FGHE (3 marks)
- A plane S flies from a point P (400N, 450W) to a point Q (350N, 450W) and then to another point T (350N, 1350E). Given that the radius of the earth is 6370 km find the distance from P to Q in Km.(Take π =22/7 ) (2 marks)
- Find in nm
- The shortest distance between Q and T. (2 marks)
- The longest distance between Q and T (to the nearest tens) (2 marks)
- Find the difference in time taken when S flies along the shortest and longest routes if its speed is 420 knots (4 marks)
- Find in nm
- The probability that a pupil goes to school by a boda-boda is 2/3 and by a matatu is 1/4 . If he uses a boda-boda the probability that he is late is 2/5 and if he uses matatu the probability of being late is 3/10. If he uses other means of transport the probability of being late is 3/20.
- Draw a tree diagram to represent this information. (3marks)
- Find the probability that he will be late for school. (3marks)
- Find the probability that he will be late for school if he does not use a matatu. (2marks)
- What is the probability that he will not be late to school? (2marks)
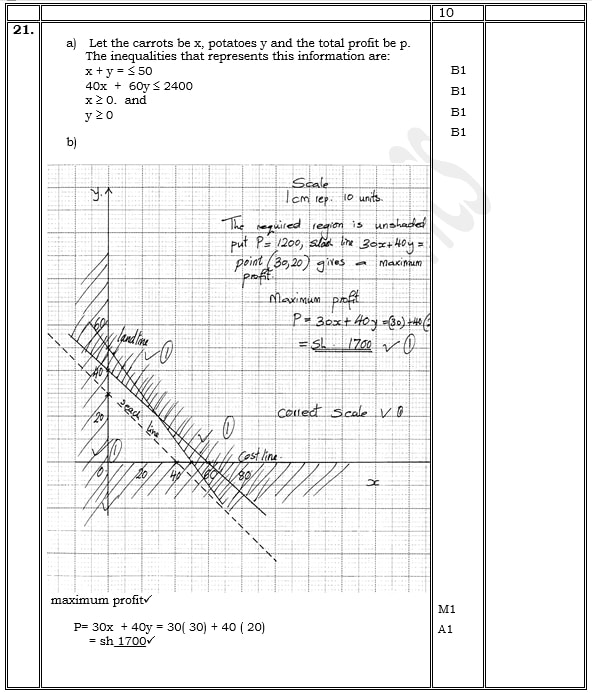
- A farmer has 50 acres of land. He has a capital Shs. 2,400 to grow carrots and potatoes as cash crops. The cost of growing carrots is Shs.40 per acre and that of growing potatoes is Shs. 60 per acre. He estimates that the respective profits per acre are Shs. 30 (on carrots) and Shs. 40 (on potatoes). By letting x and y to represent carrots and potatoes respectively:-
- Form suitable inequalities to represent this information. (4marks)
- By representing this information on a graph, determine on how many acres he should grow each crop for maximum profit. (4marks)
- Find the maximum profit. (2 marks)
- An arithmetic progession is such that the first term is –5, the last term is 135 and the sum of the progression is 975.
- Calculate
- The number of terms in the series (4 marks)
- The common difference of the progression (2 marks)
- The sum of the first three terms of a geometric progression is 27 and first term is 36.
Determine the common ration and the value of the fourth term (4 marks)
- Calculate
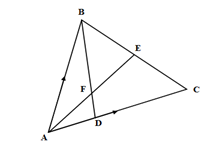
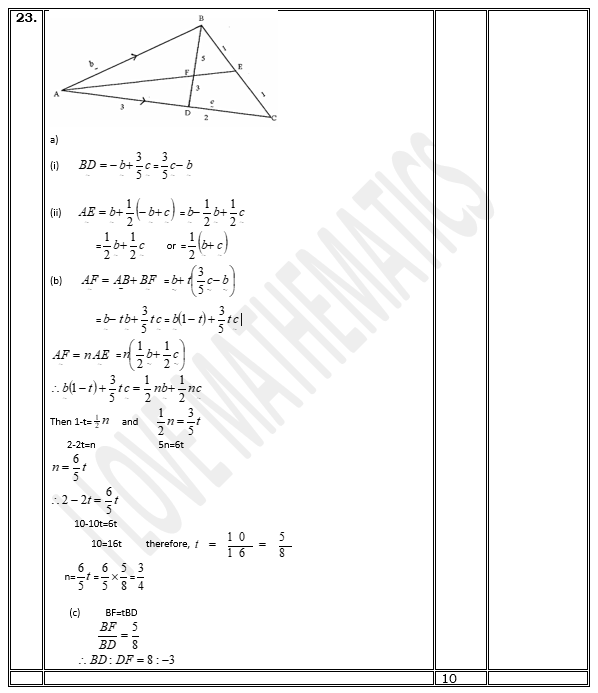
- In the figure below E is the midpoint of BC. AD:DC 3:2 and F is the meeting point of BD and AE.
- If AB = b and AC = c, find:
- BD (2marks)
- AE (2marks)
- If BF = tBD and AF = nAE. Find the value of t and n. (5marks)
- State the ratio of BD to BF. (1mark)
- If AB = b and AC = c, find:
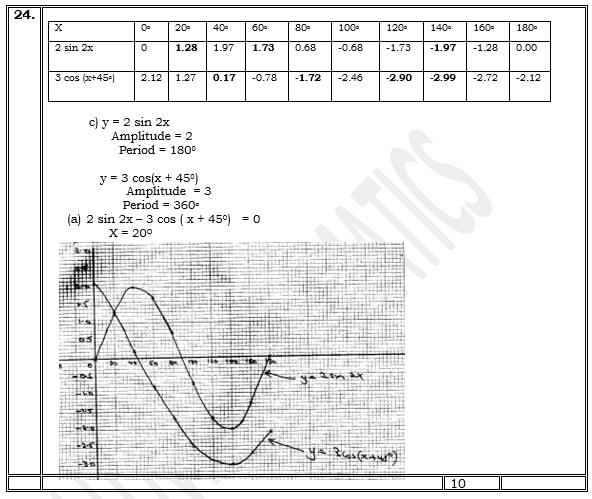
- Given that y = 2sin 2x and y = 3cos (x + 45o)
- Complete the table below. (2mks)
x
00
200
400
600
800
1000
1200
1400
1600
1800
2sin x
0
1.97
0.68
−0.68
−1.73
−1.28
0.00
3cos(x+450)
2.12
1.27
−0.78
−2.46
−2.72
−2.12
- Use the data to draw the graphs of y = 2 sin 2x and y = 3 cos (x + 45o) for 0o ≤x ≤ 180o on the same axes. (4marks)
- State the amplitude and period of each curve. (2marks)
- Use the graph to solve the equation 2 sin 2x – 3cos (x + 450) = 0 for 00≤ x ≤1800 ( 2marks)
- Complete the table below. (2mks)


MARKING SCHEME
Download MATHEMATICS PAPER 2 - 2020 KCSE PREDICTION SET 1 (QUESTIONS AND ANSWERS).
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students