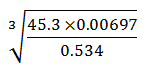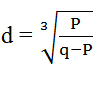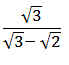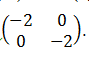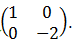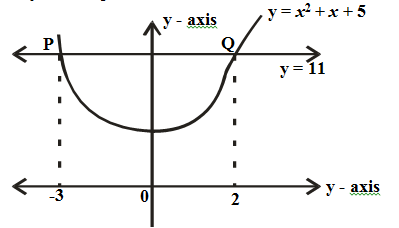MATHEMATICS PAPER 2 - 2017 KITUI MOCK EXAMINATION

SECTION I (50 MARKS)

Answer ALL the questions from this section.

1. Use logarithms to evaluate, (4 marks)
   

2. Make P the subject of the formula (3 marks)
   

3. Find the circle centre and radius whose equation is
   3x² + 3y² + 18x – 6y + 18 = 0                                                                                                      (3 marks)

4. The volumes of two similar cylindrical containers are 27cm³ and 64cm³ Given that the height of the smaller container is 12cm, find the height of the larger container. (2 marks)
5. 3cm³ of water is added to 2cm³ of a certain medicine which costs sh.12 per cm³. The chemist sells the diluted medicine at sh.6 per cm³. Calculate the percentage profit.
   (3 marks)
6. Given that 4y = 3 sin ²/₅ for 0 < θ< 360^o. Determine
   1. The amplitude of the curve (1 mark)
   2. The period of the curve. (1 mark)

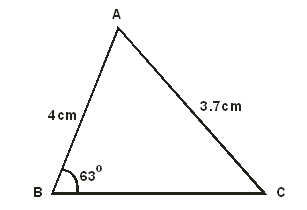
7. Find the length BC of the following triangle if AC = 3.7cm, AB = 4cm and angle ABC = 63^o. (3 marks)
     

8. Solve for x in the equation
   27^{x - 1} 3^{x + 1} = 729                                            (3 marks)

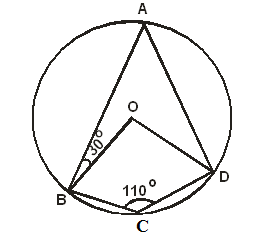
9. In the figure below ABCD is a cyclic quadrilateral. Point O is the centre of the circle. <ABO = 30^o and <BCD = 110^o.
                               
   Calculate the size of angle ADB.      (2 marks)

10. Three people Mutua, Wanza and Kiilu contributed money to start a business. Mutua contributed a quarter of the money and Wanza two fifths of the reminder. Kiilu’s contribution was one and a half times that of Mutua. They borrowed the rest of the money from a bank which was sh.60,000 less than Kiilu’s contribution. Find the total amount required to start the business. (4 marks)

11. Simplify (3 marks)
    

12. Expand (2-¹/₄x)⁵ and use the first three terms to find the value of 1.975⁵ to four significant figures.   (4 marks)

13. The radius of a spherical ball is measured as 7cm correct to the nearest centimeter. Determine to 2 decimal places, the percentage error in calculating the surface area of the ball. (3 marks)

14. Given that tan θ= ¹/_√5 where θ is an acute angle, find without using tables or calculator sin (90−θ) leaving your answer in the simplified surd form. (4 marks)

15. Given that a = 1.2, b = 0.02 and c = 0.2, express ac b in the form where m and n are integers.                   (3 marks)

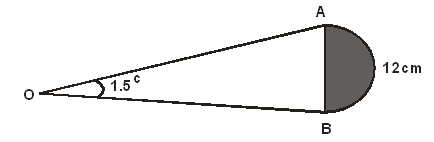
16. The diagram below shows sector AOB of a circle centre O. <AOB = 1.5^C and arc AB is of length 12cm.
    
    
    1. Determine the radius OA of the circle. (1 mark)
    2. Calculate the area of the shaded region. Give your answer correct to 3 s.f. (3 marks)

SECTION II (50 MARKS)

       Answer any FIVE questions from this section

17. The table below shows the taxation rates.
    

    Income (£ per month)	Rate (%)
    0-382	10
    383-754	15
    755-1126	20
    1127-1498	25
    1499-1870	30
    1871-2242	35
    over 2242	40

    Mueni is housed by her employer but pays a nominal rent of sh.1200 per month. She is entitled to a personal relief of sh.950 per month. If her monthly P.A.Y.E is sh.7024,
    1. Calculate her gross income. (5 marks)
    2. In addition to the tax the following monthly deductions are also made
       Sacco shares              Ksh. 1200
       Coop loan                   Ksh.1500
       Union dues                 Ksh.300
       Calculate
       1. Her monthly salary. (3 marks)
       2. Net monthly salary (2 marks)

18. Use a ruler and compasses only for all construction in this question.
    1. Construct a triangle ABC in which AB = 8cm, BC = 7.5cm and <ABC = 112¹/₂⁰ . (3 marks)
    2. Measure the length of AC. (1 mark)
    3. By shading the unwanted region show the locus of P within the triangle ABC such that AP BP, AP > 3cm. Mark the required region as P. (3 marks)
    4. Construct a normal from C to meet AB produced at D. (1 mark)
    5. Locate the locus of R in the same diagram such that the arc of triangle ARB is the arc of the triangle ABC. (2 marks)

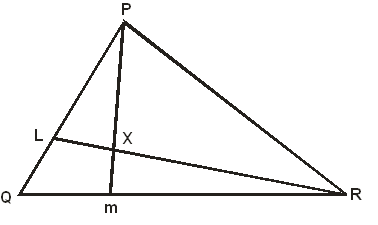
19. In the triangle PQR below, L and M are points on PQ and QR respectively such that PL : LQ = 1 : 3 and Qm : mR = 1 : 2. Pm and RL intersect at X. Given that PQ = b and PR= c
    
    
    1. Express the following vectors in terms of b and c.
       1. QR (1 mark)
       2. Pm (1 mark)
       3. RL (1 mark)
    2. By taking PX = hPm and RX = kRL where h and k are constants. Find two expressions of PX in terms of h, k, b and c. Hence determine the values of the constants h and k. (6 marks)
    3. Determine the ratio LX : XR. (1 mark)

20. OABC is a parallelogram with vertices O(0, 0), A(2, 0), B(3, 2) and C(1, 2). O^IA^IB^IC^I is the image of OABC under a transformation matrix.
    
    
    1.  
       1. Find the coordinates of O^IA^IB^IC^I                                     (2 marks)
       2. On the graph provided, draw OABC and O^IA^IB^IC^I             (2 marks)
    2.  
       1. Find O^IIA^IIB^IIC^II, the image of O^IA^IB^IC^I under the transformation matrix.  (2 marks)
          
       2. On the same grid, draw O^IIA^IIB^IIC^II. (1 mark)
    3. Find the single matrix that maps O^IIA^IIB^IIC^II onto OABC.                                     (3 marks)

21. An aircraft leaves town P (30^oS, 17^oE) and moves directly towards Q (60^oN, 17^oE). It then moved at an average speed of 300 knots for 8 hours Westwards to town R. Determine
    1. The distance PQ in nautical miles. (2 marks)
    2. The position of town R. (4 marks)
    3. The local time at R if local time at Q is 3.12p.m (2 marks)
    4. The total distance moved from P to R in kilometers. (Take 1nm = 1.853km) (2 marks)

22. The figure below is a sketch of a curve whose equation is y = x² + x + 5. It cuts the line y = 11 at points P and Q. 
                       
    1. Find the area bounded by the curve y = x² + x + 5 and the line y = 11 using the trapezium rule with 5 strips. (5 marks)
    2. Calculate the difference in the area if the mid-ordinate rule with 5 ordinates was used instead of the trapezium rule. (5 marks)

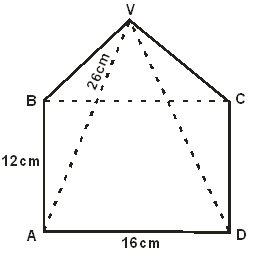
23. The figure below represents a rectangular based pyramid VABCD. AB = 12cm and AD = 16cm. Point O is vertically below V and VA = 26cm.
    
    Calculate:
    1. The height, VO, of the pyramid. (4 marks)
    2. The angle between the edge VA and the plane ABCD. (3 marks)
    3. The angle between the planes VAB and ABCD. (3 marks)

24. The distances S metres from a fixed point O, covered by a particle after t seconds is given by equation
    S = t³ – 6t² + 9t + 5
    1. Calculate the gradient to the curve at t = 0.5 seconds. (3 marks)
    2. Determine the values of S at the maximum and minimum turning points of the curve. (4 marks)
    3. On the space provided, sketch the curve of S = t³ – 6t² + 9t + 5. (3 marks)