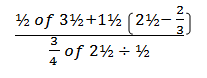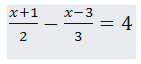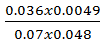MATHEMATICS PAPER 1 - 2019 LANJET JOINT MOCK EXAMINATION

SECTION 1 (50 MARKS)

Attempt all questions in this section.

1. If 2^x+y =16 and 4^2x-y = , find the value of x and y.                                                    (3mks)

2. The ratio of boys to girls in a school is 4:5. One day 1/3 of the boys and 1/5 of the girls were absent. If 8 less pupils had been absent, 3/4 of the school would have been present. Calculate the number of pupils in the school on that day.      (3mks)

3. Given that Cos A = 5/15 and angle A is acute, find the tan (90-A).       (2mks)

4. Tap A can fill a tank in 10 minutes; tap B can fill the same tank in 20 minutes. Tap C can empty the tank in 30 minutes. The three taps are left open for 5 minutes, after which tap A is closed. How long does it take to fill the remaining part of the tank?     (4mks)

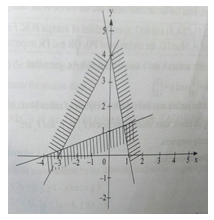
5. In the figure below, find the inequalities which describe the unshaded region.        (3mrks)
   
6. Without using a calculator evaluate;      (3 mks) 
                  

7. Simplify                   12x²  - 16x               (3 mks)
                                 20 – 11x – 3x²

8. Determine the equation of the line passing through (-1, 3) and parallel to the line whose equation is 3x-5y=10.(2mks)

9. A ship covers 60km on a bearing of 230⁰. It then changes its course and heads due west for 80km.Calculate its direct distance from the starting point.     (4mks)

10. Five shirts and four pairs of trousers cost sh 6160.  Three similar shirts and a pair of  trousers cost sh 2800.  Find the cost of four shirts and a pair of trousers.   (3mks)

11. A solid in a shape of a right pyramid on a square base of side 8cm and height 15cm is cut at 6cm height from the base. Find the volume of the frustrum formed. (4mks)

12. The sum of the interior angles of a regular polygon is 1080⁰
13.  
    1. Find the size of each exterior angle (2mks)
    2. Name the polygon.   (1mks)

13. A two digit number is such that the sum of the ones and the tens digit is ten. If the digits are reversed the new number formed exceeds the original number by 54. Find the number (3mks)

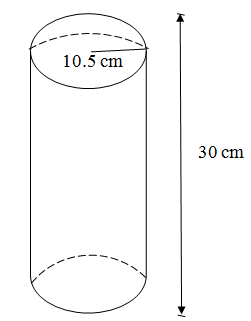
14. The solid shown below consists of a cylinder and hemisphere of equal radius 10.5cm. If the height of the solid is 30cm. find its surface area. (Take π= 22/7)            (4mks)
    

15. Solve the equation    (3 mks)
    

16. Evaluate without using tables or calculator;                                                                    (3mks) 
    

SECTION II:  (50MARKS).
Attempt any five questions in this section.

17. Using a ruler and a pair of compass only;
    1. Construct triangle ABC in which AB=5cm, BC=5.9cm and angle BAC=45⁰         (4mks)
    2. Draw an incircle of the triangle ABC and measure its radius.                       (3mks)
    3. By taking AB as the base, find the area of the triangle.                                 (3mks)

18. Three warships P, Q and R are at sea such that ship Q is 400km on a bearing of 030⁰ from      ship P. Ship R is 750 km from ship Q and on a bearing of 120⁰ from ship Q. An enemy ship S is sighted 1000km due south of ship Q. 
    1. Taking a scale of 1cm to represent 100km, locate the relative positions of ships P, Q, R and S.                                                                                                    (4mks)
    2. Find the compass bearing of;
       1. P from S                                                                                            (2 mks)
       2. S from R                                                                                
    3. Use the scale drawing to determine the distance of:
       1. S from P                                                                                              (2 mks)
       2. R from S
    4. Find the bearing of:
       1. Q from R                                                                                             (2 mks)
       2. P from R
19. Two friends Jane and Tom live 40km apart. One day Jane left her house at 9:00am and cycled towards Tom’s house at an average speed of 15km/hr. Tom left his house at 10.30am           on the same day and cycled towards Jane’s house at an average speed of 25km/hr.
    1. Determine:
       1. The distance from Jane’s house to where the two friends met.          (4mks)
       2. The time they may                                                                              (2mks)
       3. How far Jane was from Tom’s house when they met.                        (2mks)
    2. The two friends took 10 minutes at the meeting point and then cycled to Tom’s house at an average speed of 12km/hr. Find the time they arrived at toms house.                                                                                                                            (2mks)

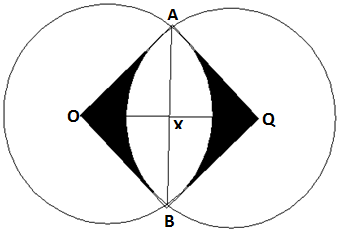
20. Two equal circles with centres O and Q and radii 8cm intersect at points A and B as shown below.  Given that the distance between O and Q is 12cm and that line AB meets OQ at X.
    
    Find;
    1. The length of chord AB.                                                                                 (2mks)
    2. The area of the shaded region.                                                                        (6mks)
    3. The reflex angle AOB.                                                                                    (2mks)

21. A kite ABCD has vertices at A(1,1), B(6,2), C(6,6) and D(2,6).
    1. On the axes draw the image and state its coordinates;                                        
       1. A’B’C’D’ of ABCD under a rotation of 90⁰ about the origin.                (3 mks)
       2. A’’B’’C’’D’’ of A’B’C’D’ under a reflection in the line y=x.               (3mrks)
       3. A’’’B’’’C’’’D’’’ of A’’B’’C’’D’’ under a reflection in the line x=0.      (2mks)
    2. Describe a single transformation that maps A"B"C"D onto ABCD.                   (2mks)

22. A triangular plot ABC is such that AB=72m, BC=80m and AC=84m.
    1. Calculate the:
       1. Area of the plot in square meters.                                                             (3mks)
       2. Acute angle between the edges AB and BC.                                          (3mks)
       3. Perpendicular height from A to the line BC.                                            (2mks)
    2. A water tap is to be installed inside the plot such that the tap is equidistant from each of the vertices A,B and C. Calculate the distance of the tap from the vertex A. (2mks)
23.  
    1. Find the equation of a straight line passing through the point (3, 2) and (-3, 6) giving your  in the form + =1 where a and b are constants.  (4mks)
    2. State the coordinates of points A and B at which the line in (a) above crosses the x-axis and y-axis respectively.                                                                                  (2mks)
    3. Using the information in (a) and (b) above, find the area of triangle AOB where O is the origin.                                                                                                            (2mks)
    4. Find the acute angle the line in (a) above makes with the x-axis.                    (2mks)

24. A flag post 12m long is fixed on top of a tower. From a point on horizontal ground, the angles of elevation of the top and bottom of the flag post are 46 ⁰ and 33⁰ respectively.   
    Calculate;
    1. The horizontal distance from the point on the ground to the base of the tower. (4mks)
    2. The total height of the tower and the flag post.                                                   (2mks)
    3. The shortest distance from the point on the ground to
       1. The top of the flag post.                                                                           (2mks)
       2. The top of the tower.                                                                          (2 mks)