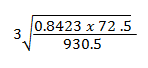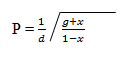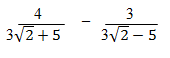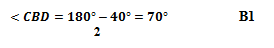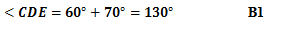SECTION 1 (50 MARKS)
Attempt all questions in this section.
- Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm (3mks)
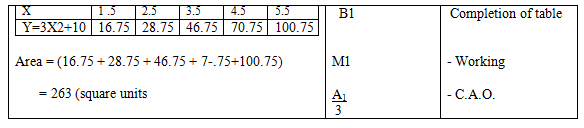
- Using the mid-ordinate rule of 5 strips, determine the area under the curve y = 3x2 + 10. The lines x = 1, x = 6 and x-axis. (3 mks)
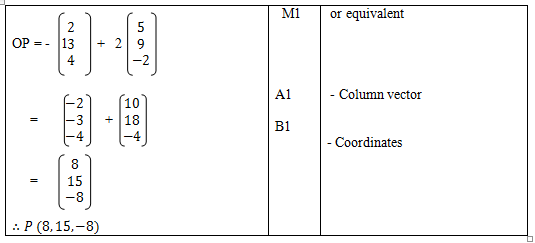
- OA = 2i + 3j + 4k while OB = 5i + 9j – 2k. P divides AP externally in the ratio 2:1. Find the coordinates of P. (3 mks)
- Use mathematical tables to evaluate: (4mks)
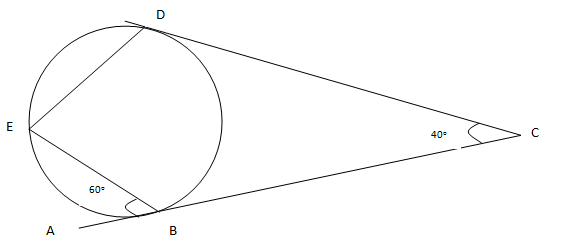
- On the figure below, line ABC and DC are tangents of the circle at B and D respectively.
Calculate- <CBD
- <CDE
- Without using a calculator evaluate; (3mks)
(log2 x )2 + log2 8 = log 2 x4
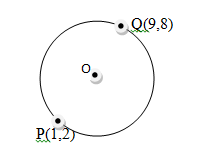
- P and Q are the points on the ends of the diameter of the circle below.
- Write down in terms of X and Y the equation of the circle in the form:
ax2 + by2 + x + y + c = 0 (2 mks) - Find the equation of the tangent at Q in the form ax + by + c = 0 (2 mks)
- Write down in terms of X and Y the equation of the circle in the form:
- Solve the equation 4 – 4cos2 x = 4Sin x-1 for the range 0 (3 mks)
- Expand (1 - 1/2x9 )up to the fourth term, hence use your expansion to evaluate 0.9959, correct to 4 decimal places. (4 mks)
- Make x the subject of the formula (3 mks)
- Solve the following quadratic equation by completing the square method. Give your answer to one decimal place. (3 mks)
2x2 – 7x + 2 = 0
-
- Given that P =
and 0 =
Find PO(1 mk)
- Hence, find the point of intersection of the lines 4x + y = 9 and 3y = 2x – 1. (2 mks)
- Given that P =
- Two types of tea which cost Ksh 200 per kg and Kshs 250per kg are mixed so that their
weights are in the ratio 5:3 respectively. Calculate the cost of 20kg of the mixture. (3 mks)
- Expand the expression
(3 mks)
- T is a transformation represented by the matrix
. Under T, a square of area of 18cm2 is mapped onto a square of area 110cm2. Find the value of x. (3 mks)
- After how many years would Khs 15,000 amount to Kshs 24,015.50 at a rate of 16% p.a compounded quarterly? (3 mks)
SECTION II (50 MARKS)
Answer only FIVE questions in this section in the spaces provided.
- The table below shows the Kenya tax rates in a year
Income (Ksh per annum)
Tax rate (per £)
1 – 116,160
10%
116,161 – 225,600
15%
225,601 – 335,040
20%
335,041 – 444,480
25%
Over 444,481
30%
In that year, Ushuru earned a basic salary of Ksh 30000 per month. In addition, he was entitled to a medical allowance of Ksh 2,800 per month and a traveling allowance of Ksh 1800 per month. He is housed by the employer and pays a nominal rent of 2000. He also claimed a monthly family relief of Ksh 1056. Other monthly deductions were union dues Ksh 445, WCPS Ksh 490, NHIF Ksh 320, COOP shares Ksh 1000 and risk fund Ksh 100
Calculate:- Ushuru’s annual taxable income. (2marks)
- The tax paid by Ushuru in that year. (5marks)
- Ushuru’s net income in that year (3marks)
- The marks of 50 students in a mathematics test were taken from a form 4 class and recorded in the table below.
Marks (%) 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 Frequency 2 5 7 9 11 8 5 3 - On the grid provided, draw a cumulative frequency curve of the data. (3marks)
- From your curve in (a) above
- Estimate the median mark. (1mark)
- Determine the Interquartile deviation. (2marks)
- Determine the 10th to 90th percentile range. (2marks)
- It is given that students who score over 45 marks pass the test. Use graph in (a) above to estimate the percentage of students that pass. (2marks)
-
- The first term of a G.P is 4. If the common ratio is 2, find the greatest number of terms that will give a sum less than 40 (4marks)
- The 2nd , 4th and 7th terms of a A.P are the first 3 consecutive terms of a G.P. if the common difference of AP is 2 Find
- The common ratio (3marks)
- The sum of the first eight terms of the G.P. (3marks)
- An aeroplane flies from a point P(600N, 450W) to a point Q(600N, 1350E). Given that the radius of the earth is 6370km,
- Calculate the shortest distance between P and Q:
- In kilometres (km) (3marks)
- In nautical miles (nm) (1mark
- If the plane flew at a speed of 600 knots, how long did it take to move from P to Q? (2 marks)
- The plane left P at 10.00a.m on Monday. At what time did it arrive at Q if it travelled along a parallel latitude at the same speed.
- Calculate the shortest distance between P and Q:
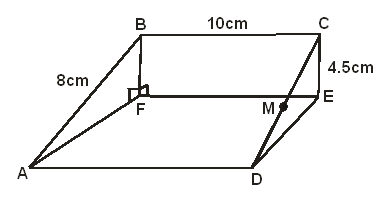
- The above diagram represents a wooden prism. ABCD is a rectangle. Points E and F are directly below C and B respectively. M is the midpoint of CD. AB = 8cm, BC= 10cm and CE= 4.5cm.
- Determine the size of angle CDE. (2marks)
- Calculate:
- Length of AC. (2marks)
- The angle CAE makes with the plane ADEF. (2marks)
-
- Find the:Length of MB. (2marks)
- Angle CBM. (2marks)
- The probability that a school team will win a match is 0.6. The probability that the team will loose the match is 0.3 and the probability that the team will draw in the match is 0.1. Given that the team will play two matches.
- Draw a tree diagram to represent the above information. (2marks)
- What is the probability that the team will
- Win the two matches (2marks)
- Either wins all the matches or losses all the matches? (2marks)
- Wins one match and losses one (2 marks)
- Tie in one match. (2 marks)
- Three variables p, q and r are such that p varies directly as q and inversely as the square of r.
- When p = 18, q = 24 and r = 4.
Find p when q = 30 and r = 10. (4marks) - Express q in terms of p and r. (1mark)
- If p is increased by 20% and r is decreased by 10% find:
- A simplified expression for the change in q in terms of p and r. (3marks)
- The percentage change in q. (3marks)
- When p = 18, q = 24 and r = 4.
-
- Using a ruler and pair of compasses only construct triangle ABC in which AB = 6.5cm, BC= 5.0cm and angle ABC = 600. Measure AC (3marks)
On same side of AB as C - Determine the locus of a point P such that angle APB = 600 (3marks)
- Construct the locus of R such that AR = 3cm. (1mark)
- Identify the region T such that AR³ 3 and ÐAPB³ 600 by shading the unwanted part. (3marks)
- Using a ruler and pair of compasses only construct triangle ABC in which AB = 6.5cm, BC= 5.0cm and angle ABC = 600. Measure AC (3marks)

MARKING SCHEME
- Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm (3mks)
- Using the mid-ordinate rule of 5 strips, determine the area under the curve y = 3x2 + 10. The lines x = 1, x = 6 and x-axis. (3 mks)
- OA = 2i + 3j + 4k while OB = 5i + 9j – 2k. P divides AP externally in the ratio 2:1. Find the coordinates of P. (3 mks)
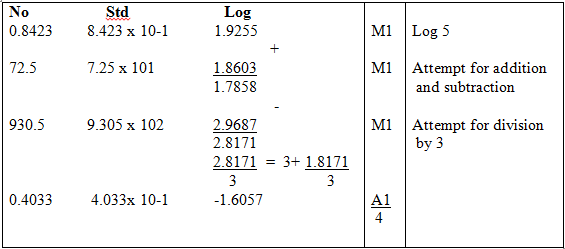
- Use mathematical tables to evaluate: (4mks)
- On the figure below, line ABC and DC are tangents of the circle at B and D respectively.
Calculate- <CBD
- <CDE
- <CBD
- Without using a calculator evaluate; (3mks)
(log2 x )2 + log2 8 = log 2 x4
Download MATHEMATICS PAPER 2 - 2019 LANJET JOINT MOCK EXAMINATION.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students