MATHEMATICS PAPER 2 - KCSE 2019 MARANDA MOCK EXAMINATION

SECTION   I (50 MKS)
Answer ALL questions in this section in the spaces provided.

1. Use logarithms to evaluate      (4mks)
   

2. Factorise completely;     (2mks)
   45 - 5x²

3. Find all the integral values of x which satisfy the inequalities.
   3(3-x) ˂ 5x – 9 ˂ 2x + 8         (4mks)
4.  
   1. Expand   (1 – 2x)⁶ in ascending powers of x up to x³   (2mks)
   2. Hence evaluate   (1.02)⁶ to 4 d.p.   (2mks)

5. Given that a = b +√(b² +c² ) make c the subject of the formula     (3mks)

7. Find the radius and centre of a circle whose equation is   x² +   y² +   3x   +   2   =   0   (3mks)

8. The difference between the exterior and interior angle of a regular polygon is 100^o. Determine the number of sides of the polygon     (3mks)

9. In the figure below, line CD = 4cm, line DT = 8cm and AB = 6cm. AT and CT are straight lines meeting at point T.
   Find the value of y   (3mks)
   

10. The sides of a square are decreased by 5%. By what percentage is the area decreased? (2mks)

11. It would take 18men 12 days to dig a piece of land. If they work for 8 hours a day, how long will it take 24 men working 12 hours to cultivate three quarters of the same land?   (3mks)

12. A ship P is due south of the lighthouse L. A ship Q is 4.8km due East of L. The bearing of Q from P is 030^o. P sails directly towards Q. Find the distance of P from L when its bearing from L is 110^o (3mks)

13. Calculate the percentage error in the volume of a cone whose radius is 9.0cm and slant length 15.0cm   (4mks)

14. A coffee dealer mixes two brands of coffee, x and y to obtain 40kg of the mixture worth Ksh. 2,600. If brand x is valued at Ksh. 70 per kg and brand y is valued at ksh, 55 per kg. calculate the ratio in its simplest form in which brands x and y are mixed (4mks)

15. A man deposits   kshs. 50,000 in an investment account which pays 12% interest p.a. compounded semi-annually. Find the amount in the account after 3 years. (3mks)

16. Find without using log tables or calculators the value of x which satisfies the equation Log₃(x² – 9)  =  2log₃ 3 +   1                     (3mks)
    
    SECTION   II ( 50 MKS )
    ANSWER ANY 5 QUESTIONS IN THIS SECTION IN THE SPACES PROVIDED 
17. A triangle ABC has the vertices A(-5,-2), B(9-3,-2) and C(-5,-5)   The triangle is rotated through a positive quarter turn about the origin to obtain the image A’B’C’. The triangle A’B’C’ is then reflected on the line y + x = 0 to get triangle A”B”C”
    1. On the grid provided, plot triangle ABC, A’B’C’ and A”B”C”   (4mks)
    2. Describe a single transformation that maps ABC onto A”B”C” and the matrix of transformation (3mks)
    3. Find the coordinates of the image of ABC under a stretch, scale factor 2 parallel to the x – axis and y-axis invariant (3mks)

18. The product of the first three terms of a geometric progression is 64. If the first term isa and the common ration is r;
    1. Express r in terms of a   (3mks)
    2. Given that the sum of the three terms is 14. Find the values of a and r and hence write down two possible sequences each up to the 4^thterm (5mks)
    3. Find the product of the 50^th terms of the two sequences.   (2mks)

19. The probabilities ofMaina, Omondi and Wambua scoring 80 percentage are ¾, 2/3, and 4/5 respectively. Find the probability that:-
    1. All the three candidates will pass (2mks)
    2. all the three candidates will not pass   (2mks)
    3. Only one of them will pass (2mks)
    4. Only two of them will pass (2mks)
    5. At most two of them will pass   (2mks)

20. In the trapezium below, PQ = 3ST, T divides SR in the ratio   4:1 and U is the mid point of QT, PU and QR interest at X. PX = hPU and QX = KQR. Given that PQ = q and PS = p:
    
    
    1. Express   QR  in terms of   p and q     (1mk)
    2. Express   PX in terms of p, q and h   (2mks)
    3. Express   PX in terms of p, q and K   (3mks)
    4. Hence obtain the values of h and k   (3mks)
    5. Determine the ratio in which X divides QR (1mk

21. given that y = 2sin 2x and y = 3cos (x + 45^o):
    1. complete the table below   (2mks)
       

       X	00	200	400	600	800	1000	1200	1400	1600	1800
       2sin 2x	0		1.97		0.68	-0.68	-1.73		-1.28	0.00
       3cos (x+450)	2.12	1.27		-0.78		-2.46			-2.72	-2.12

    2. Use the data to draw the graphs of y = 2sin 2x and y = 3cos(x + 45^o) for   0^o≤ x   ≤ 180^oon the same axes   (4mks)
    3. State the amplitude and period of each curve.   (2mks)
    4. Use the graph to solve the equation
       2sin 2x – 3cos(x + 45^o) = 0, for   0^o≤ x   ≤ 180^o   (2mks)

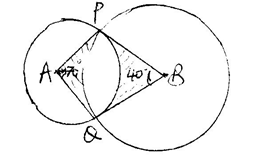
22. The diagram below shows two circles centre A and B which intersect at point P and Q. Angle PBQ = 40^o and angle PAQ =  70^o and PA = AQ =   8cm. Use the diagram to calculate to 2d.p.
    
    
    1. The length PQ   (2mks)
    2. The length PB   (2mks)
    3. Area of the minor segment of circle centre A.   (2mks)
    4. Area of minor segment of circle centre B   (2mks)
    5. The area of shaded region   (2mks)
23.  
    1. using a ruler and a pair of compasses only construct;
       1. Triangle ABC, such that AB = 9cm, AC = 7cm and angle   CAB =   60^o.   (2mks)
       2.  the locus of P, such that AP   ≤ BP   (2mks)
       3. the locus of Q such that   CQ≤   3.5cm   (2mks)
       4. locus of R such that angle ACR≤ angle   BCR   (2mks)
    2. Find the area of the region satisfied by both P and Q   (2mks)

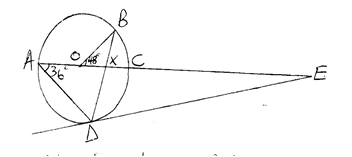
24. In the figure below, O is the centre of the circle, A,B,C and D are points on the circumference of the circle.   A, O, X and C are points on a straight line. DE is a tangent to the circle at D. Angle BOC = 48^o and CAD =   36^o
    
    
    1. Giving reasons in each case, find the value of the following angles
       1. Angle CBA       (2mks)
       2. Angle BDE     (2mks)
       3. Angle   CED     (2mks)
    2. It is also given that AX = 12cm, XC = 4cm and DB = 14cm and DE = 15cm. Calculate ;
       1. DX     (2mks)
       2. AE   (2mks)