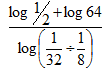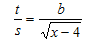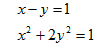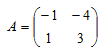MATHEMATICS PAPER 2 - KCSE 2019 BAHATI MOCK EXAMINATION (WITH MARKING SCHEME)

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

1. Evaluate without using tables or calculators. (3 marks)
   

2. Make x the subject of the equation (3 marks)   
        

3. Two pipes, P and Q can fill an empty tank in 3 hours and 4 hours respectively. It takes 5 hours to fill the tank when an outlet pipe R is opened the same time with the inlet pipes. Calculate the time pipe R takes to empty the tank. (3 marks)

4. Given that M=i – 3j + 4k, W= 6i + 3j – 5k and Q = 2M + 5N, find the magnitude of Q to 3 significant figures. (3 marks)    

5. A triangle ABC is such that a =14.30 cm, b =16.50 cm and B =56º. Find the radius of a circle that circumscribes the triangle.             (3 marks)

6. Construct a circle centre O and radius 3 cm. Construct two tangents from a point T, 6.5 cm from O to touch the circle at W and X. measure Angle WTX. (3 marks)

7. Grace deposited Ksh 16 000 in a bank that paid simple interest at the rate of 14% per annum. Joyce deposited the same amount of money as Grace in another bank that paid compound interest semi- annually. After 4 years, they had equal amounts of money in the banks.
   Determine the compound interest rate per annum, to I decimal place, for Joyce’s deposit.(4 marks)                      

8. Simplify,  leaving your answer in the form,  where a, b, and c are integers. (2 marks)

9. Solve the equation (4marks)
   

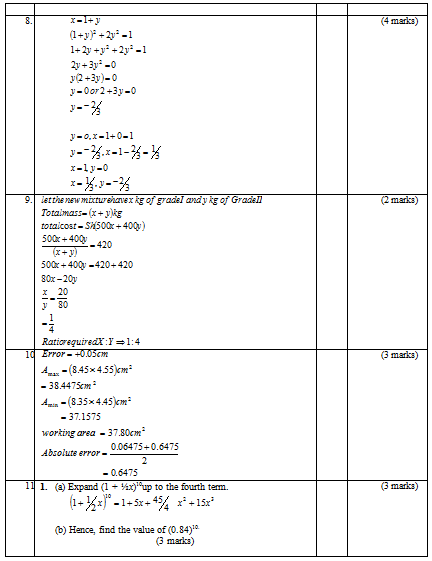
10. Grade I coffee cost sh 500 per kilogram while grade II coffee costs sh 400 per kilogram. The grades are mixed to obtain a mixture that costs sh 420 per kilogram. In what ratio should the two grades be mixed?(3 marks)      

11. The base length and height of parallelogram were measured as 8.4 cm and 4.5 cm respectively. Calculate the maximum absolute error in the area of the parallelogram. (3 marks)

12.  
    1. Expand (1 + ½x)¹⁰up to the fourth term.
    2. Hence, find the value of (0.84)^10.      (3 marks)

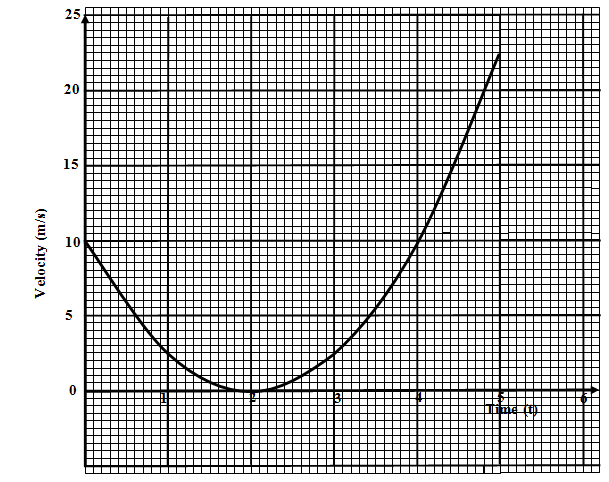
13. The graph below shoes the relationship between velocity of a body and time (t) seconds in the interval  0 ≤ t = 5. 
    
    Use the graph to determine ;
    1. the average rate of change of velocity between t = 2.5 seconds and t = 5 seconds.        (2 marks)
    2. the instantaneous rate of change at t = 4 seconds.                                                            (2 marks)

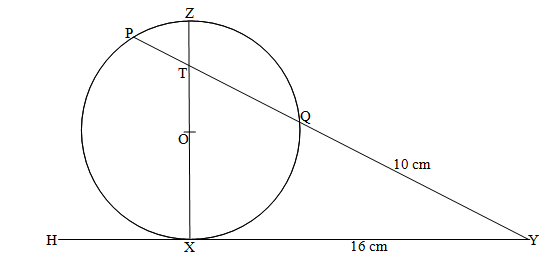
14. In the figure below, the tangent HXY meets chord PQ produced at Y. Chord XZ passes through the centre, O, of the circle and intersects PQ at T. Line XY = 16 cm and QY = 10 cm. 
    
    
    1. Calculate the length PQ.        (2 marks)
    2. If ZT = 4 cm and PT: TQ = 3:5, find XT.     (2 marks)

15. Quantity P varies partly as Q and partly varies inversely as square of When Q = 1, P = 1 and when Q = ½, P = -3. Find the equation of the relationship connecting P and Q. (3 marks)

16.  A point Q divides line AB externally the ratio 5:2. Find the position vector of point Q. (3 marks)

SECTION II (50 Marks)
Answer any five questions from this section.

17. Two tanks of equal volume are connected in such a way that one tank can be filled by pipe A in 1hour 20minutes. Pipe B can drain one tank in 3hours 36minutes but pipe C alone can drain both tanks in 9 hours. Calculate:
    1. The fraction of one tank that can be filled by pipe A in one hour.                                     (2mks)
    2. The fraction of one tank that can be drained by both pipes B and C in one hour.             (4mks)
    3. Pipe A closes automatically once both tanks are filled. Assuming that initially both tanks are empty and all pipes opened at once, calculate how long it takes before pipe A closes.     (4mks)

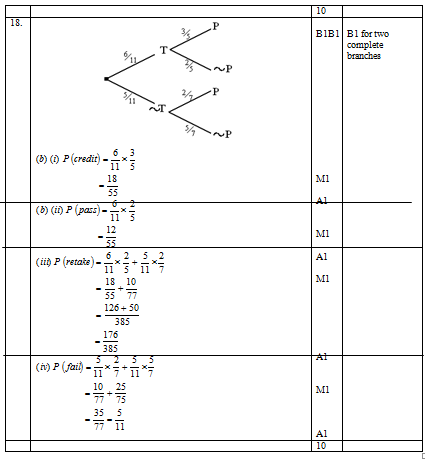
18. An examination involves a written test and a practical test. The probability that a candidate passes the written test is 6/₁₁ if the candidate passes the written test, then the probability of passing the practical test is 3/₅ , otherwise it would be 2/₇ 
    1. Illustrate this information on a tree diagram.                                                                     (2mks)
    2. Determine the probability that a candidate is awarded
       1. Credit for passing both tests.                                                                                        (2mks)
       2. Pass for passing the written test.                                                                                   (2mks)
       3. Retake for passing one test.                                                                                          (2mks)
       4. Fail for not passing the written test.                                                                             (2mks)

19.  
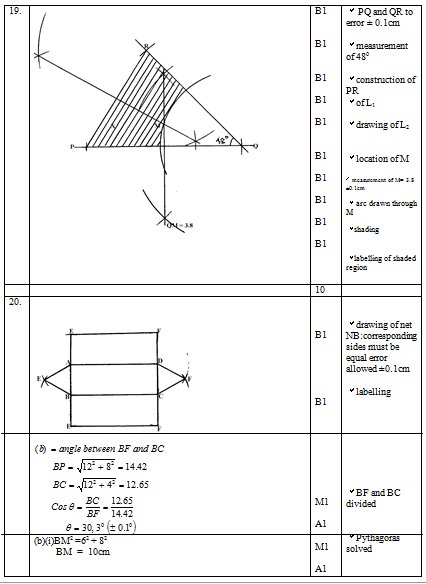
    1. Conctruct triangle PQR with PQ = 7.2cm, QR = 6.5cm and angle PQR = 48⁰  (3mks)
    2. The locus L1, of points equidistant from P and Q, and locus , L2 of points equidistant from P and R, meet at M. Locate M and measure QM    (4mks)
    3. A point x moves within triangle PQR such that QX ≥ QM Shade and label the locus of X. (3mks)

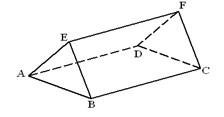
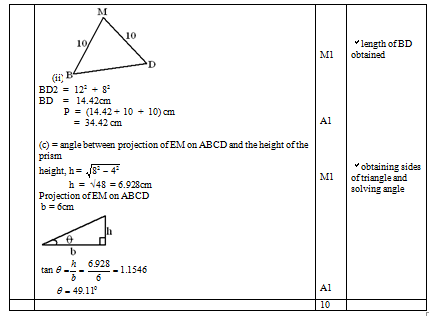
20. The figure below represents a prism with a cross section of an equilateral triangle of side 8cm and length 12cm, as shown below.
    
    
    1. Draw the net of the prism ABCDEF                                                                                      (2mks)
    2. Calculate the angle between the plane ABCD and the line BF.                                           (2mks)
    3. M is the midpoint of EF. Calculate
       1. The length BM                                                                                                                (2mks)
       2. The perimeter of triangle BMD.                                                                                       (2mks)
    4. Calculate the angle between the plane ABM and the base plane ABCD.                           (2mks)

21. Give the matrix 
    1. Calculate A² and A³                                                                                               (2mks)
    2. Find the values of the constants p and q for which A² = pA + qI where I is the identity matrix.  (3mks)
       
    3. The triangle ABC maps onto A¹B¹C¹ under the transformation represented by matrix A. Find the area of triangle ABC if the area of triangle A¹B¹C¹ is 21cm² (3mks)                   
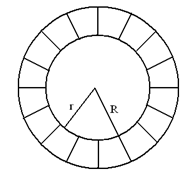
    4. The figure shows two concetric circles such that the ratio of their radii is 1: 3. If the area of the shaded region is 78.4 square units, calculate the area of the larger circle.  (2mks)
22. A certain uniform supplier is required to supply two types of shirts: one for girls labelled G and the other for boys labelled B. The total number of shirts must not be more than 400. e as to supply more of type G than of type B. However the number of type G shirts must not be more than 300 and the number of type B shirts must not be less than 80. by taking x to be the number of type G shirts and y the number of type B shirts,
    1. Write down in terms of x and y all the inequalities representing the information above.                                                                                                                   (3mks)
    2. On the grid provided draw the inequalities and shade the unwanted regions.   (4mks)
       Given that type G costs Shs. 500 per shirt and type B costs Shs. 300 per shirt.
       1. Use the graph in (b) above to determine the number of shirts of each type that should be made to maximize profit. (1mk)
       2. Calculate the maximum possible profit.     (2mks)
23.  
    1. The equation of a curve is given by y = X³ + X² – bx. Show that the value of X at the  minimum turning point is (3mks)
    2. The displacement X metres of a particle moving along a straight line after t seconds is given by X = 4t + 2t² – t³
       1. Find its initial acceleration            (2mks)
       2. Calculate the time when the particle was momentarily at rest.                                     (2mks)
    3.  
       1. Find the values of X where the curve y = X² (x - 2)  crosses the x-axis.                               (1mk)
       2. Hence find the area enclosed by the curve y = X² (x - 2), the lines x = 0, x = 2 2/₃  and the x-axis.                         (2mks)

24. The marks of 50 students in a mathematics test were taken from a form 4 class and recorded in the table below.
    

    Mark (%)	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
    Frequency	2	5	7	9	11	8	5	3

    
    
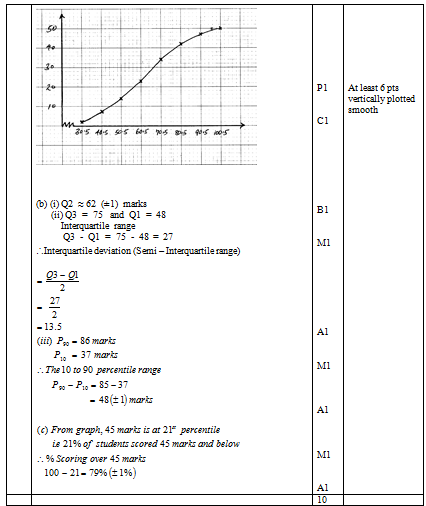
    1. On the grid , draw a cumulative frequency curve of the data.                             (3mks)
       
       Take: 1cm to represent 5 students on the vertical scale and 1cm to represent 10 marks on the         horizontal scale.
    2. From your curve in (a) above
       1. Estimate the median mark.                                                                                   (1mk)
       2. Determine the Interquartile deviation.                                                                (2mks)
       3. Determine the 10^th to 90^th percentile range.                                                        (2mks)
    3. It is given that students who score over 45 marks pass the test. Use graph in (a) above to estimate the percentage of students that pass.   (2mks)

MARKING SCHEME