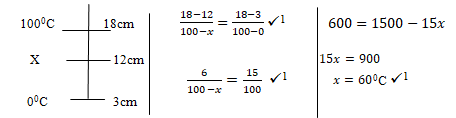INSTRUCTION TO CANDIDATES
- This paper consists of TWO sections: A and B
- Answer ALL questions in section I and II in the spaces provided.
- ALL workings MUST be clearly shown.
- Mathematical tables and electronic calculators may be used.
SECTION A (25 Marks)
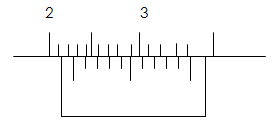
- Figure below shows part of a scale of a vernier calipers. What is the reading indicted by the scale? (2 marks)
- A horse pipe of internal diameter 4 cm is connected to a sprinkler with 25 holes each of diameter 0.04 cm, the water in the pipe flows at a speed of 5 cm/s. Determine the velocity with which the water leaves the sprinkler. (3 marks)
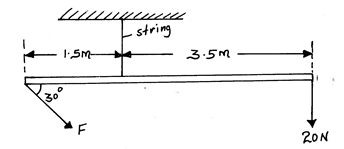
- The figure below shows a uniform bar of weight 8N. It is acted on by two forces as shown.
Determine the value of F. (3 marks)
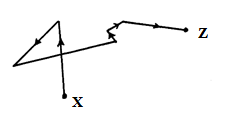
- The figure below shows a path taken by a gas molecule moving from point x to z
- Explain how this movement can be observed (1 mark)
- State in full, the law of motion that governs movement from x to z (1 mark)
-
- State one factor that a bimetallic strip relies on for its working (1 mark)
- Two objects made of the same material and having the same mass are heated to a temperature of 35oC above that of the atmosphere and then allowed to cool in still air for 30 minutes. State one factor that will determine their final temperature (1 mark)
-
- What is surface tension? (1 mark)
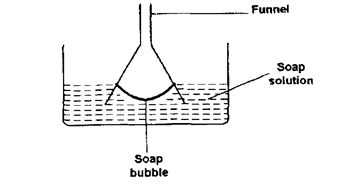
- The figure below shows a funnel dipped into a liquid soap solution.
Explain what happens to the soap bubble when the funnel is removed. (2 marks)
- A solid displaces 8.5cm3 of liquid when floating on a certain liquid and 11.5cm3 when fully submerged in the liquid. The density of the solid is 0.8g/cm3, determine upthrust on the solid when it is floating (3 marks)
- Fifty drops of oil have a volume of 1.0cm3. If a drop of oil forms an oil patch of diameter 20cm, determine the size of the oil molecule. (2 marks)
- In a faulty mercury-in-glass thermometer was found that the mercury level stands at 3 cm mark in the tube at 00 C and 18 cm when in steam above boiling water at normal atmospheric pressure. Calculate the temperature when the mercury stands at 12 cm mark. (3 marks)
- Give two reasons why mercury is preferred to water in the manufacturing of barometers(2 marks)
SECTION B (55 Marks)
-
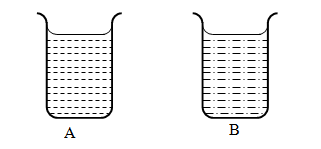
- The figure below shows two containers filled with two different liquids to the same height. It was found that the pressure at the bottom of A is greater than that at B.
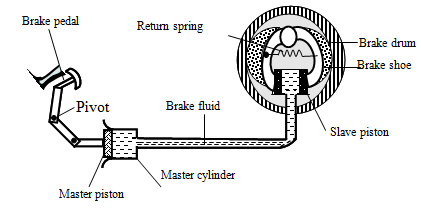
Explain (1 mark) - The figure below shows a car braking system. The brake fluid is an oily liquid. The brake drum rotates with the wheel of the car.
-
- Explain how pushing the brake pedal makes the brake rub against the drum. (4 marks)
- The cross-sectional area of the master piston is 2.0cm2. A force of 140N is applied to the master piston.
- Calculate the pressure created in the brake fluid by the master piston. (2 marks)
- The cross-sectional area of each slave piston is 2.8cm2. Calculate the force exerted on each slave piston by the brake fluid. (2 marks)
- The force exerted on the master piston is greater than the force applied by the foot on the brake pedal. Using the principle of moments, explain this. (2 marks)
- The figure below shows two containers filled with two different liquids to the same height. It was found that the pressure at the bottom of A is greater than that at B.
-
- State two factors that affect the magnitude of centripetal force of an object moving along a curved path. (2 marks)
- A stone is tied to a light string of length 0.5m. If the stone has a mass of 20g and is swung in a vertical circle with a uniform angular velocity of 6 revolutions per second, determine.
- The period T. (2 marks)
- The tension of the string when the stone is at
- The bottom of the swing. (3 marks)
- The top of the swing. (2 marks)
- The linear velocity. (3 marks)
-
- Define the term uniform acceleration. (1 mark)
- A rocket was launched vertically upwards with uniform acceleration of 100ms-2 for 20 seconds. After this the rocket was acted upon only by a constant gravitational force.
- Calculate the maximum height reached by the rocket (3 marks)
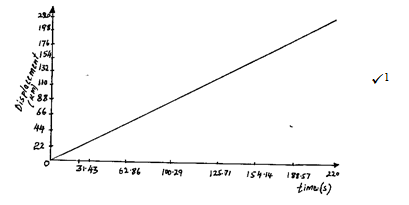
- Draw to scale, on the axes provided below, the displacement – time graph for the motion of the rocket. (2 marks)
- State Newton’s second law of motion. (1 mark)
- A car of mass 800Kg is initially moving at a speed of 25m/s. Calculate the constant force required to bring the car to rest over a distance of 20m. (4 marks)
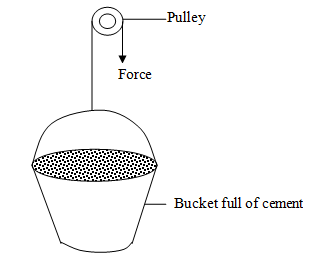
- A worker on a building site raises a bucket full of cement at a slow steady speed using the pulley as shown below.The weight of the bucket and cement is 200N. The force F exerted by the worker is 210N
- State why F is bigger than the weight of the bucket and cement. (1 mark)
- The bucket is raised through a height by 4m. Determine the distance through which the worker pulls the rope. (1 mark)
- How much work is done on the bucket and cement? (2 marks)
- State the kind of energy gained by the bucket. (1 mark)
- Determine the total work done be the worker. (3 marks)
- Calculate the efficiency of the machine used by the water. (2 marks)
-
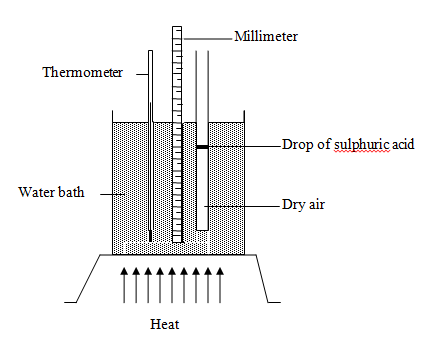
- The figure below shows a set-up that may be used to verify Charles’ law.
- State the measurements that should be taken in the experiment. (2 marks)
- Explain how the measurements taken in (i) above may be used to verify Charles’ law. (2 marks)
- A certain mass of hydrogen gas occupies a volume of 1.6cm3 at a pressure of 1.5 x 105 pa and temperature of 12o Determine its volume when the temperature is 0oC at a pressure of 1.0 x 105 pa. (2 marks)
-
- An electric kettle connected to a 250V mains supply draws a current of 4.0A. It contains 1 litre of water with 1 kg of ice, all at 00C. Neglecting all heat losses, including heat absorbed by the kettle, find the time taken for all the ice to be just melted. (Take specific latent heat of fusion to be 3.34 x 105 J/kg and latent heat of vaporization is 2.26 x 106 J/kg Specific heat capacity of water is 4.2J/g). (2 marks)
- Determine the time taken until half the contents of the kettle boils away
- The figure below shows a set-up that may be used to verify Charles’ law.

MARKING SCHEME
SECTION A
- Main scale reading = 2.10 cm
Vernier scale reading = 0.05 cm
Reading on the scale = 2.15 cm.
- A1U1 = A2U2
π x 2 cm x 2 xm x 5cm/s = π x 0.02cm x 0.02cm x 25 x U2cm/s
Make U2 to get that U2 = 2,000 cm/s
- Clockwise moments = Anti clockwise moments;
(20x3.5) + (8x2.5) = F sin 30 x 1.5;
70 + 20 = 0.5 F x 1.5
90/1.5 = 0.5 F
60 = 0.5 F
F = 60/0.5 = 120N
-
- By strongly illuminating a suspension of pollen grains in water/dust particles in air or smoke cell
- A body continues in its state of rest or motion with uniform velocity unless acted upon by an external force
-
- Difference in expansion rates of materials
- Surface Area to Volume ratio
-
- Surface tension is the force per unit length acting on the surface of a liquid and perpendicular to one side of an imaginary line drawn in the surface.
- Bubble flattens to form a film and moves up the funnel in order to make its surface area be as small as possible due to surface tension
- Surface tension is the force per unit length acting on the surface of a liquid and perpendicular to one side of an imaginary line drawn in the surface.
- Up thrust = weight of solid
= ℓvg
= 800kg/m3 x (115 x 10-6) m3 x 10N/Kg
= 0.092 N
- 50 drops = 1.0 cm3
Hence, 1 drop = 0.02 cm3
Volume = Area x Thickness
Thickness = 6.37x10-1 m -
-
- Mercury is denser, hence rises to reasonable heights
- Due to great cohesion forces between mercury molecules, it does not stick on the glass surface.
SECTION B
-
- Liquid A is denser than liquid B.
-
- When the pedal is pushed, pressure is generated in the master cylinder; This pressure is transmitted to the slave cylinder; This causes the pistons of the slave cylinder to open the brake shoe and hence the brake lining presses the drum.
- P = 700,000N/m2
- F = P x A = 700,000 x 2.8 x 10-4 = 1,960N
- Distance from the foot to pivot is larger than piston to pivot;
Force x distance = Constant
- Liquid A is denser than liquid B.
-
- -Radius of path
-Mass of the object
-Linear speed. -
- The period T.
T =1/F
= 1/6
= 0.1675 - The tension of the string when the stone is
- at the bottom of the swing.
T =mw2r + mg
= 0.02 (62 x 0.5 + 10)
= 0.02 (28)
= 0.56 N - the top of the swing.
T= mw2r – mg
= 0.02 (62 x 0.5 – 10)
= 0.02 (8)
= 0.16 N - the linear velocity.
V = wr
= 6 x 0.5
= 3m/s
- at the bottom of the swing.
- The period T.
- -Radius of path
-
- Uniform acceleration is the constant change of velocity of a body per unit time.
-
- Maximum Height reached
distance covered in first 20seconds
s = ut + ½ at2
v=0
= ½ x 100 x (20) 2
= 20,000m
Distance covered after the first 20 seconds
v2 = u2 – 2as.
= v2-u2 = s
-2a
= 0-(2000)2
-2x10
= 200,000m
Hmax = 200,000+20,000
= 220,000m
=220 km - Total time taken = 20s + 200s = 220s.
- Newton’s second law of motion states that the rate of change of linear momentum is directly proportional to force and takes place in the direction of the force.
- M = 800kg
u = 25 m/s
f =?
V = 0
F = mv - mu
t
v2 = m2 – 2as
0 = (25)2 – 2 x a x 20
625 = - 40a
a = 15.625 m/s2
v = u – at
0= 25 – (-15.625)t
15.625t = 25 + 15.625
t = 25/15.625= 1.6s
F = mv – mu
t
= (800x0) – (800 x 25)
1.6
= -12,500N.
- Maximum Height reached
-
- Extra force was to overcome the weight of the body and friction
- Since V.R is 1, the worker pulls the ropes through 4 m
- Work = Force x distance
work = 200 x 4 = 800J
Deny ½ marks for missing units in F.A - Potential Energy
- Total Work = Effort x distance = 210 x 4 = 840 J
- η = Work output x 100
Work input
= 800 x 100 = 95%
840
-
-
- Measurements that should be taken in the experiment
-Length of column of dry air (½ mark)
-Temperature (½ mark)
-Length/ height of the mercury thread (½ mark)
-Volume of air (½ mark) - How the measurements taken are used to verify Charles’ Law
Temperature is varied and values of Length and Temperature are measured and recorded (½ mark); a graph of Length versus Temperature. is plotted (½ mark). This is a straight line cutting T axis at O (A) (½ mark) (or – 2730C) since tube is uniform Length α Temperature. (½ mark) - Determine the Volume
P1V1 = P2 V2 (½ mark) = 1.5.x 105 x 1.6 = 1.0 x 105 x V2 (½ mark)
T1 T2 285 273 - = V2 = 23m3 (1 mark)
- Measurements that should be taken in the experiment
-
- Time taken for all the ice to be just melted
Vit = mlf, 250 x 4 x t = 1 x 3.34 x 105,
t = 334 seconds or 5 minutes 34 seconds - Time taken until half the contents of the kettle get boiled away
Vit = mlf + mwcw∆θ + ½ mlv, (½ mark)
250 x 4 x t(½ mark) = 3.34 x 105 + 2 x 4200 x 100 + 1 x 2.26 x 106
t = 3434 seconds or 57 minutes and 14 second
- Time taken for all the ice to be just melted
-
Download PHYSICS PAPER 1 - 2019 KCSE STAREHE MOCK EXAMS (QUESTIONS AND ANSWERS).
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students