MATHEMATICS PAPER 2 - 2019 MOKASA II MOCK EXAMINATION

Instructions to Candidates

1. This paper consists of two sections: Section I and Section II.
2. Answer ALL questions from section I and ANY FIVE from section II
3. Show all the steps in your calculation, giving your answer at each stage
4. Non – Programmable silent electronic calculators and KNEC mathematical tables may be  used, except where stated otherwise.

SECTION I (50 MARKS)

Answer all the questions in this section

1. Use logarithm tables of trigonometry and numbers to evaluate;    (3 marks) 
   
2. By rounding each number to the nearest tens, approximate the value of, Hence, calculate the percentage error arising from this approximation to 4 significant figures.      (3 marks)
3. Determine the value of x for which the matrix below is singular.             (3 marks)
       
4. Simplify without using tables or a calculator (3marks)
      
5. Find the value of x in the equation in the range listed below.   (3marks)
6. Z is directly proportional to x² and inversely proportional to . If x is increased by 22.5% and y is decreased by 19.76%. Find the percentage change in Z.(3marks)
7. Triangle PQR has vertices P(-1, 2) Q(-1, 1) and R(1, -1). Find the matrix of transformation which maps triangle PQR onto triangle P¹ Q¹ R¹ whose vertices are P¹(-3, 2) Q¹(0, -1) R¹(2, -1). Describe the transformation fully. (3 marks)
8. The age distribution of 9 workers in a factory were: 32, 30, 28, 35, 33, 37, 33, 34, 32.Determine the semi-Interquartile range of the data.     (3 marks)
9. The first three terms of a geometric sequence are 2x, x-8 and 2x=5. Find the possible values of x.(3 marks)
10. 125 small white cubes are arranged to form one large cube. The sides of the large cube are then painted red, the cubes are then dismantled and one of the small cubes picked at random. Find the probability that the cube picked has two of its side painted red. (3 marks)                                                                                                           
11. The gradient function of a curve is given by theexpression 2x+1. If the curve passes through the point (-4,6).Find the equation of the normal to the curve at this point. (3marks)
12. Find the area enclosed by the curve y=81-x²and the x – axis using mid-ordinate rule with 9 strips. (4marks)
13. Two parallel chords of a circle are each 16cm long. If the radius of the circle is 10cm. Find the perpendicular distance between the chords. (3marks)
14. Line AB is the diameter of a circle such that the co-ordinates of its ends A and B are (-1, -4) and (7,2) respectively.
    1. Determine the centre and radius of the circle. (2marks)
    2. Hence find the equation of the circle. (1mark)

15. The table below shows income tax rates in Kenya.
    

    Monthly taxable income in Ksh	Tax rate percentage % in each shilling
    Upto 8680	10%
    From 8681 to 18900	15%
    From 18901 to 27920	20%

    During the year, Mong’are paid a net tax of Ksh. 5360 after a relief of Ksh. 1256 in a certain month. Calculate Mong’are’s net salary during the month if he enjoys a non-taxable travel allowance of Ksh. 5000.      (4marks)

16. Write down the expansion of,use the first three terms of the expansion to find out the value of correct to three decimal places.(3marks) 

SECTION II (50 MARKS)

Answer ANY FIVE questions in the spaces provided

17.  
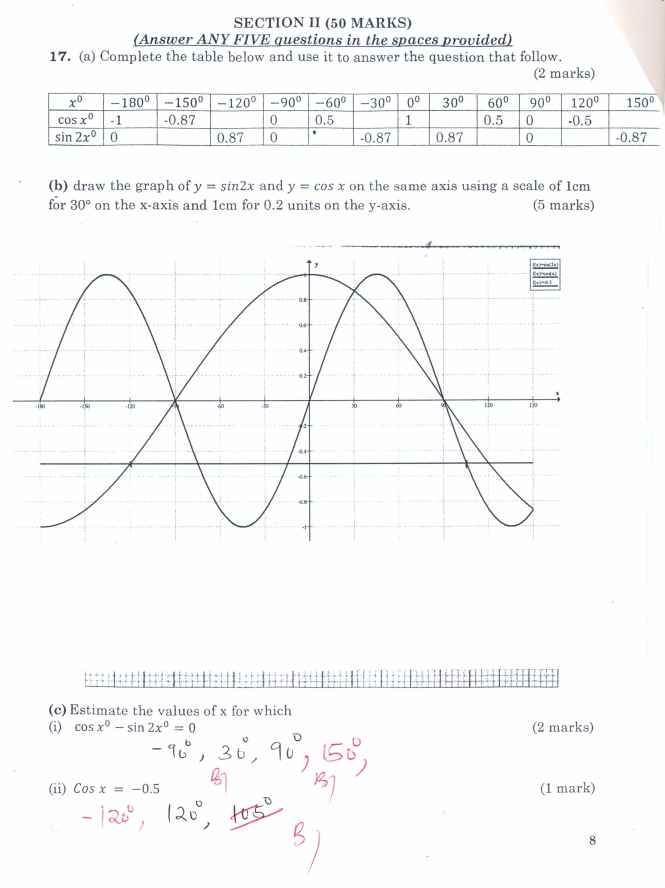
    1. Complete the table below and use it to answer the question that follow. (2marks)
       
    2. Draw the graph of  and y=cos x on the same axis using a scale of 1cm for 30⁰ on the x-axis and 1cm for 0.2 units on the y-axis.   (5 marks)
       
    3. Estimate the values of x for which
       1. cos x - sin 2x= 0 (2 marks)
       2. cos x = -0.5 (1 mark)

18. The diagram below represents a square based pyramid with equilateral triangles, AB = 8 cm.
    
    Calculate the:
    1. Height of the triangular faces. (2 marks)
    2. Length of AC (1 mark)
    3. Angle between VD and the base (3 marks)
    4. Angle between VAB and VBC (4 marks)
19.  
    1. A farmer bought a tractor at Ksh.1800000. The tractor’s depreciation rate is 12% p.a. Find the number of full years it willtake for the value of the tractor to depreciate to Ksh. 800000. (3marks)
    2. At the start of the eighth year, the tractor was sold at a value that is Ksh. 200,000 more than its actualvalue. If the selling price was to be taken as its actual value at the start of the eight year, find the tractors semi annual rate of depreciation.(4marks)
    3. The hire purchase of a table is Ksh. 16800. If 25% is paid as deposit and the rest of the money is spread over 10 equal monthly installments. Find the amount of each installment. (3marks)

20. The diagram represents parts of a curve y = 2x - x²
    
    Calculate:
    1. the coordinates of A (2 marks)
    2. the area bounded by curve and the x-axis. (3 marks)
    3. The equation of the curve is y= 2x³-5x²-x Calculate the angle between the x- axis and tangent to the curve at (2, -6) (5 marks)  

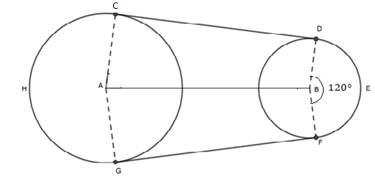
21. The diagram represents two pulley wheels, centres A and B with a rubber band CDEFGHC stretched round them. Radius of the wheel centre A is 12cm, AB = 20cm, CD, GF are tangents to the circles. Angle DBF = 120⁰.
    
    Calculate
    1. Length
       1. BD (2 marks)
       2. CD (2 marks)
    2. Arc lengths;
       1. CHG (2marks)
       2. DEF     (2marks)
    3. The total length of the belt (2marks)

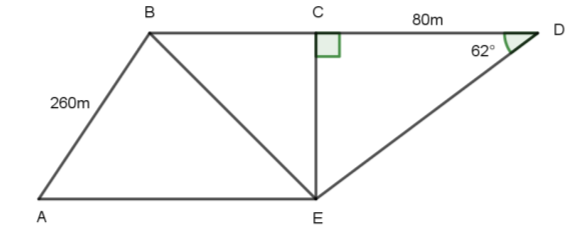
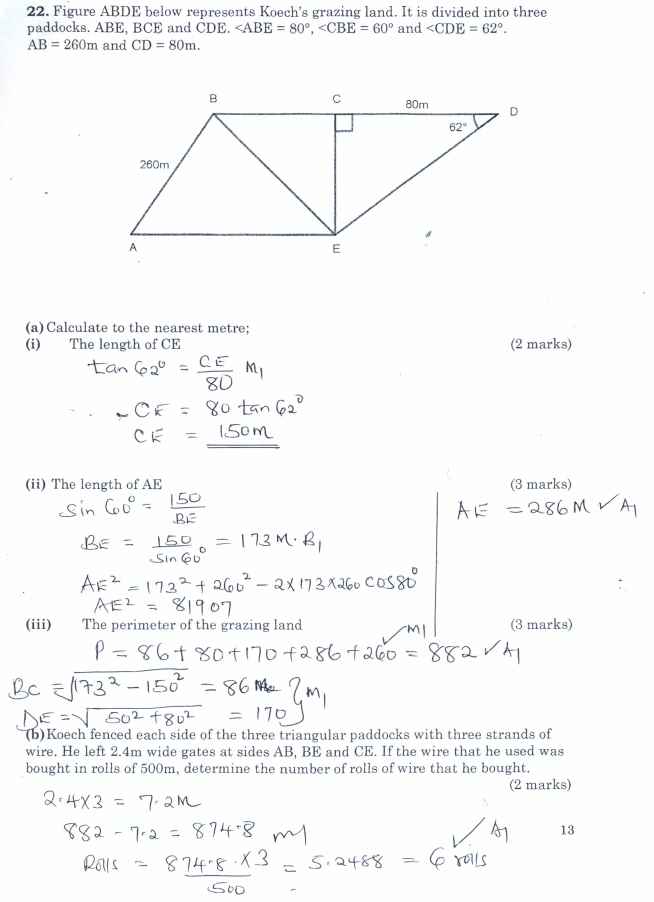
22. Figure ABDE below represents Koech’s grazing land. It is divided into three paddocks. ABE, BCE and CDE. ˂ABE = 80°, ˂CBE = 60° and ˂CDE = 62°. AB = 260m and CD = 80m.
    
    1. Calculate to the nearest metre
    2. The length of CE (2 marks)
    3. The length of AE (3 marks)
    4. The perimeter of the grazing land (3 marks)
    5. Koech fenced each side of the three triangular paddocks with three strands of wire.He left 2.4m wide gates at sides AB, BE and CE. If the wire that he used was bought in rolls of 500m, determine the number of rolls of wire that he bought. (2 marks)
23. Construct the triangle ABC in which AB = 5cm, angle BAC = 60° and angle ABC = 90°. Measure the length BC (1 mark)
    1. Construct the circumcircle of triangle ABC (2 marks)
    2. On the same side of AB as C, construct the locus of point P such that the area of triangle ABP is half the area of triangle ABC.       (4 marks) 
    3. Mark and label clearly a point Q such that AQB is 30°.         (3marks)
24. P and Q are two points on a geographical globe of diameter 50 cm. They both lie on a parallel latitude 50^o P has longitude 90^o West and Q has longitude 90^o East. A string AB has oneend at point P and another at point Q when it is stretched over the North pole. Taking π = 3.142;
    1. Calculate the length of the string. (3 marks)   
    2. If instead the string is laid along the parallel of latitude 50^oN with A at point P, calculate the longitude of point (3 marks)     
    3. State the position of B if the string is stretched along a great circle of P towards the South pole if point A is static at P. (4 marks)         

MARKING SCHEME