INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections: Section I and Section II.
- Answer ALL questions from section I and ANY FIVE from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise
SECTION A (50 marks)
Answer all questions in this section
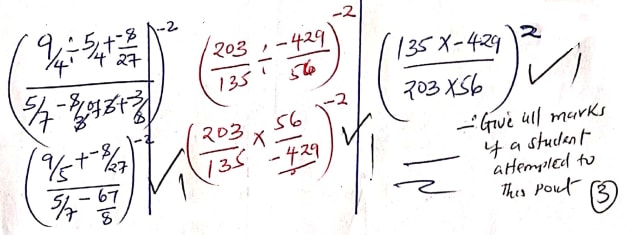
- Without using a calculator or tables, evaluate: (3 marks)
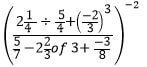
- Solve the equation for x. 5(2x+1)+52x − 750 = 0 (3 marks)
- Simplify (3 marks)
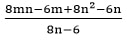
- Use squares, square roots and reciprocals tables to evaluate the following giving your answer to 2 decimal places. (4 marks)
1 + 2
√20.52 (6.23)2 - Susan made a loss of 20% by selling a blender at sh. 2,400. What profit would she have made had she sold it at sh. 3300? (3 marks)
- Solve for x and y using substitution method:
1/3(x + y) – 2 = 0
1/4(x − y) = 1 (3 marks) - The number of sides of two regular polygons differs by one. If the sum of the interior angles of these polygons is in the ratio 2:3, calculate the number of sides of each polygon and name them. (3 marks)
- Solve for x in the following equation: Sin(1/2x − 10°) = Cos2x (3 marks)
- A vehicle moves at an initial speed of 20 m/s with a constant acceleration of 2 m/s2 for five seconds before breaks are applied. If the car comes to rest under constant deceleration 4 seconds, determine the total distance travelled during the 9 seconds (3 marks)
- Simplify completely the expression (4 marks)
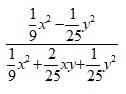
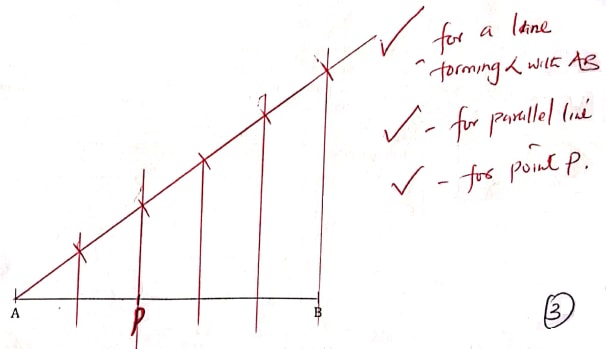
- A point P divides the line AB shown below internally in the ratio 2:3. By construction, find the position P and measure AB. (3 marks)

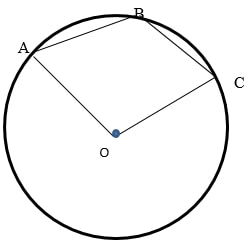
- In the figure below, O is the centre of the circle and reflects angle AOC = 142°. Find angle ABC. (3 marks)
- A tourist arrived in Kenya with 10,000 US dollars which he converted to Ksh on arrival. He spent Kshs.428,500 and converted the remaining amount to Sterling pounds. How much did he receive in Sterling pounds? The currency exchange rate of the day was as follows; (3 marks)
Currency
Buying
Selling
1 Sterling pound
135.50
135.97
1US dollar
72.23
72.65
- Adam harvested 200 bags of wheat from 2 ha of his farm. How many bags of wheat would he harvest from 16 ha if he maintained the rate? (3 marks)
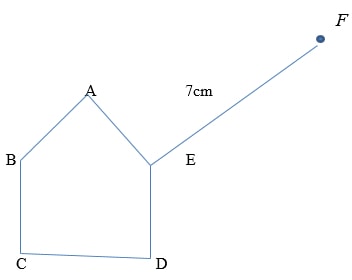
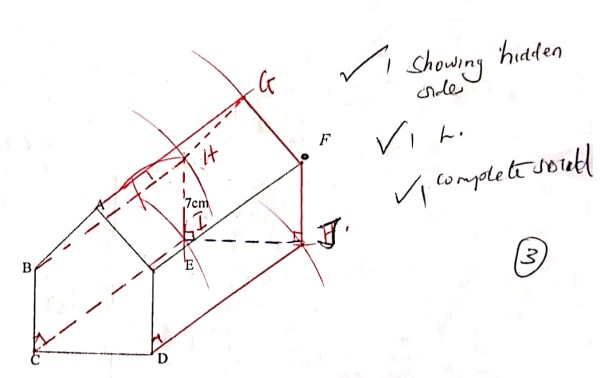
- Complete the solid below whose length is 7cm (3 marks)
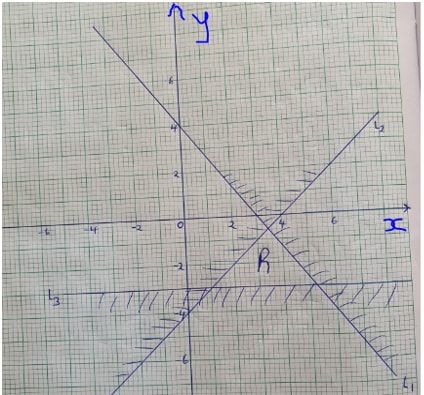
- Write down three inequalities which fully describe the unshaded region R in the figure below (3 marks)
SECTION B (50 marks)
Answer any five questions from this section
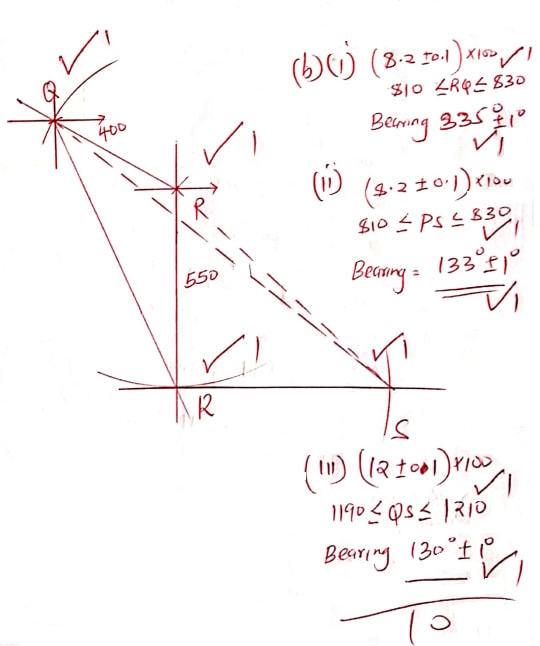
- Three points P, Q and S are pm the vertices of a triangular plain field. P is 400m from Q on a bearing of 3000 and R of 550m directly south of P.
- Using a scale of 1 cm to represent 100m on the ground, draw a diagram to show the position of the points. (3 marks)
- Use the scale drawing to determine;
- The distance and bearing of Q from R. (2 marks)
- The bearing and distance of point S from P given that point S is directly 600m East of R. (3 marks)
- The bearing and distance of Q from S. (2 marks)
- A bus travelling at a speed of 80km/hr left Mombasa at 8.00am for Nairobi. Two hours later, a car travelling at a speed of 100km/hr left Nairobi for Mombasa.
- Given that the distance between both cities is 500km, find the time of the day when the two vehicles met. (6 marks)
- After meeting, the speed of both vehicles dropped to 60km/hr due to traffic jam. At what time did each vehicle arrive at its destination? (4 marks)
- The figure below represents an histogram of heights against age brackets of members of a village.
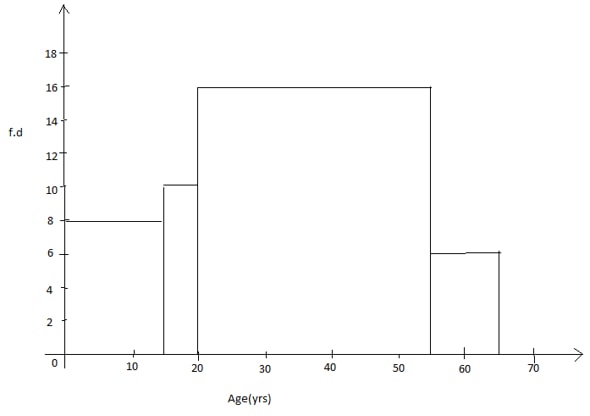
Using the figure above,- Develop a frequency distribution table (3marks)
- Using the table in (a) above find;
- The mean. (3marks)
- The median class (1mark)
- The median (3marks)
- The diagram below shows a container base made of a frustum of a square pyramid. The top is a solid frustum of a cone.
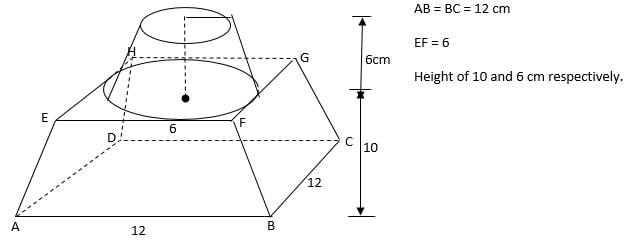
- Calculate the surface area of the bottom solid. (5 marks)
- Calculate the surface area of the top side. (4 marks)
- Calculate the total area. (1 mark)
-
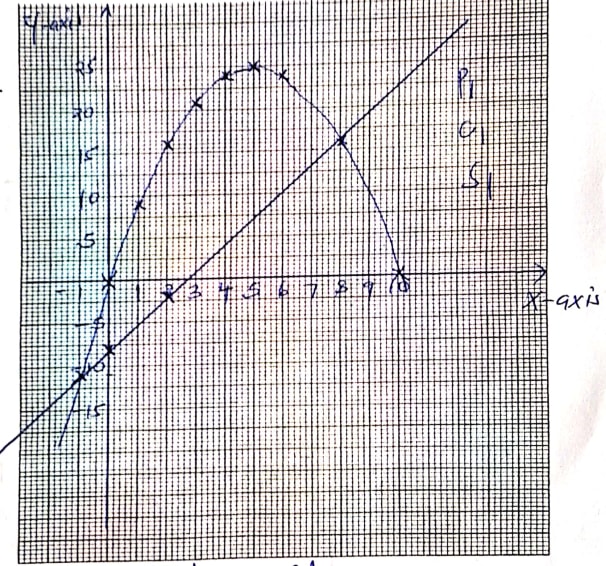
- Complete the table below for the function
y = −x2 + 10x (2marks)
X −1 0 1 2 3 4 5 6 8 10 Y 9 24 0 - On the grid provided draw the graph of y=-x2 + 10x (3marks)

- Using the graph above solves the equations:
- 10x − x2 = 0 (2marks)
- x2 − 7x − 8 = 0 (3marks)
- Complete the table below for the function
- Two lines L1 = 2y − 3x − 6 and L2=3y+x-20=0 intersect at point A.
- Find the coordinates of A (3marks)
- A third line L3 is perpendicular to L2 at point A. Find the equation of L3 in form of y=mx+c, where m and c are constants. (3marks)
- Another line L4 is parallel to L1 and passes through (−1,3). Find the x-intercept and the y-intercept of L4. (4marks)
-
- PQRS is a quadrilateral with vertices P(1,4), Q(2,1), R(2,3) and S(6,4). On the grid provided, plot the quadrilateral. (1 mark)

- Draw P’Q’R’S’ the image of PQRS under a positive quarter turn about the origin and write down its co-ordinates. (3 marks)
- Draw P”Q”R”S” the image of P’Q’R’S’ under an enlargement scale factor -1 and center (0,0) and write down its co-ordinates. (3 marks)
- Determine the matrix of a single transformation that maps PQRS onto P”Q”R”S (3 marks)
- PQRS is a quadrilateral with vertices P(1,4), Q(2,1), R(2,3) and S(6,4). On the grid provided, plot the quadrilateral. (1 mark)
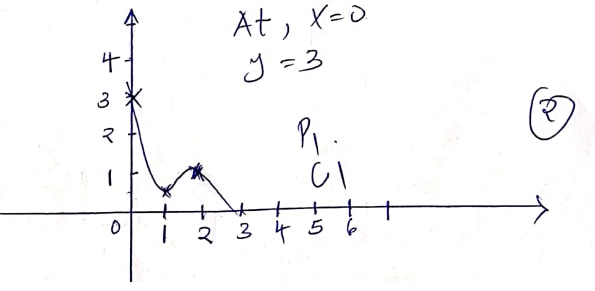
- A curve whose equation is 3y = 9 − 18x + 27/2x2 − 3x3 turns at points P and R.
- Find the coordinates of P and R (5 marks)
- Determine the nature of points P and R (3 marks)
- Sketch the curve (2 marks)

Marking Scheme
-
- 52x+1 + 52x = 750
52x.51 + 52x = 750
52x(5+1) = 750
52x(6) = 750
52x = 125
52x = 53
2x = 3
x = 1.5 - 2m(4n − 3) + 2n(4n−3) = (4n − 3)(2m + 2n)
2(4n − 3) 2(4n − 3)
= 2(m + n)
2
= m+n - √20.56 = 4.5299
(6.23)2 = 38.81
1(Reciprocal 4.530) + 2 (Reciprocal 38.81)
0.2208 + 2 × 0.02576
= 0.2208 + 0.05152
= 0.27232 - 80% = 2400
100% = ?
100 × 2400
80
= 3,000
3300 − 3000
= 300 - x + y − 6 = 0
x − y − 4 = 0
x = y + 4
(y + 4) + y = 6
2y = 2
y = 1
x = 1 + 4
= 5 - 180 (n − 2) = 2
180 (n + 1 −2) 3
3 (n−2) = 2(n−1)
3n − 6 = 2n − 2
3n − 2n = 6 − 2
n = 4 - Quadrilateral
n + 1 = 5 - Pentagon - (1/2x − 10) + 2x = 90
2.5x = 100
x = 40 -
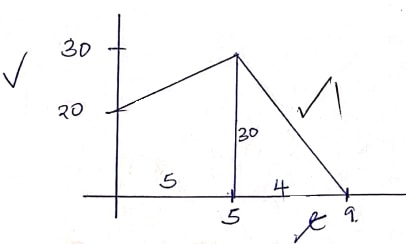
v − u = a
t
v − 20 = 2
5
v − 20 = 10
v = 30
D = (30 + 20)5 + 1/2 × 30 × 4
2
= 125 + 60
= 185 m -
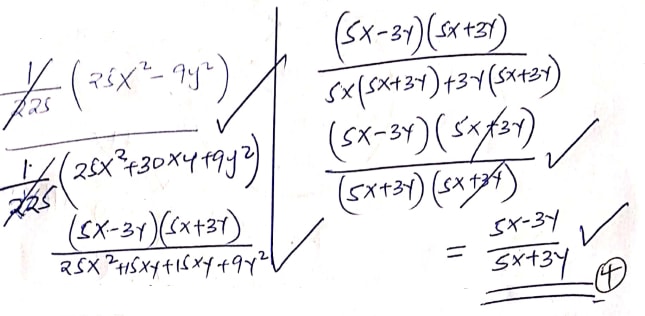
-
-
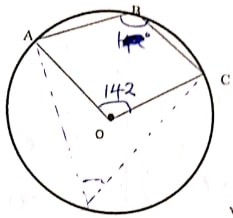
∠ABC = 180° − 1/2(142)
= 180° − 71
= 109°
Alt ∠ ABC = 360 − 142
2
= 218/2
= 109° - 1 US dollar = 72.23
(10000 × 72.23)
Sh. 722300
Spend 428500
(Sh. 722300 − 428500)
= Sh. 293, 800
1 sterling pound = sh. 135.97
? = sh. 293, 800
293, 800 = 2160.8 sterling pounds
135.97 - Bags Farm
200 2ha
? 16ha
16/2 × 200
= 1600 bags -
-
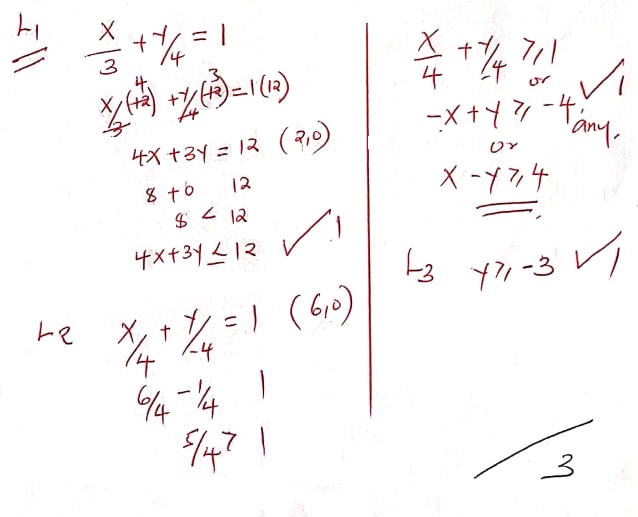
-
-
-
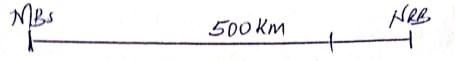
D = T × S
= 2 × 80
= 160 km
500 − 160 = 340 km
A.S = 80 + 100
= 180 km/h
T = D/S
T = 340/180
= 17/9
= 1 8/9 hrs → 1 hr 53mins 20 secs
10:00:00
+1:53:20
11: 53:20 a.m - D = T × S
= 17/9× 100
Distance covered at the time of meeeting
18/9 × 80 = 151 1/9 Km
Bus = 160 + 151 1/9 = 311 1/9 Km
Car = 151 1/9 Km
Remaining distance
Bus = 500 − 311 1/9 Km = 188 8/9 Km
Car = 500 − 151 1/9 Km = 348 8/9 Km
Time taken by
Bus = 188 8/9 ÷ 60
= 3 hr 9 mins
Car = 348 8/9 ÷ 60 = 5 hrs 49 min
Arrival time
Bus 11:53
3:09
1502 hrs
Car 1153
549
1742hrs
-
-
-
x f x xf cf 0 - 15 120 7.5 900 120 15 - 20 50 17.5 875 170 20 - 55 560 47.5 26600 730 55 - 65 60 60 3600 790 850 31975 -
- x̄ = 31975/790
= 40.475 - 790/2 = 395th
20 - 55 - 20 + (395 − 170)35
730
= 30.788
- x̄ = 31975/790
-
-

-
-
X −1 0 1 2 3 4 5 6 8 10 Y −11 0 9 16 21 24 25 24 16 0 -
-
- x = 0 or x = 10
- y = − x2 + 10x + 0
0 = x2 − 7x − 8
y = 3x − 8
x = 0, y = −8, (0, −8)
x = 2, y = −2 (2, −2)
x= -1 or x = 8
-
-
- (2y − 3x = 6)3
(3y + x = 20)2
6y − 9x = 18
6y + 2x = 40
−11x = −22
x = 2
2y − 3(2) = 6
2y = 12
y = 6
A(2,6) - 3y = −x + 20
y = −1/3x + 20/3
m = 3
y − 6 = 3
x − 2 1
y − 6 = 3x − 6
y = 3x + 0 - 2y = 3x + 6
y = 3/2x + 3
y − 3 = 3
x + 1 2
2(y−3) = 3 (x + 1)
2y − 6 = 3x + 3
2y = 3x + 9
y = 3/2x + 9/2
x - intercept y = 0
2/3 × 3/2x = −9/2 × 2/3
x = − 3
y - intercept x = 0
y = 9/2
y = 4.5
- (2y − 3x = 6)3
-
-
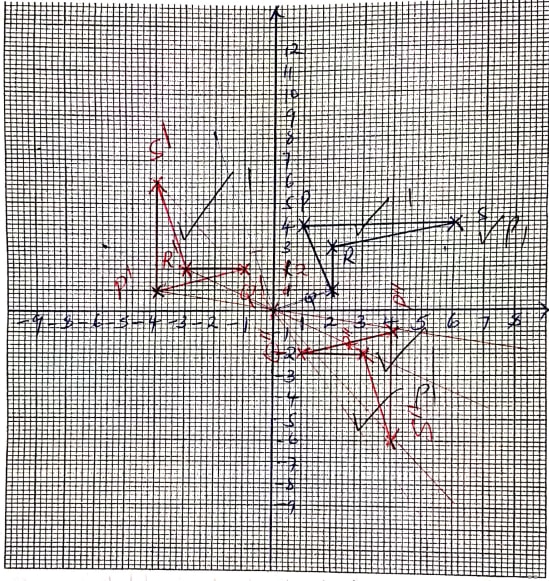
- P' (−4, 1) Q'(−1,2) R'(−3,2) S'(−4,6)
- P" (4, −1) Q"(1, −2) R"(3, −2) S"(4, −2)
- The transformation of +90° about the origin
✓1 for constructions
-
-
- [3y = 9 − 18 x + 27/2x2 − 3x3]1/3
y = 3 − 6x + 4.5x2 − x3
dy/dx = − 6 + 9x − 3x2
at s.t.p dy/dx = 0
−6 + 9x − 3x2 = 0
x2 − 3x + 2 = 0
x(x−1) − 2(x−1) = 0
x = 1 or x = 2
when x = 1, y = 3 − 6 + 4.5 + 1
y = 1/2
when x =2, y = 3 − 12 + 18 − 8
y = 1
P1 (1, 1/2) P2 (2,1) - y" = 9 − 6x
at x = 1
y = 9 − 6 = 3
P1 (1, 1/2) min point
y" = 9 − 6x at x = 2
y" = 9 − 6(2) = − 3
P2 (2,1) max point -
- [3y = 9 − 18 x + 27/2x2 − 3x3]1/3
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Kassu Jet Joint Exams 2020/2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

