Physics Paper 3 Questions and Answers - Moi Kabarak High School Mock 2020/2021

Instructions to candidates

• Answer all the questions.
• You are supposed to spend the first 15 minutes of the 2-3 hours allowed for this paper reading the whole paper carefully before commencing your work.
• Marks are given for a clear record of the observations actually made, their suitability, accuracy and the use made of them.
• Candidates are advised to record their observations as soon as they are made.
• Non-programmable silent electronic calculators may be used. 
• Candidates should answer the questions in English.

PART A

Question 1
You are provided with the following:

• Some water in a container
• A 10ml measuring cylinder
• A piece of a glass rod
• A 10g mass
• 5 paper clips
• A half metre rule
• A metre rule
• Two stands, two bosscs and two clatips
• Three pieces of sewing thread
  
  Proceed as follows:
  
  
  1. Pour 6ml of the water into the measuring cylinder. Lower the glass nod into the water and detemine the volume V of the glass rod.
     V=.......... cm³             (½mark)
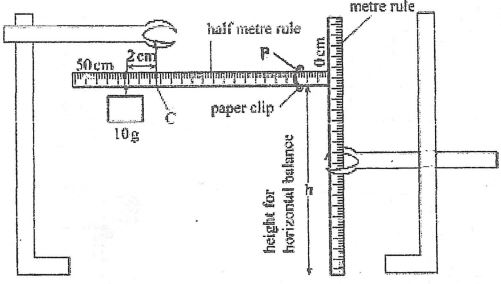
     Remove the glass rod from water
  2. Using a stand and a piece of string, suspend the half metre rule at its centre of gravity C so that it balances horizontally with the scale facing you.
     Using a second stand, clamp a metre rule vertically near one end of the half metre rule to note the height at which the half metre rule is horizontal.
     Maintain this height throughout the experiment
     Record the centimetre mark of the centre of gravity C.         
     C=------------ cm             (1 mark)
  3. Using the string, suspend the 10g mass on the half metre rule at a distance d = 2 cm from C. The distance d = 2cm should be maintained throughout the experiment.
     Balance the half metre rule by suspending the glass rod using a string at a distance X from C
     Record the value of X
     X...........cm         (½ mark)
  4. Using the results in part(a) and (c) determine the density of the glass rod.     (3 marks)
  5. Remove the glass rod. Push the half metre rule through one paper clip and adjust the position of the clip to a point P where the half metre rule balances horizontally. See Figure 1..
     
                              Figure 1
  6. Record the centimete mark for point P in Table 1.
  7. Repeat part (f) for the other number of clips shown in Table 1 and complete (the clips may be suspended by connecting them as a chain of the required nnumber)       (4 marks)
                              Table 1
     

     Number of clips N	1	2	3	4	5	6
     cm mark of P(cm)
     distance L (from c to p)
     1/L (cm−1)

  8. Plot a graph ¹/_L (y axis) against the number of clips N      (4 marks)
  9. Determine the slope S of the graph.    (2 marks)
  10. Determinine K given that: ¹/_L = 0.05 KN          (2 marks)
      
      PART B
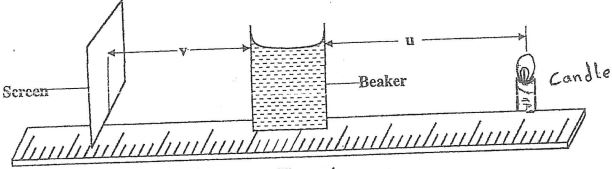
      Proceed as follows:
  11. Place the 100 ml beaker on a meter rule and pour 80 cm³ of water into it. Arrange the candle and screen on either side of the beaker. (see figure 4)
      
  12. Adjust the position of the candle on the metre rule so that its centre is a distance u = 12 cm from the beaker. Light the candle & adjust the position of the screen until a well focused image of the candle is formed on the screen. Measure and record in table 1 the image distance V between the screen and the beaker.
  13. Repeat part (1) for other values of u shown in table 1 and complete the table.
                     Table 1
      

      Distance u (cm)	12	16	20
      Distance v (cm)
      y=  uv        u+v

                                                       (3 marks)
  14. Determine m, the mean value of y using the values in table 1.            (1 mark)
      m=.......
  15.  
      1. With the meter rule outside the beaker, measure the height h of the water meniscus above the bench.               (1 mark)
         h = ........ cm
      2. Determine the value of P given that           (1 mark)
         P=⁵/_√h
      3. Hence determine the value of f given that f =^p/_2m + 1 to one decimal place.     (2 marks)

Question 2

You are provided with the following:

• an ammeter
• a voltmeter
• two cells (size D)
• a cell holder
• a switch
• a wire labelled L mounted on a millimetre scale
• a micrometer screw gauge (to be shared)
• six connecting wires at least four with crocodile clips
  
  Proceed as follows:
  
  
  1. Using a micrometer screw gauge, measure and record the diameter d of the wire L.     (1 mark)
     d= ............................... mm
     d = ............... m.
  2. Place the two cells in series in the cell holder and use the voltmeter to measure the total electromotive force (emf) E₀ of the battery.                   (1 mark)
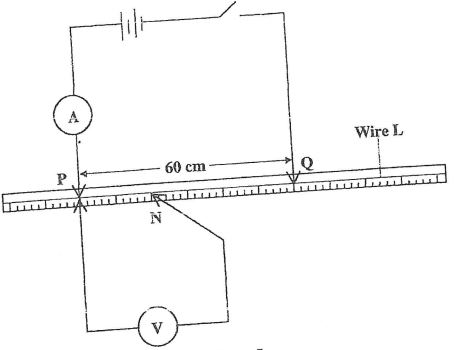
     E₀= ........ V.
  3. Starting with the switch open, connect the circuit as shown in Figure 5. P and Q are points on the wire L such that PQ is 60 cm. (PQ should remain 60 сm throughout the experiment) N is a point on the wire such that PN is 10 cm (0.1 m).
     
  4.  
     1. Close the switch and record the current I.           (1 mark)
        I = ....................... A.
     2. Measure and record in table 2 the potential difference across PN.
     3. Measure and record the potential difference across PN for the other values of PN shown in table 2 and complete the table. (The current is expected to remain constant) Hint: The switch should be closed only when reading the voltmeter.
                                      Table 2
        

        Length PN (m)	0.1	0.2	0.3	0.4	0.5	0.6
        P.d (V)
        Resistance v/I (Ω)

        (6 marks)
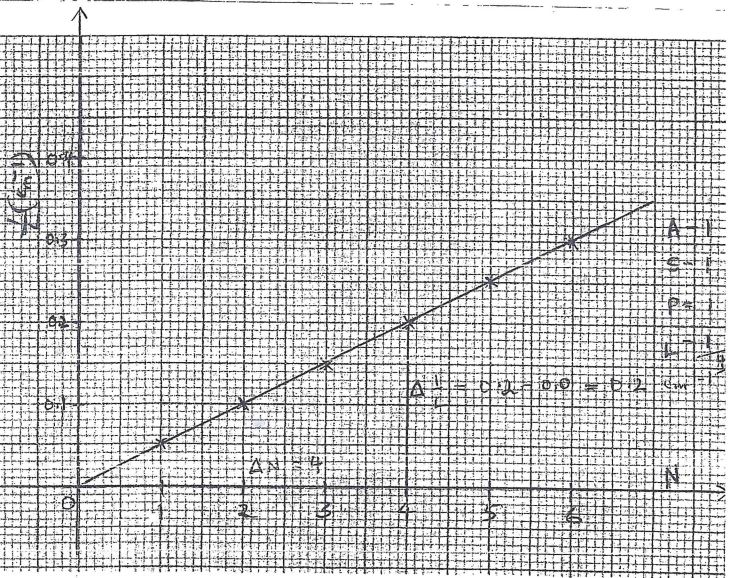
  5. On the grid provided,plot a graph of resistance (y-axis) against length.         (3 marks)
  6. From the graph, determine:
     1. the slope S and its units.               (3 marks)
     2. the constant k and its units given that           (3 marks)
          S=  4k 
                πd²
  7. Determine constant t given that
     
     where V_n is the p.d at PN =0.6 m.             (2 marks)

Marking Scheme

PART A

Question 1
You are provided with the following:

• Some water in a container
• A 10ml measuring cylinder
• A piece of a glass rod
• A 10g mass
• 5 paper clips
• A half metre rule
• A metre rule
• Two stands, two bosscs and two clatips
• Three pieces of sewing thread

  Proceed as follows:

  1. Pour 6ml of the water into the measuring cylinder. Lower the glass nod into the water and detemine the volume V of the glass rod.
     V=  3.5 ± 0.5 cm³             (½mark)
     Remove the glass rod from water
  2. Using a stand and a piece of string, suspend the half metre rule at its centre of gravity C so that it balances horizontally with the scale facing you.
     Using a second stand, clamp a metre rule vertically near one end of the half metre rule to note the height at which the half metre rule is horizontal.
     Maintain this height throughout the experiment
     Record the centimetre mark of the centre of gravity C.         
     C =  25.0 ± 0.3 cm             (1 mark)
  3. Using the string, suspend the 10g mass on the half metre rule at a distance d = 2 cm from C. The distance d = 2cm should be maintained throughout the experiment.
     Balance the half metre rule by suspending the glass rod using a string at a distance X from C
     Record the value of X
     X = 2.2 ± 1.0 cm         (½ mark)
  4. Using the results in part(a) and (c) determine the density of the glass rod.     (3 marks)
     Mass = 2 × 10 = 9.091g
                   2.2
     density = 9.091 =2.597 g/cm³
                     3.5
  5. Remove the glass rod. Push the half metre rule through one paper clip and adjust the position of the clip to a point P where the half metre rule balances horizontally. See Figure 1..
     
                              Figure 1
  6. Record the centimete mark for point P in Table 1.
  7. Repeat part (f) for the other number of clips shown in Table 1 and complete (the clips may be suspended by connecting them as a chain of the required nnumber)       (4 marks)
                              Table 1
     

     Number of clips N	1	2	3	4	5	6
     cm mark of P(cm)  ± 2.0	5.0	15.0	18.3	20.0	21.0	21.7
     distance L (from c to p)	20.0	10.0	6.7	5.0	4.0	3.3
     1/L (cm−1)	0.05	0.10	0.1493	0.20	0.25	0.3030

  8. Plot a graph ¹/_L (y axis) against the number of clips N      (4 marks)
     
  9. Determine the slope S of the graph.    (2 marks)
     Slope S =0.2 − 0 = 0.2 =0.05cm⁻¹
                       4−0         4
  10. Determinine K given that: ¹/_L = 0.05 KN          (2 marks)
      0.05K = 0.05
             K = 0.05 = 1
                    0.05
      PART B

      Proceed as follows:

  11. Place the 100 ml beaker on a meter rule and pour 80 cm³ of water into it. Arrange the candle and screen on either side of the beaker. (see figure 4)
      
  12. Adjust the position of the candle on the metre rule so that its centre is a distance u = 12 cm from the beaker. Light the candle & adjust the position of the screen until a well focused image of the candle is formed on the screen. Measure and record in table 1 the image distance V between the screen and the beaker.
  13. Repeat part (1) for other values of u shown in table 1 and complete the table.
                     Table 1
      

      Distance u (cm)	12	16	20
      Distance v (cm)  ±1.0	5.0	4.5	4.0
      y=  uv        u+v	3.529	3.512	3.333

                                                       (3 marks)
  14. Determine m, the mean value of y using the values in table 1.            (1 mark)
      m= 3.528+3.512+3.333
                        3
         =10.374
                3
         =3.458cm
  15.  
      1. With the meter rule outside the beaker, measure the height h of the water meniscus above the bench.               (1 mark)
         h = 4.1 cm
      2. Determine the value of P given that           (1 mark)
         P=⁵/_√h
           = ⁵/_2.018 = 2.477
      3. Hence determine the value of f given that f =^p/_2m + 1 to one decimal place.     (2 marks)
         f=     2.477   +1
              2 × 3.458
          =0.3582 + 1
          =1.3582
         =1.4

Question 2

You are provided with the following:

• an ammeter
• a voltmeter
• two cells (size D)
• a cell holder
• a switch
• a wire labelled L mounted on a millimetre scale
• a micrometer screw gauge (to be shared)
• six connecting wires at least four with crocodile clips

  Proceed as follows:

  1. Using a micrometer screw gauge, measure and record the diameter d of the wire L.     (1 mark)
     d= 0.30 ± 0.03 mm
     d = 0.00030 or 3.0× 10⁻⁴ m.
  2. Place the two cells in series in the cell holder and use the voltmeter to measure the total electromotive force (emf) E₀ of the battery.                   (1 mark)
     E₀= 3.00V. (2d.p) his value
  3. Starting with the switch open, connect the circuit as shown in Figure 5. P and Q are points on the wire L such that PQ is 60 cm. (PQ should remain 60 сm throughout the experiment) N is a point on the wire such that PN is 10 cm (0.1 m).
     
  4.  
     1. Close the switch and record the current I.           (1 mark)
        I = 0.14A. (2d.p)  his value
     2. Measure and record in table 2 the potential difference across PN.
     3. Measure and record the potential difference across PN for the other values of PN shown in table 2 and complete the table. (The current is expected to remain constant) Hint: The switch should be closed only when reading the voltmeter.
                                      Table 2  Increasing trend
        

        Length PN (m)	0.1	0.2	0.3	0.4	0.5	0.6
        P.d (V)	0.22	0.42	0.60	0.80	1.00	1.25
        Resistance v/I (Ω)	1.5714	3.00	4.2857	5.714	7.1429	9.2857

        (6 marks)
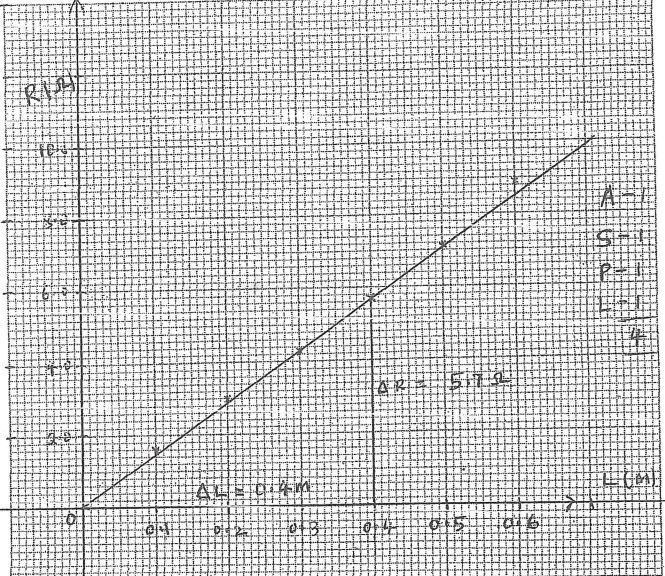
  5. On the grid provided,plot a graph of resistance (y-axis) against length.         (3 marks)
     
  6. From the graph, determine:
     1. the slope S and its units.               (3 marks)
        Slope S =^5.7/_0.4 =14.25 Ωm⁻¹
     2. the constant k and its units given that           (3 marks)
          S=  4k 
                πd²
        K= Sπd² =14.25 × 3.142 × (3.0 × 10⁻⁴)²
                4                          4
          =1.0074 × 10⁻⁶ Ωm
  7. Determine constant t given that
                  E_o =3.0V
     where V_n is the p.d at PN =0.6 m.             (2 marks)
     V_n = 0.14 × 8.5 =1.19V   his value from table or graph
      t = 3.00 − 1.19  = 1.81  = 12.9286Ω
                 0.14            0.14