Instructions to candidates
- Write your name and index number in the spaces provided above.
- Sign and write the date of the examination in the spaces provided above.
- The paper contains TWO Sections: Section I and Section II.
- Answer ALL the questions in Section I and only five questions from Section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise,
- This paper consists of 16 printed pages.
- Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.
FOR EXAMINER'S USE ONLY
SECTION I
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Total |
SECTION II
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | TOTAL |

QUESTIONS
SECTION 1: (50 Marks)
Answer all questions in this section in spaces provided
1. Evaluate: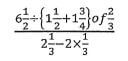 (3 marks)
(3 marks)
2. Solve for n 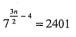 (3 marks)
(3 marks)
3. Simplify the expression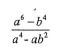 (3 marks)
(3 marks)
4. The figure shows an equilateral triangular prism ABCDEF of side 4em and length 10cm, H and G
are the midpoints of side FB and DE. On the surface of the prism is a continuous path AGCH. Draw and label anet of the prism and on the same net show the path.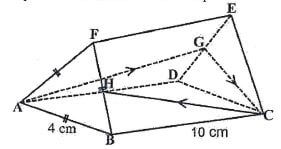 (3 marks)
(3 marks)
5.The GCD and LCM of three numbers are 24 and 5040 respectively. If two of the numbers are 48 and 72, find the least possible value of the third number.
(3 marks)
6. The position vectors of A and B are, a = 4i + 3j and b = 8i-j.
- Find the column vector AB (1 mark)
- Hence find the length of AB leaving your answer in simple surd form (2 marks)
7. Use matrix method to solve the following simultaneous equations (3 marks)
3y + 2x = 5
x - 5y9
8. A solid made by mounting a conical frustum on hemisphere is illustrated below.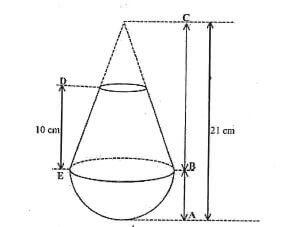
Given that AC=21 cm, AB
AC and DE = 10 cm, calculate the volume of the solid in terms of TT (4 marks)
9. Using a ruler and a pair of compasses only, construct triangle ABC in which AB - 6cm BC=Scm and angle ABC - 135o. Construct a perpendicular line from C to meet AB produced at point T. (3 marks)
10. A forex bureau in Nairobi Kenya, buys and sells foreign currencies at the rates shown below.
| Buying Ksh. | Selling Ksh. | |
| 1 Euro | 129.80 | 131.60 |
| 1 UAE Dirhams | 28.40 | 29.80 |
A Belgian tourist arrived in Nairobi, Kenya with 5000 Euros. She converted the whole amount to the local currency. While in Kenya she spent Ksh.321200 and changed the balance to UAE Dirhams before leaving for Dubai. Calculate the amount, in UAE Dirhams that she received.(3 marks)
11. The diagram below shows a velocity time graph for a journey. The total distance travelled is 1375m.Calculate the maximum speed attained in km/h. (3 marks)
(3 marks)
vms)
12. A particle moves in a straight line such that its displacement s meters per second is given by
s=t3-5t2 + 3t +3
Find the values of the time t, when the particle is momentarily at rest. (3 marks)
13. Without using tables or a calculator, evaluate 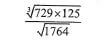 (3 marks)
(3 marks)
14. Solve for x in the equation 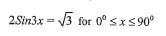 (3 marks)
(3 marks)
15. Use logarithms correct to 4 decimal places to evaluate (4 marks)
(4 marks)
16. The diagram below shows part of figure with a rotational symmetry of order 4 about point o.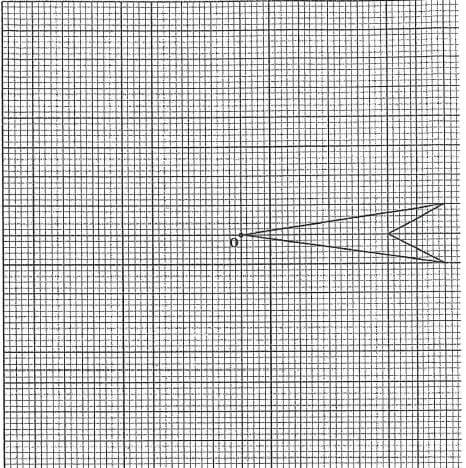
- Complete the diagram. (2 marks)
- Draw all the lines of symmetry of the figure drawn. (1 mark)
SECTION II: (50 Marks)
Answer only five Questions in this section in spaces provided
17. The parents of Umoja secondary school decided to buy a lab equipments worth Ksh. 900,000. Each
student was to contribute the same amount of money. Before they made the contribution 50 students transferred from the school, as a result, each of the remaining students had to pay Ksh. 600 more
- Taking x to represent the original number of students, write down an expression for:
- The original contribution per student (1 mark)
- The new contribution per student (1 mark)
- Find the original number of the students in the school (4 marks)
- Find the percentage change in contributions per student (2 marks)
- If the ratio of boys to girl that remained in the school was 11: 7 find the amount money contributed by boys. (2 marks)
18.
- A line L1 has the x and y intercepts at -2 and 4 respectively, find the equation of L1 in the form ax+by = c where a, b and care integers (2 marks)
- Another line L2 is perpendicular to L1 and cuts the x-axis at x = 3. Find the equation of L2 in the form y=mx+c (4 marks)
- Determine the point of intersection of L1 and L2 (4 marks)
19. Four stations P,Q,R and S are such that station Q is 160km on a bearing of 080º from station P. Station R is 240km due north of station Q, station S is on a bearing of 300º from P and on a bearing of 240° from R.
- Using a scale 1 cm represents 40km, show the relative positions of the four stations. (4 marks)
- Using the scale diagram in (a) above determine;
- Distance and bearing of S from Q. (2 marks)
- Distance SR (1 mark)
- Area of the region PQRS in square kilometers correct to 2 decimal places (2 marks)
20. In the diagram below, AD is parallel to EP, triangle ABC is right angled at point B. The area of △ABC is equal to area of △BED.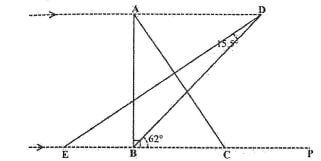
- Given that EB=5 cm, AC=13 cm, BD=12 cm, ∠CBD=62° and ∠BDE = 15.5° Calculate correct to 4.s.f the length of:
- AB (1 mark)
- DC,(3 marks)
- ED,(3 marks)
- If a circle is drawn passing through the vertices BED, calculate the area of the circle.,(3 marks)
21. In an Agricultural Research Institute, the length of a sample of 50 maize cobs were measured and recorded as shown in the frequency distribution table below;
| Length | No.of cobs |
| 12-14 | 6 |
| 14-16 | 8 |
| 16-18 | 12 |
| 18-22 | 18 |
| 22-28 | 6 |
- Calculate the mean length of the maize cobs. (3 marks)
- On the grid provided represent the information in the table above using a:
- Histogram (5 marks)
- Frequency polygon. (2 marks)
22. Two alloys P and Q, are each made of Tin, Aluminum and Copper. In alloy P, the ratio of Tin to aluminum is 2:3 and the ratio of Aluminum to Copper is 2:5.
- Determine the ratio of Tin : Aluminum : Copper in alloy P (2 marks)
- The mass of alloy P is 300Kg. Alloy Q has the same mass as alloy P but the amount of Tin is 20% less than that of alloy P. Calculate
- The mass of Tin in alloy P (2 marks)
- The total mass of Aluminum and Copper in alloy Q. (3 marks)
- Given that the ratio of Aluminium and Copper in alloy Q is 5:8, Determine the ratio of Tin: Aluminium: Copper in alloy Q. (3 marks)
23. On the grid provided below, draw triangle PQR where P(2, 3) (5, 3) and R(2,6). (1 mark)
- On the same grid, draw triangle P'Q'R', the image of PQR after an enlargement scale factor-1 centre (0, -1) (2marks)
- Triangle P"Q"R" is the image of triangle P'Q'R' after a translation vector (1)
- State the coordinates of triangle P"Q"R". (2 marks)
- Draw triangle P"Q"R" (1 mark)
- Triangle P'''Q'"R"' is the image of triangle P"Q"R" after a half turn about (0,0).
Draw triangle P'''Q'"R"' (2marks) - State two pairs of triangles that are directly congruent.(2marks)
24. Given the equation of the curve y = 8+2x-x2 fill in the table below
| x | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 |
| y |
- Use the mid-ordinate rule to estimate the area bounded by the curve y = 8+2x-x2, the lines x=-1 and x = 4,use 5 strips (2 marks)
- Use integration method to calculate the same area (4 marks)
- Find the percentage error in estimating the area using the mid ordinate rule. (2 marks)
Download Mathematics Paper 1 Questions - Alliance Girl's High School Mock December 2020.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

