Mathematics Trial Exams Paper 1 Questions - Alliance Boys High School Mock December 2020

INSTRUCTIONS TO CANDIDATES

1. Write your name and Admission number in the space provided at the top of this page.
2. The paper contains TWO sections; section I and section II
3. Answer ALL the questions in Section I and Only Five questions in Section II
4. Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
5. Marks may be given for correct working even if the answer is wrong. 
6. Non-programmable silent electronic calculators and KNEC mathematical tables maybe used.

For Examiners use only
Section I

Section I

QUESTIONS

Section 1 (50 marks): Answer all questions in this section
1. Solve; 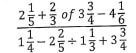(3mks)
2. The sum of two numbers is 24 while the difference of theirs squares is 144. Find the two numbers. (3mks)
3. Evaluate the value of x in; log₂x + log_x2 = 2 (4mks)
4. Simplify completely without using mathematical tables or calculator; 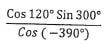(3mks)
6. The size of an interior angle of a regular polygon is 3 times that of its exterior angle. Determine the number of sides of the polygon. (3mks)
7. A man invests Ksh. 100,000 in an account which pays 16% interest per annum. The interest is compounded quarterly. Find the amount in his account after 5 years and 5 months, to the nearest shilling. (4mks)
8. use reciprocal tables to determine the values of a and b . (3mks)
9. A line segment AB is shown. Construct angle CAB = 30º. Hence use the constructed line AC to find a point T such that B divides At in the ration 5: -2
(3mks)

10. Given that the ratio x: y = 3:5, find the ratio. (2mks)
(5x – 2y) : (x + 2y)
11. Two flag posts A and B stand vertically on a level ground some distance apart, post A is 12m high. The angle of depression of the foot of post from the top of post A is 14.3°. while the angle of elevation of the top of post B from the top of the post A is 13.9. calculate the height of post B to 2d.p. (2mks)
12. Use logarithms to evaluate;
(4mks)
13. The line which joins the image of point A(4,5) under reflection in the line x = 1 and point B (3, k) is perpendicular to a line whose equation is 3y - 2x=5. Find the value of k. (3mks)
14. 

1. Draw a regular pentagon of side 4cm (1mk)
2. On the diagram drawn, construct a circle which touches all the sides of the pentagon (3mks)

15. In the figure below, O is the centre of the circle which passes through the points C, T, and D. CT is parallel to OD and line BTA is tangent to the circle at T. If the angle BTC is 44º, find the size of angle TOD. (2mks)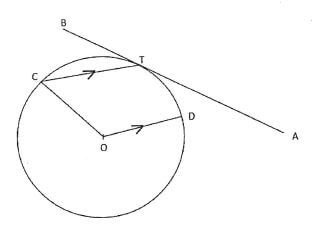

16. The figure below shows part of a circle, where chord AB-12cm, line CD=4cm and AC=CB. Calculate the area of the shaded part. (4mks)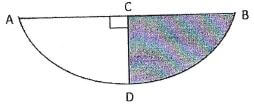

SECTION II (50 marks). Answer ONLY five questions in this section,
17. A frustrum with a regular pentagonal base is such that its top is of side 12cm and bottom is of side 24cm. If its perpendicular height is 20cm, calculate;

1. The length of the slant edge. (4 mks)
2. The volume of frustrum. (4 mks)

18. Four towns P, Q, R, and S are such that town Q is 120km due east of town P. Town R is 160km. due north of town Q. Town Sis 147km on a bearing of 330° from P and on a bearing of S75°W from R. Use a ruler and pair of compasses only for all your constructions.

1. Using a scale of 1cm represent 20km, construct a scale drawing showing the positions of PQR and s (4mks)
2. Use the scale drawing to determine;
   1. The distance from town S to town R (1mk)
   2. The bearing of town from town Q (1mk)
   3. A town T is due north of P and the distance TQ = TR. Locate T by construction and find the bearing and distance of T from R. (4mks)

19.

1. Complete the table below for the function y = 8x² - 14x - 15 (1mks)
   

   x	-2		-1	0	1	2	3	4
   y

   (3mks)
2. Draw the graph of y = 8x² - 14x - 15 for the values -2≤ x ≤ 4.
   Use the scale:
   X-axis 2cm rep 1 unit
   Y-axis 1cm rep 10 units
   
   Use your graph to solve the following equations;
   1. x²-x-2 = 0 (2mks)
   2. 2^2x+3 - 7(2^x+1)-15 = 0 (4mks)

20. In triangle AOB, OA - 12a, and OB 12 b. P and Q are points on OA and OB respectively such that 30P = OA and OQ = ¹/₃OB. M is the mid-point of AB.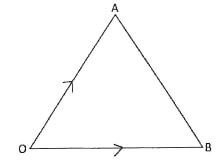

1. Express the following in terms of a and b.
   1. OM (1mk)
   2. PM (2mks
2. OM and BP intersect at Rsuch that PR = KPB and OR = hOM. Express PR in two ways and hence find the values of h and k. (4mks)
3. Show that A, R, and Q are colinear: (3 mks)

21. The distance 5 metres from a fixed point, covered by a particle after t seconds is given by the equation;

S = t³ - 6t² + 9t + 5

1. Calculate the gradient of the curve at t = 0.5 seconds. (3mks)
2. Determine the values of S at the maximum turning point of the curve. (3mks)
3. On the space provided, sketch the curve of; S = t³ - 6t² + 9t + 5 (4mks)

22. Two investors, Omwenga and Mwaniki started a business in January 2014. Omwenga invested Sh. 480,000 and Mwaniki Sh. 600,000.

1. Given that a profit of Sh. 324,000 was made in the year 2014, calculate the amount received by each of the partners if the profit was shared in proportion of their investments.(3mks)
2. in 2015 and 2016 they took salaries from the profit and they shared the remaining profits in proportion to their investments. Omwenga's salary was Sh. 90,000 and that of Mwaniki was Sh. 72,000 each year,
   1. If in the year 2015 profit was Sh. 450,000 find Omwenga's total income in 2015. (4mks)
   2. In the year 2016 Mwaniki received a total of Sh. 192,000. Calculate the profit made in the year 2016. (3mks)

23. A racing cyclist completes the uphill section of a mountainous course of 75 km at an average speed of Vkm/hr. He then returns downhill along the same route at an average speed of (+20) km/hr.

1. Given that the difference between the times spent going up and down respectively is one hour, form and solve an equation in V, hence; 
   1. Find the total time taken to complete the uphill and downhill sections of the course. (5mks)
   2. Calculate the cyclist's average speed over the 150km race. (1mk)
2. A train moving at an average speed of 72 km/hr takes 15 seconds to complete crossing a bridge that is 80m long.
   1. Express 72 km/hr in metres per second. (1mk)
   2. Find the length of the train in metres (3mks)

24. The diagram below which is not drawn to scale shows an isosceles triangle ABC in which AB-AC. The co-ordinates of A and B are (5, 6) and (0, -4) respectively.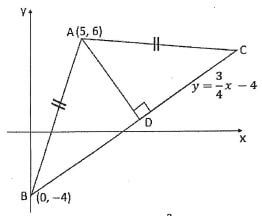

Given that the equation of the line BC is y=-x-4 and the perpendicular from A to BC meet BC at D, find;

1. The equation of AD(2mks)
2. The co-ordinates of D(2mks)
3. The co-ordinates of C(2mks)
4. The area of the triangle ABC (leaving your answerin-surd-form) (4mks)