INSTRUCTIONS TO CANDIDATES
- Write your name and Admission number in the space provided at the top of this page.
- The paper contains TWO sections; section I and section II
- Answer ALL the questions in Section I and Only Five questions in Section II
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables maybe used.
For Examiners use only
Section I
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Total |
Section I
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | Total |

QUESTIONS
SECTION I ( 50 MARKS )
Answer all the questions in this section
1. Given the conditions that log a = -1.3748 and log b = -1.5934, evaluate 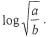 (3marks)
(3marks)
2. Simplify: 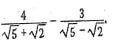 (3mks)
(3mks)
3. In the figure below, is the centre of circle QRPTS and UT is tangent to the circle at T. Given that SV=8, VP=4, PU=8 and UT=12. Find the lengths of QV and VR.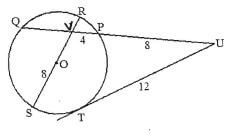 (3marks)
(3marks)
4. The volume of a cone is given as 1/3πr2 Find the percentage error in the area if the relative error in r is 0.0036 and the relative error in his 0.024. (2 marks)
5.
- Expand
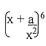 .in descending powers of x up to the term independent of x. (2 marks).
.in descending powers of x up to the term independent of x. (2 marks). - If the value the independent term is 1215, find the value of a (2 marks).
6. Solve the equation 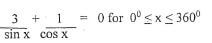 (3marks)
(3marks)
7. Ogwan'g was employed with a starting salary of Ksh. 12,560 p.m followed by increment of Ksh. 3,756 on his monthly salary every year. Determine
- His monthly salary in the 5th year. (1marks)
- The total amount Ogwang had earned by the end of his 10th year in employment (2 marks)
8. Given that OA = 3i + 4j - 6k and OB = 2i + 3j + k and that P divides AB in the ratio 3: -2,
- find AB (2marks)
- write the coordinates of P. (2 marks)
9. On the figure below, shade the locus of point P such that P is (4 marks)
- nearer to A than B.
- less than 5cm from B.
- nearer to AB than to AC.
- less than 2cm from AB
10. The table below gives the values for the curve y = 12x - 3x2 for -3 ≤ x ≤ 5.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -63 | -36 | -15 | 0 | 9 | 12 | 9 | 0 | -15 |
- use the trapezium rule with 8 trapezia to estimate the area bounded by the curve, x-axis, line x = - 3 and x = 5 (2 marks)
- use the mid-ordinate rule with 4 strips to estimate the area bounded by the curve, x-axis, line x = - 3 and x = 5. (1 marks)
11. A circle whose equation is (x+2)2 + (y-5)2 = 25 touches a straight line at (-7,3). Find the equation of the line (3marks)
12. The marks scored by 30 students in a mathematics examination are as follows:
60 54 40 67 53 73 37 55 62 43 44 69 39 32 45
48 23 60 59 47 65 58 74 47 40 59 68 51 50 50
- Prepare a frequency distribution table using the table below (2marks)
Marks Tally Frequency 21-30 31-40 41-50 51-60 61-70 71-80 - Calculate the pass mark if 70% of the students are to pass. (2 marks)
13. The angles of a triangle are in the ratio 4: 3:2. If the longest side of the triangle is 5.4cm. Calculate the length of the shortest side. (3marks)
14. The gradient of a curve at any point is given by 2x - 1. Given that the curve passes through point (1,5), find the equation of the curve. (2 marks)
15. Maken the subject of the formula given that 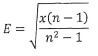 (3 marks)
(3 marks)
16. Town P(x,y) is west of town Q(15°N,24°E). If the local time at P is 0225 hours when the local time at Q is 1925 hours, find the position of P (3marks)
Section II (50 marks)
Answer five questions from this section
17. Wapesa earned a monthly salary of sh.160,000. She also received a house allowance of sh. 30,000 and a medical allowance of Sh.4,000. She is entitled to a personal relief of sh. 1056 per month Income tax charges table is shown below.
Ksh. Per month Tax rate (%)
1 - 25,000 0%
25,001 - 45,000 10%
45,001 - 70,000 15%
70,001 - 100,000 20%
100,001 - 130,000 25%
130,001 and above 30%
- Calculate her taxable income per month. (1 mark)
- How much tax does she pay per month. (6 marks)
- Calculate Wapesa's net salary per month if the following deductions are also made monthly. (3 marks)
NHIF Kshs. 4,000.
SACCO dues Kshs. 20,000
Bank loan Kshs. 80,000
18.
- A bag contains y red balls and (y-10) blue ones. The probability of drawing at random a red ball is 0.75. Find:
- The number of balls in the box. (2marks)
- The probability of drawing at random a blue ball. (1 mark)
- The probability of a candidate passing her secondary examination is 4/5. If she passes her examination the probability of her joining the university is 2/3. If she fails, her examination the probability of her joining the university is 1/4. If she joins the university the probability of her getting a job is 6/7 and if she doesn't join the university the probability of her getting a job is 2/9. Using a tree diagram, find:
- draw a tree diagram to represent the information (2 marks)
- the probability of passing her secondary examination. (1 marks)
- the probability that she joins the university. (2 marks)
- the probability that she does not get a job. (2 marks)
19. A tours and guide company hires two types of buses; X and Y. On a certain day, the company has to take 560 tourists for a trip. A type X bus has a capacity of 70 tourists and a type Y bus has a capacity of 40 tourists. The company has to hire at least 10 buses. Buses of each type must not be less than three. It costs shs. 40,000 and shs. 30,000 to hire a type X and a type Y bus respectively.
- Write down all the inequalities that represent the information above. (3 marks)
- On the graph paper provided represent the inequalities to show the required region. (4marks)

- Use your graph to determine the number of buses of each type that should be hired so as to minimise the costs. (2marks)
- Find the minimum cost. (1 mark)
20.
- Find the area of the object whose image vertices are A(4,2), B(10,2), C(10,9) and D(4,9) under a transformation matrix represented by
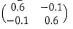 (3marks)
(3marks) - A triangle T whose vertices are A(2,3), B(5,3) and C(4,1) is mapped onto triangle T, whose vertices are A' (-4,3), B'(-1,3) and C (2,1) by a transformation M. Find;
- The transformation matrix represented by M. (3marks)
- Using the unit square, identify and describe the transformation M. (2marks)
- Triangle T2 is the image of T under a transformation N=
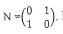 Find a single matrix that maps T onto T2. (2marks)
Find a single matrix that maps T onto T2. (2marks)
21. The figure below shows a tetrahedron OABC. Its base ABC lies on a horizontal plane and is an equilateral triangle, with sides 5cm. OA = OB=OC = 8cm. E is the midpoint of AB.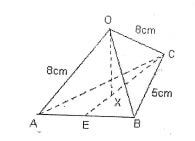
- Calculate the length, in cm to 4 significant figures of CE (2 marks)
- X is a point which divides CE in the ratio 2:1 and OX is vertical. Calculate to 4 significant figures
- Length of Ox (2 marks)
- The size of the angle, in degrees between the line OA and the plane ABC (2 marks)
- The size of the angle, in degrees between the plane. OAB and the plane ABC. (2marks)
- The size of the angle, in degrees between the plane. OAB and the line OC, (2 marks)
22.
- A quantity Q partly varies as R and partly varies as the square of R. When R=2. Q = 2 and when Q=12, R = 3. Find Q when R is 5. (3marks)
- Three quantities x, y and z are such that the square root of y varies directly as the square of x and inversely as z. find the;
- percentage change in z if x decreases in ratio 4:5 and y increases by 44% (4 marks)
- when z = 9/35, x=3 and y=196. Find y when x = 7 and z= 8 (3 marks)
23. A solution whose volume is 120 litres is made up of 35% water and the rest alcohol. When y litres of alcohol is added the percentage of water drops to 15%
- Find the value of y (4 marks)
- The new solution is diluted further by addition of seventy litres of water. Calculate the percentage of alcohol in the resulting solution (2 marks)
- A blend is made by mixing 10 litres of the solution in (b) above with 20 liters of the original solution. Calculate in the simplest form, the ratio of water to that of alcohol in the blend (4marks)
Download Mathematics Trial Exams Paper 2 Questions - Alliance Boys High School Mock December 2020.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

