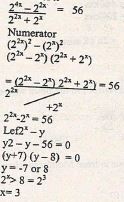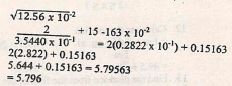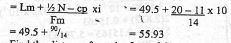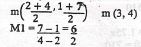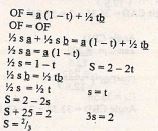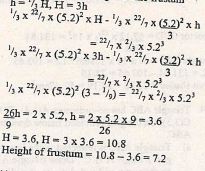Mathematics Paper 1 Questions and Answers - Sukellemo Joint Mock Examinations July 2020

INSTRUCTION TO CANDIDATES:

1. Write your name index number and class in the spaces provided at the top of this page.
2. Sign and write the dateand the name of your school in spaces provided above.
3. This paper consists of two Sections: Section I and Section II.
4. Answer all the questions in Section I and any FIVE questions from Section II
5. All answers and working must be written on the question paper.
6. Show all the steps in your calculation, giving your answer at each stage in the spaces provides below each question.
7. Marks may be given for correct working even if the answer is wrong. 
8. Non-programmable silent electronic calculators and KNEC Mathematical tables (6) edition)may be used, except where stated otherwise.
9. Candidates should check the question paper to ascertain that all the pages are printed as indicat and that no questions are missing.

FOR EXAMINER'S USE ONLY:
SECTION 1

SECTION II

QUESTIONS

SECTION I (50 MARKS)
Answer all the questions from this section.

1. Without using a calculator, evaluate 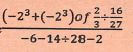(3marks) 
2. Given that 4.5 litres of water (density 1g/cm) was mixed with 12 litres of alcohol (density 0.8 g/cm³). Calculate the density of the mixture.
   (3marks)
3. Solve for x, 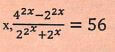 (4marks)
4. The surfaces of two cylindrical water tanks are 50 cm². and 162cm² respectively. Given that the volume of water in the second tank is 36450cm³, find the volume of water in the first tank if it is half full. (3marks)
5. Use square, reciprocal and square root tables to evaluate correct to 4sf the expression below. 
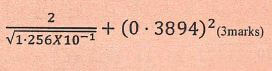
6. The interior angles of an octagon are 70°,90°, x°, 1.5x°, 130°, 80°, 1.75x° and 200°. Find the value of the largest angle (3marks)
7. A two-digit number is such that the one's digit is four more than the tens digit, and the sum of the digits is 14. Find the number (3marks)
8. Find the equation of line L₁, which is perpendicular to line 3y+2x = 6 and cuts the x-axis at -3 (3marks)
9. The price of a commodity changed in the ratio 5:4. After one month the price of the same commodity changed in the ratio 7:8. Given that the new price was 350,000, calculate the original price of the commodity. (3marks)
10. A Kenyan bank buys and sells foreign currencies as shown below:
    

    	Buying(ksh)	selling (ksh)
    1 Sterling pound (£)	130.10	130.54
    1 South Africa Rand	9.52	9.58

    A business man on a trip to Kenya had £50,000 which he converted to Kenya shillings. While in Kenya he spent 80% of the money and changed the balance to South Africa Rands. Calculate to the nearest Rand the amount he obtained. (3marks)
11. Find the range of X if x + 21 ≥ 15-2x ≥ x+12 (3marks)
12. The table below shows marks scored by 40 students in a mathematics test
    

    Marks	30-39	40-49	50-59	60-69	70-79
    No of Students	2	9	14	7	8

    Calculate the median (3marks)
13. From the window of a building a few metres from the ground an observer sees the top of a flag post at an angle of elevation 300. From the top of the flag post an eagle observes the foot of the building at the point where the window is through an angle of depression 80°. If the distance from the building to the flag post is 25m, find the distance from the foot of the building to the window (3marks)
14. ABCD is a rhombus. A is the point (2,1) and C is the point (4,7). Find the equation of the diagonal BD in the form ax + by = c(4marks)
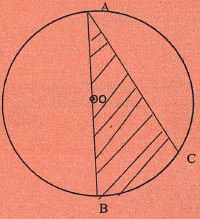
15. In the figure below, AB is the diameter of the circle. Arc BC subtends 50°at the circumference and chord AC is 4cm in length. Calculate the area of the shaded part. (3marks)
    
16. A school is 3km north of a social hall. A church is on a bearing of S48°E from the school. If the distance of the school from the church is 4km. Show their positions by construction and measure the distance and bearing of the social hall from the church. (3marks)

SECTION II (50 MARKS)
Answer any five questions from this section.

17.                    
    1. By taking integral values of x from x = -2 to x = 6make table of values for the function y = 3x(4 - x)(2marks)
       

       x	-2	-1	0	1	2	3	4	5	6
       y

    2. On the same axes and using the scale of 1 cm to 1 unit on the x-axis and 1 cm to 5 units on the y-axis, draw graphs of y = 3x(4-x), and
       y = 5(x - 2)(4marks)
       
    3. From the graph;
       1. Find the roots of the equation 3x(4-x) = 0(1mark)
       2. Write down the maximum value of y = 3x(4 - x)(1 mark)
       3. Deduce the roots of the equation 3x (4 - x) = 5(x - 2)(2marks)
18. A bus left Nairobi at 8:00am and travelled towards Mombasa at an average speed of 80km/h. At 8:30am a car left Mombasa towards Nairobi at an average speed of 120km/h. Given that the distance between Nairobi and Mombasa is 500km/h, determine:
    1. The time the car arrived in Nairobi. (2marks)
    2. The time the two vehicles met (4marks)
    3. The distance from Nairobi to the point where they met (2marks)
    4. How far the bus is from Mombasa when the car arrives in Nairobi (2marks)
19. Use a ruler and compasses only for all constructions in this question.
    1.                                  
       1. Construct a triangle ABC in which AB=8cm, and BC=7.5cm and 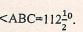(3marks)
       2. Measure length AC (1mark)
    2. By shading the wanted region show the locus of P within the triangle ABC such that
       1. AP≤BP
       2. AP>3cm
          Mark the required region as P (2marks)
    3. Construct a normal from C to meet AB produced at D (2marks)
    4. Locate the locus of point R on the same diagram such that the area of triangle ARB is ³/₄ the area of triangle ABC  (2marks)
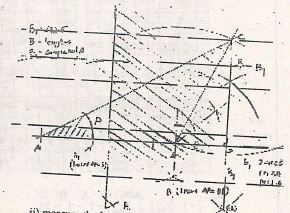
20. The displacement, s metres, of a moving particle after t seconds is given by the equation
    S = 2t³ - 5t² + 4t + 2.Determine: 
    1. The velocity of the particle when t = 3 seconds(3marks)
    2. The value of t when the particle is momentarily at rest (3marks)
    3. The displacement when the particle is momentarily at rest (2marks)
    4. The acceleration of the particle when t = 3(2marks)
21. In the figure below E is the midpoint of AB, OD:DB=2:3 and F is the point of intersection of OE and AD
    
    
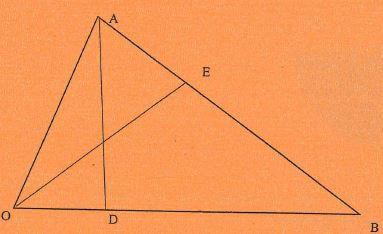
    1. Given that OA=a and OB=b, express in terms of a and b
       1. OE (1 mark)
       2. AD (1 mark)
    2. Given further that AF= tAD and OF=sOE, find the values of s and t (5marks)
    3. Hence show that O, F and E are collinear (3marks)
22. The figure below shows a cross-section of a bottle. The lower part ABC is a hemisphere of radius 5.2cm and the upper part is a frustum of a cone. The top radius of the frustum is one third of the radius of the hemisphere. The hemispherical part is completely filled with water as shown.
    
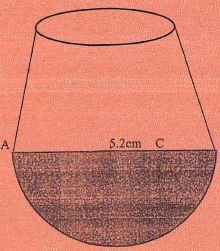
    When the container is inverted, the water now completely fills only the frustum part.
    1. Determine the height of the frustum (6marks)
    2. Find the external surface area of the bottle (4marks)
23. Two circles centres A and B have radii 20cm and 15cm respectively. If the distance between their centres AB is 30cm
    
    
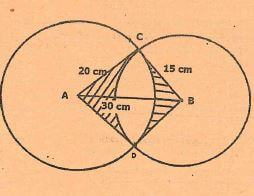
    1. Calculate
       1. The length of the common chord CD (3marks)
       2. Angle CAD(2marks)
       3. Angle CBD(2marks)
    2. Calculate the area of the commonun shaded region(3marks)
24. Triangle ABC has co-ordinates A(1,4) B(1,1) and C(3,3). On the grid provided below, draw triangle ABC (1 mark)
    
    
    1. Triangle ABC is reflected in the line x=0 to give triangle A'B'C'. Draw triangle A'B'C' on the same grid and state its co-ordinates. (3marks)
    2. Triangle A"B"C" is the image of triangle A'B'C' under a stretch with x-axis invariant and scale factor of 2. Determine the coordinates of A"B"C" and draw it on the same grid. (3marks)
    3. A(-1,7) and B(-1,4) are the images of A' and B' respectively under a shear with y-axis invariant. Determine the co-ordinates of C and draw AB "C" on the same grid.(3marks)

MARKING SCHEME

1. Evaluate Bodmas
   Numerator
   (-8 +-8)of ²/₃ +16
                          27
   -16 of ²/₃ +  16
                       27
   -16 × ²/₃  + 16
                      27
   -32  ×  27 
     3       16
   = -18
   Denominator
   -6 - ¹/₂ - 2
   -8¹/₂      -18 +-¹⁷/₂
   -18 ×  -2     =  36    
             17         17
   = 2 ²/₁₇
2. Calculate the density of the mixture D = ^m/_v
   Mass (water) =  4.5 x 1000 x 1 = 4500gms
   Mass of Alcohol = 12 x 1000 x 0.8 = 9600gms
   Total mass = 14100
   Total volume 4500 +12000 = 16500
   D = 14100
         16500
   = 0.8545g/cm³
3. Solve for x
   
4. Find volume of water in the first tank if it is half full
   ASF = 50:162
             25:81
   LSF = 5:9
   VSF-125:729
   729 = 36450
   125 = ?
   36450 x 125
            729
   = 6250cm³
5. Use square reciprocal and square root tables to evaluate
        2          +(3.894 x 10^-1)²
   
   
6.  Find value of the largest angle
   Sum of interior angle
   = (2n-4) 90
   = (16-4) 90
   =1080
   70 +90+ x + 1.5x + 130 + 80+ 1.75x+ 200= 1080
   570 +4.25x = 1080
   4.25x = 510
   X = 120
   Largest = 1.75x
   1.75 x 120 = 210
7. Find the number
   Digit No. xy
   y - x =4
   y + x = 14
   2y = 18 =y=9
   9 - x = 4
   9 - 4 = x
   X = 5
   Number = 59
8. Find the equation of line L₁
   3y + 2x = 6
   3y = -2x + 6
   Y = -²/₃x+2
   I gradient = ³/₂
   Passes (-3,0) (x, y) (-3,0)
   Y - 0  = 3
   x + 3    2
   2y = 3x +9 or y=³/₂x + ⁹/₂   or 2y - 3x = 9
9. Calculate the original price of the commodity
   The original price be = x
   x x⁵/₄ = 1.25x
   1.25x x⁷/₈ = 1.09375x or ³⁵/₃₂x
   ³⁵/₃₂x = 350,000
   x =  350.000 x 32
                   35
   = 320,000/=
10. Calculate to the nearest Rand the amount he obtained
    £1 =sh 130.10
    £50,000 = ?
    130.10 x 50,000 = Kshs 6,505,000/=
    Balance = 20 x 6,505,000 = 1,301,000
                  100
    IR = Ksh 9.58
    ? = Ksh 1,301.000
    1 x 1.301.000
          9.58
    = 135,803.76
    = 135,804
11. Find range of x
    x+21 ≥ 15 - 2x
    3x ≥ 15-21
    3x ≥ -6
    x ≥ -2
    -2 ≥ x ≥ 1
    OR
    15-2x ≥ x+12
    15-12 ≥ x + 2x
    3 ≥ 3x
    1 ≥ x
    -2 ≥ x ≥ 1
12. Calculate the median
    
    
13. Find the distance from the foot of the building to the window
    x = 25tan30 - 14.43
    y=25tan80 = 141.78
    d=141.78 - 14.43
    = 127.35m (2 dp)
14. Find equation of the diagonal BD in the form
    ax + by = c
    
    6_AB = 3
    M₁ × M₂ = -1
    3 x M2 = y
    6_BD =  -¹/₃(3,4)
    y - 4  = -1
    x - 3      3
    3y - 12 = -x +3
    x + 3y = 15
15. Calculate area of the shaded part
        1          =     4      
    Sin 50             sin 80
    = 4 sin 50
          Sin 80
    = 3.111
    Area of △ AOC = ¹/₂ × (3.111)² sin 80
    = 4.766cm²
    Area of sector OBC
    =100 x 22 x 3.111²
      360     7
    = 8.449cm³
    Area of shaded part = 4.766 +8.449
    = 13.215cm²
16. Show positions by construction and measure distance and bearing of the social hall from the church
    Distance = 2.9km
    Bearing = 263+p
    = 583°W 
17. Make table of values o functions
    y= 3x(4-x)
    Draw graphs of y = 3x(4-x), and y = 5(x-2)
    Y = 5(x-2)
    

    x	-2	0	2	4
    y	-20	-10	0	10

    
    c). from graph
    1. Find roots of the equation 3x (4-x) = 0
       x = 0, x = 4
    2. Write down maximum value of y = 3x (4 - x)
       12
    3. Deduce roots of the equation 3x(4-x = 5(x-2)
       x = -1
       x = 3.3 ± 0.1
18.                  
    1. The time the car arrived in Nairobi
       T= D = 500 = 4h 10 min
            S    120
       exact time 8.30
                   + 4.10
                 12.40pm
    2. The time the two vehicles met
       Nairobi............................... Mombasa
       Bus                                      Car
       8am; 80km/h                        8.30am; 120km/h
       D_B: 80 x ¹/₂ = 40km
       R.D = 500-40 = 460km
       R.S =  80+ 120 = 200km
       T = 460
             200
       = 2h 18 min
       Time =  8.30
                + 2.18
               10.48am 
    3. Distance from Nairobi to the point where they met
       D_N = -500 - (120 x 46)
                                    20
       = 500 - 276
       = 224km
    4. How far the bus is from Mombasa when the car arrives in Nairobi
       Time 12.40
              - 8:00
                 4.40
       D = 500 - (80 x 14)
                                3
       = 126²/₃km
19.                  
    1.                            
       1. Construct triangle ABC in which AB 8cm and BC = 7.5cm and angle ABC = 112¹/₂°
          
       2.  measure the length of AC
          13 ± 0.1
    2. By shading unwanted regions show locus P within triangle ABC such
       1. AP ≤ BP
       2.  AP > 3cm
          Mark required region as P
    3. Construct perpendicular rom C to meet AB produced tD
    4. Locate locus o R in the same diagram such that area of triangle ARB is the area of triangle ABC ³/₄ x 6.8 = 5.1cm
20. Determine
    1. Velocity of the particle when t = 3 seconds
       ds = 6t² -10 + 4
       dt
       V = 54 - 30 + 4   V=28m/s
    2. The value oft when the particle is momentarily at rest
       6t² - 10t + 4 = 0
       P = 24               S = -10 (-6,4)
       6t² -6t - 4t + 4 = 0
       6t (t-1)-4 (t-1) = 0
       (6-4) (t-1) = 0
       t  =1 or  ²/₃seconds
    3. The displacement when particle is momentarily at rest
       When t = 1  when t = ²/₃
       S = 2t³ - 5t² + 4t+2
       S = 2 - 5 + 4 + 2
       S = 3m
       
       When t = ²/₃
       S=2t³ - 5t² + 4t + 2
       S= 2(²/₃)³ - 5(²/₃)² + 4(²/₃) + 2
       S=3 ¹/₂m
    4. The acceleration of the particle when
       t = 3
       dy = a = 12t -10
       dt
       a = 36-10
       = 26m/s² 
21.                  
    1. Given that OA-a and OB=b, express in terms ofa and b
       1. ОЕ.
          OE = OA+ AE = ¹/₂a + ¹/₂b
       2. AD
          AD = AO+OD=-a + ²/₅b
    2. Given further that AF = AD and OF = SOE find values of s and t
       AF = t(²/₅b - a)
       A=²/₅tb - ta
       OF = SOE
       = s( ¹/₂a + ¹/₂b)
       ¹/₂sa + ¹/₂sb
       OF = OA + AF
       =a + ¹/₂tb - ta
       =a - ta + ¹/₂tb
       
        Therefore S = ²/₃    t= ²/₃
    3. Hence show that O, F and E are collinear
       OF = SOE
       But s=²/₃
       OF = ²/₃OE
       OF // OE
       But O is a common point hence collinear
22.                                
    1. Determine the height of the frustum
       h = ¹/₃H , H = 3h
       
    2. Find the external surface area of the bottle area of circular part
       
23.                            
    1. Calculate
       1. The length of the common chord CD
          h² = 15² - x=  225x x²
          h² = 20² -(30 - x)
          h² = 400 - [900 - 60x + x²]
          h² = 400 - 900 + 60x - x²
          h² = 500 + 60x - x²
          225 - x² =  -500 + 60x - x²
          725 = 60x
          x = 12.5cm
          h² = 225 - (12.5)²
          h² = 68.75
          h = √68.75 = 8.292
          therefore CD = 2 x 8.292
                        CD= 16.584cm
       2. Angle CAD
          CAY
          30 - 12.5 = 17.5
          Tan △ = 8.292
                      17.5
          △ = Tan^-1(^8.292/_17.5) = 25.35
          Angle CAD = 25.35 x 2 = 50.70°
       3. Angle CBD
          Tan = 8.292
                    12.5
          △ = Tan^-1(^8.292/_17.5)
          = 33.56
          Angle CBD = 33.56 x 2 = 67.12°
    2. Calculate area of the common un shaded region
       A. of sector ACD = 50.70 x ²²/₇ x 20² = 177.05cm²
                                     360
       A of angle ACD = ¹/₂x 20 x 20sin 50.70 = 154.77
       A                    a of K = 177.05 - 154.77 = 22.28cm²
       A of sector CBD = 67.12 x ²²/₇ x 15² = 131.84
                                    360
       A of angle CBD= ¹/₂ x 15 x 15sin67.12 - 103.65
       A of L = 131.84-103.65 = 28.19
       Total un shaded = 22.28 + 28.19 = 50.47cm²
24. Triangle ABC has co-ordinates A(1,4), B(1,1 and C(3,3). On the grid provided below draw triangle ABC.
    1. Triangle ABC is reflected in the line x=0 to give triangle A'B'C'. Draw triangle A'B'C' on the same grid and state its co-ordinates 
    2. Triangle A"B"C" is the image of triangle A'B'C' under a sketch with x-axis invariant and scale factor of 2. Determine the coordinates of A"B"C" and draw it on the same grid
    3. A(-1,7) and B(-1,4) are the images of A' and B' respectively under a shear with y-axis invariant. Determine the co-ordinates of C and draw A'B'C' on the same grid