INSTRUCTIONS
- Write your name, class, admission number, school, date and signature in spaces provided above.
- The paper contains two sections A and B.
- Answer all questions in section A and any five questions from section B in the spaces provided below each question.
- Show all the steps in your calculations giving your answers at each stage in the spaces below each question.
- Non-programmable silent electronic calculator and mathematical tables may be used except where stated otherwise.
SECTION A (50 MARKS)
(Answer all questions in this section in the spaces provided)
- Use logarithm table to evaluate. (4mks)
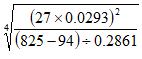
- Three sisters, Ann, Beatrice and Caroline together invested Ksh. 48,000 as capital and started a small business. If the share of profit is Ksh. 2,300, Ksh. 1,700 and Ksh. 800 respectively, shared proportionally. Find the capital invested by each of them. (3mks)
- Make t the subject of formula in x=(p+t)1/3 (3mks)
t - Without using a calculator or mathematical tables, express √3 in surd form and simplify. (3mks)
1 - cos30º - Expand and simplify (3x-y)4 hence use the first three terms of the expansion to approximate the value of (6-0.2)4. (4mks)
- Find x without using tables if 3 + log23 + log2x = log25 +2 (3mks)
- Find the value of m for which the matrix transforms an object into a straight line. (3mks)
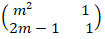
- In the figure below PT is a tangent to the circle at T, PQ = 9cm, SA = 6cm, AT = 8cm and AR = 3cm. Calculate the length of;
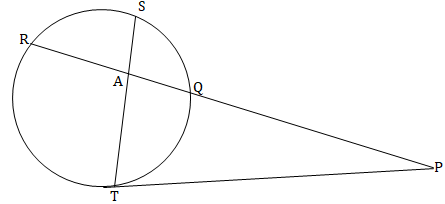
- AQ (2mks)
- PT (1mk)
- A right angled triangle has a base of 15.3 cm and height 7.2 cm, each measured to the nearest 3 mm. Determine the percentage error in finding the area of the triangle, giving your answer to 2 decimal places. (3mks)
- Given that sin x=0.8, without using a mathematical table and calculator find tan(90-x) (3mks)
- The point B(3,2) maps onto B1(7,1) under a translation T1. Find T1 (2mks)
- Using a ruler and a pair of compasses only, construct triangle ABC in which BC=6cm, AB= 8.8cm and angle ABC= 22.5º. (3mks)
- Two grades of tea A and B, costing sh 100 and 150 per kg respectively are mixed in the ratio 3:5 by mass. The mixture is then sold at sh 160 per kg. Find the percentage profit on the cost price. (3mks)
- The first, the third and the ninth term of an increasing AP, makes, the first three terms of a G.P. If the first term of the AP is 3, find the difference of the AP and common ratio of GP. (4mks)
- The matrix M=
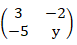 maps a triangular object of area 7 square units onto one with area of 35 square units. Find the value of x. (4mks)
maps a triangular object of area 7 square units onto one with area of 35 square units. Find the value of x. (4mks) - The equation of a circle is given by x2+4x+y2-2y-4=0. Determine the centre and radius of the circle (3mks)
SECTION B (50 MARKS)
(Answer any five questions in this section)
- A bag contains 3 black balls and 6 white balls. If two balls are drawn from the bag one at a time, find the:
- Probability of drawing two white balls:
- With replacement (2mks)
- Without replacement (2mks)
- Probability of drawing a black ball and white ball:
- With replacement (3mks)
- Without replacement. (3mks)
- Probability of drawing two white balls:
- In the triangle below P and Q are points on OA and OB respectively such that OP:PA = 3 : 2 and OQ : QB = 1 : 2. AQ and PQ intersect at T. Given that OA = a and OB = b.
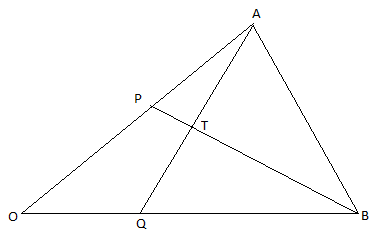
- Express AQ and PQ in terms of a and b. (2mks)
- Taking BT=kBP and AT=hAQ where h and k are real numbers.
- Find two expressions for OT in terms of a and b. (2mks)
- Use the expression in b(i) above to find the values of h and k. (4mks)
- Give the ratio BT:TP. (2mks)
- Complete the table below for the functions y=3cosx-2 for 0º≤x≤360º (2mks)
x 0 30 60 90 120 150 180 210 240 270 300 330 360 y=3cosx-2 - Plot the graph of y=3cosx-2 in the graph provided below. (3mks)

- From the graph
- Find the amplitude of the wave. (2mks)
- The period of the wave. (1mk)
- Find the solution to 3cosx=2 (2mks)
- Plot the graph of y=3cosx-2 in the graph provided below. (3mks)
- A plane leaves an airport A (41.5ºN, 36.4ºW) at 9:00am and flies due north to airport B on latitude 53.2ºN. Taking π as 22/7 and the radius of the earth as 6370Km,
- Calculate the distance covered by the plane in km (4mks)
- The plane stopped for 30minutes to refuel at B and flew due east to C, 2500km from B. Calculate:
- position of C (3mks)
- The time the plane lands at C if its speed is 500km/h (3mks)
- The curve given by the equation y=x2+1 is defined by the values in the table below.
- Complete the table by filling in the missing values. (2mks)
x 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 y 1.0 2.0 5.0 10.0 17.0 26.0 37.0 - Sketch the curve for y=x2+1 for 0≤x≤6 (2mks)
- Use the mid-ordinate rule with 5 ordinates to estimate the area of the region bounded by the curve y=x2+1, the x-axis, the lines x = 0 and x = 6. (2mks)
- Use method of integration to find the exact value of the area of the region in (c) above. (2mks)
- Calculate the percentage error involved in using the mid-ordinate rule to find the area. (2mks)
- Complete the table by filling in the missing values. (2mks)
-
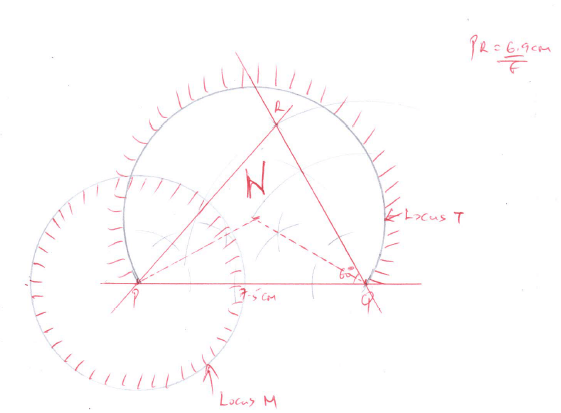
- Using a ruler and pair of compasses only construct triangle PQR in which
PQ = 7.5cm QR= 6.0cm and angle PQR = 60º. Measure PR (3mks) - On same side of PQ as R
- Determine the locus of a point T such that angle PTQ = 60º (3mks)
- Construct the locus of M such that PM = 3.5cm. (2mks)
- Identify the region W such that PR≥3 and angle PTQ≥60º by shading the unwanted part. (2mks)
- Using a ruler and pair of compasses only construct triangle PQR in which
- OABCD is a right pyramid on a rectangular base with AB = 8 cm, BC = 6 cm,
OA = OB = OC = OD = 13 cm. Calculate;- the height of the pyramid. (3mks)
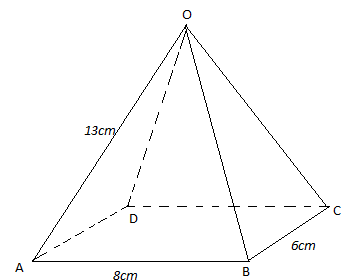
- the inclination of OBC to the horizontal. (2mks)
- the angle between;
- OB and DC (3mks)
- the planes OBC and OAD (2mks)
- the height of the pyramid. (3mks)
- The games master wishes to hire two matatus for a trip. The operators have a Toyota which carries 10 passengers and a Kombi which carries 20 passengers. Altogether 120 people have to travel. The operators have only 20litres of fuel and the Toyota consumes 4 litres on each round trip and the Kombi 1 litre on each round trip. If the Toyota makes x round trips and the kombi y round trips;
- write down four inequalities in x and y which must be satisfied . (2mks)
- Represent the inequalities graphically on the grid provided. (3mks)

- The operators charge shs.100 for each round trip in the Toyota and shs.300 for each round trip in the kombi;
- determine the number of trips made by each vehicle so as to make the total cost a minimum. (4mks)
- find the minimum cost. (1mk)








MARKING SCHEME
SECTION A (50 MARKS)
(Answer all questions in this section in the spaces provided)
- Use logarithm table to evaluate. (4mks)

- Three sisters, Ann, Beatrice and Caroline together invested Ksh. 48,000 as capital and started a small business. If the share of profit is Ksh. 2,300, Ksh. 1,700 and Ksh. 800 respectively, shared proportionally. Find the capital invested by each of them. (3mks)
A:B:C
2300:1700:800
23:17:8
23/48 : 17/48 : 8/48
Ann = 23/48 x 48000 = sh 23000
Beatrice = 17/48 x 48,000 = sh17000
Caroline = 8/48 x 48000 = sh8000 - Make t the subject of formula in x=(p+t)1/3 (3mks)
t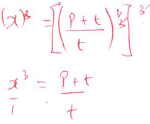
x 3 =p + t
1 t
x3t = p + t
x3t - t = p
t(x3 - 1) = p
(x3 - 1) x3 - 1
t = p
(x3 - 1) - Without using a calculator or mathematical tables, express √3 in surd form and simplify. (3mks)
1 - cos30º
(√3) 2
(1 -√3/2)2
2√3 (2+√3)
(2-√3)(2+√3)
4√3 + 6
4 - 3
4√3 + 6
1
=4√3 + 6 - Expand and simplify (3x-y)4 hence use the first three terms of the expansion to approximate the value of (6-0.2)4. (4mks)
1(3x)(-y)+4(3)(-y)+6(3x)(-y)+4(3x)(-y)+3(3x)(-y)
81x4+-108x3y+54x2y2-12xy3+y4
81x4-108x3y+54x2y2-12xy3+y4
3x=6 -4=-0.2
x=2 y=0.2
81x4-108x3y+54x2y2
81(2)4-(108.8.0.2)+(54.4.0.4)
324-172.8+8.6 4
=159.84 - Find x without using tables if 3 + log23 + log2x = log25 +2 (3mks)
3(log22)+log23+log2x = log25 + 2(log22)
log28 + log23+log2x=log25+log24
log2(8 × 3 × x)= log2(5 x 4)
24x =20 5
24 24
x = 5/6 - Find the value of m for which the matrix transforms an object into a straight line. (3mks)
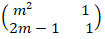
(m2 x 1)-(2m - 1)1 = 0
m2-(2m-1)= 0
m2-2m+1=0
(m2-m)(m+1)=0
m(m-1)-1(m-1)=0
(m-1)(m-1) = 0
m-1=0 m-1=0
m=1 m=1 - In the figure below PT is a tangent to the circle at T, PQ = 9cm, SA = 6cm, AT = 8cm and AR = 3cm. Calculate the length of;
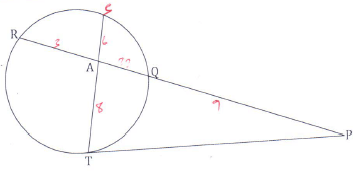
- AQ (2mks)
8 x 6 =3 x Q
3 3
AQ=16cm - PT (1mk)
9 x 28 = PT2
PT = √9 x 25
= √252
=15.8745cm
- AQ (2mks)
- A right angled triangle has a base of 15.3 cm and height 7.2 cm, each measured to the nearest 3 mm. Determine the percentage error in finding the area of the triangle, giving your answer to 2 decimal places. (3mks)
Actual area = 15.3 x 2.2 = 110.16
Max area = 15.45 x 2.35 = 113.5575
Min area = 15.15 x 7.25 = 106.8075
(E)= =106.8075 - 113.5575
2
= 6.75 = 3.375
2
%E = (E) x 100
A.A
=3.375 x 100
0.16
=3.063725490196078
=3.06 - Given that sin x=0.8, without using a mathematical table and calculator find tan(90-x) (3mks)
sinx= 8/10 = 4/5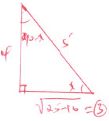
tan(92 - x) = 0/A
= 3/4 - The point B(3,2) maps onto B1(7,1) under a translation T1. Find T1 (2mks)
T1 = T' - T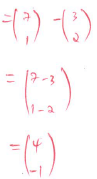
- Using a ruler and a pair of compasses only, construct triangle ABC in which BC=6cm, AB= 8.8cm and angle ABC= 22.5º. (3mks)
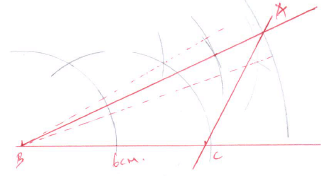
- Two grades of tea A and B, costing sh 100 and 150 per kg respectively are mixed in the ratio 3:5 by mass. The mixture is then sold at sh 160 per kg. Find the percentage profit on the cost price. (3mks)
3/8(100)+5/8(150) = Cost price
37.5 + 93.75 = sh131.25
profit = 100 - 131.25
profit = 100 - 131.25
= sh 28.75
%profit =profit x 100
c.p
= 28.75 x 100
131.25
= 21.904619
= 21.9048% - The first, the third and the ninth term of an increasing AP, makes, the first three terms of a G.P. If the first term of the AP is 3, find the difference of the AP and common ratio of GP. (4mks)
a, a+2d, a+8d
3, 3+2d, 3+8d
3+8d =3+2d
3+2d 3
a+24d = a+12d+4d2
0=4d2-12d
0=d(d-3)
4d=0 d-3=0
d=0 d=3
8=3+2(3)
3
=3+6
3
= a/3
= 3 - The matrix M= maps a triangular object of area 7 square units onto one with area of 35 square units. Find the value of x. (4mks)
def = A.S.F
A.S.F = IA
OA
= 35
7
= 5
5=3y-10
15=3y
y=5 - The equation of a circle is given by x2+4x+y2-2y-4=0. Determine the centre and radius of the circle (3mks)
x2+4x+(4/2)+y2-2y+(-2/2)2=4+4+1
(x+2)2+(y-1)2=32
(x-a)2+(y-b)2=82
(a,b)=(-2,1) x=3 units
SECTION B (50 MARKS)
(Answer any five questions in this section)
- A bag contains 3 black balls and 6 white balls. If two balls are drawn from the bag one at a time, find the:
- Probability of drawing two white balls:
- With replacement (2mks)
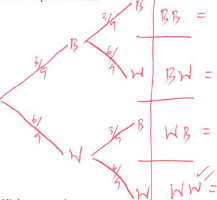
- Without replacement (2mks)
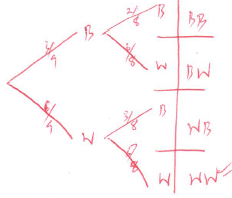
- With replacement (2mks)
- Probability of drawing a black ball and white ball:
- With replacement (3mks)
P(BW) P(WB)
=(1/9 x 6/8) + (6/9 x 2/8)
= 2/9 + 2/9 = 4/9 - Without replacement. (3mks)
= 1/4 + 1/4
= 1/2
- With replacement (3mks)
- Probability of drawing two white balls:
- In the triangle below P and Q are points on OA and OB respectively such that OP:PA = 3 : 2 and OQ : QB = 1 : 2. AQ and PQ intersect at T. Given that OA = a and OB = b.
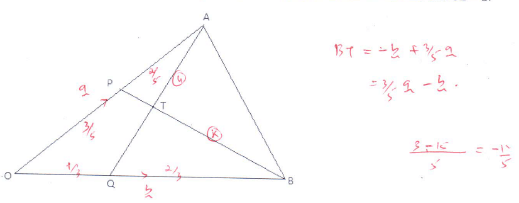
- Express AQ and PQ in terms of a and b. (2mks)
AQ = AQ + OQ
=-a + 1/3b
= 1/3b - a
PQ = -3/5.a + 1/3b
= 1/3b - 3/5a - Taking BT=kBP and AT=hAQ where h and k are real numbers.
- Find two expressions for OT in terms of a and b. (2mks)
OT = OA + AT
a+h(1/3b-a)
a+1/3hb - ha
=(1-h)a + 1/3hb
OT = OB + BT
b + k(3/5 a - b)
b + 3/5 ka - kb
(1-k)b + 3/5 ka - Use the expression in b(i) above to find the values of h and k. (4mks)
(1 - h) = 3/5k
1/3h = 1-k
h=3-3k
1-(3-3k) = 3/5 k
1-3+3k = 3/5 k
-2 = 3/1k + 3/5 k
k = 5/6
h=3-3k
=3-3(5/6)
= 3 - 5/2
h = ½
- Find two expressions for OT in terms of a and b. (2mks)
- Give the ratio BT:TP. (2mks)
BT:TP
K:1-K
5/6:1-5/6
6 x 5/6 : 1/6 x 6
BT:TP=5:1
- Express AQ and PQ in terms of a and b. (2mks)
- Complete the table below for the functions y=3cosx-2 for 0º≤x≤360º (2mks)
x 0 30 60 90 120 150 180 210 240 270 300 330 360 y=3cosx-2 1.0 -1.5 -4.9 -3.3 0.4 0.1 -3.8 -43.7 -1.0 1.0 -2.1 -5.0 -2.9 - Plot the graph of y=3cosx-2 in the graph provided below. (3mks)
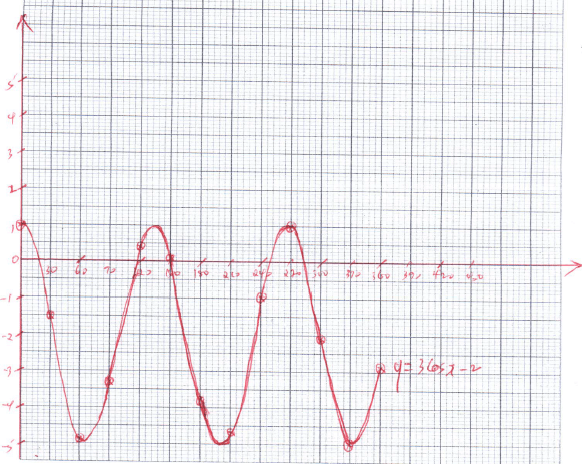
- From the graph
- Find the amplitude of the wave. (2mks)
1--5 = 3units
2 - The period of the wave. (1mk)
270º - Find the solution to 3cosx=2 (2mks)
3cosx-2=0
18º,117º,150º,249,282
- Find the amplitude of the wave. (2mks)
- Plot the graph of y=3cosx-2 in the graph provided below. (3mks)
- A plane leaves an airport A (41.5ºN, 36.4ºW) at 9:00am and flies due north to airport B on latitude 53.2ºN. Taking π as 22/7 and the radius of the earth as 6370Km,
- Calculate the distance covered by the plane in km (4mks)
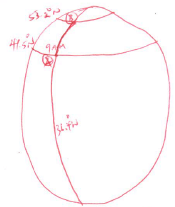
Distane =11.7 x 2 x22 x 6370
360 7
=1301.3km - The plane stopped for 30minutes to refuel at B and flew due east to C, 2500km from B. Calculate:
- position of C (3mks)
θ/360 x 2 x 22/7 x 6370cos53.32 = 2500
66.6247θ = 2500
66.6247 66.6247
θ = 37.52
36.4 - 22.97 = 13.43º
C(53.2ºN,13.43ºW)
37.52-36.4=1.12º
C(53.2ºN,1.12ºE) - The time the plane lands at C if its speed is 500km/h (3mks)
t = d/s
1,301.3 + 2500
500 500
= (2hrs 36min)+5hrs
=7hrs 36mins
37.52ºx4 = 150.08
2hrs 30mins
- position of C (3mks)
- Calculate the distance covered by the plane in km (4mks)
- The curve given by the equation y=x^2+1 is defined by the values in the table below.
- Complete the table by filling in the missing values. (2mks)
x 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 y 1.0 1.25 2.0 3.25 5.0 7.25 10.0 13.25 17.0 21.25 26.0 31.25 37.0 - Sketch the curve for y=x2+1 for 0≤x≤6 (2mks)
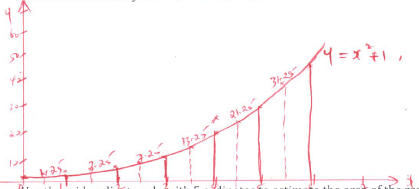
- Use the mid-ordinate rule with 5 ordinates to estimate the area of the region bounded by the curve y=x2+1, the x-axis, the lines x = 0 and x = 6. (2mks)
A=1(1.25+3.25+7.25+13.25+21.25+31.25)
=1(77.5)
=77.5 sqr units - Use method of integration to find the exact value of the area of the region in (c) above. (2mks)
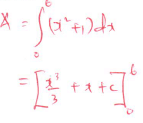
(216 + 6 + cc)
3
= 72+6+c-6
=78 sqr units - Calculate the percentage error involved in using the mid-ordinate rule to find the area. (2mks)
E = Appr A - Actual A
=77.5 - 78
=0.5sqr units
E = E x 100
A.A
=0.5 x 100
78
=0.64102564125641
=0.6410
- Complete the table by filling in the missing values. (2mks)
-
- Using a ruler and pair of compasses only construct triangle PQR in which PQ = 7.5cm QR= 6.0cm and angle PQR = 60º. Measure PR (3mks)
- On same side of PQ as R
- Determine the locus of a point T such that angle PTQ = 60º (3mks)
- Construct the locus of M such that PM = 3.5cm. (2mks)
- Identify the region W such that PR≥3 and angle PTQ≥60º by shading the unwanted part. (2mks)
- OABCD is a right pyramid on a rectangular base with AB = 8 cm, BC = 6 cm,
OA = OB = OC = OD = 13 cm. Calculate;- the height of the pyramid. (3mks)
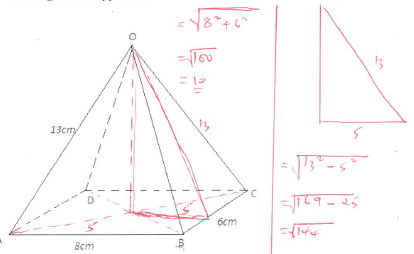
- the inclination of OBC to the horizontal. (2mks)
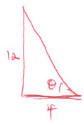
Tanθ= 12/4
θ = Tan-13
= 71.57º - the angle between;
- OB and DC (3mks)
cosB = 4/13
B = cos-1 4/13
= 72.08º - the planes OBC and OAD (2mks)
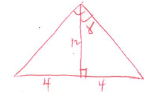
Tan = 4/12
Tan-1 4/12
= 18.43º
= 36.87º
- OB and DC (3mks)
- the height of the pyramid. (3mks)
- The games master wishes to hire two matatus for a trip. The operators have a Toyota which carries 10 passengers and a Kombi which carries 20 passengers. Altogether 120 people have to travel. The operators have only 20litres of fuel and the Toyota consumes 4 litres on each round trip and the Kombi 1 litre on each round trip. If the Toyota makes x round trips and the kombi y round trips;
- write down four inequalities in x and y which must be satisfied . (2mks)
10x + 204 ≥ 120
4x + 4 = 20
x ≥ 0
4 ≥ 0 - Represent the inequalities graphically on the grid provided. (3mks)
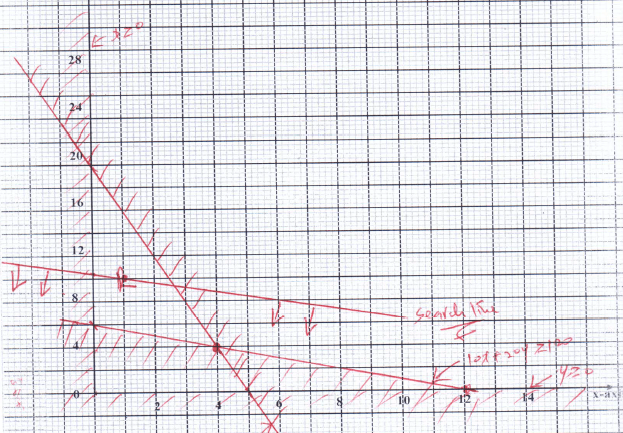
- The operators charge shs.100 for each round trip in the Toyota and shs.300 for each round trip in the kombi;
- determine the number of trips made by each vehicle so as to make the total cost a minimum. (4mks)
100x + 30y = k
100(1) + 300(10) = k
100 + 3000 = k
k = 5100
100 x + 300y =3100
3100 3100 3100
x + 4 = 1
31 10.3
Minimun cost (4,-4)
4 toyota trips
4 kombi trips - find the minimum cost. (1mk)
100x + 300y = cosy
100(4) + 300(4) = 400 + 1200
=sh1600
- determine the number of trips made by each vehicle so as to make the total cost a minimum. (4mks)
- write down four inequalities in x and y which must be satisfied . (2mks)
Download Mathematics Paper 2 Questions and Answers - Kassu Joint Mock Examination 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students