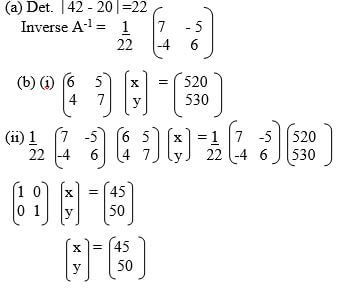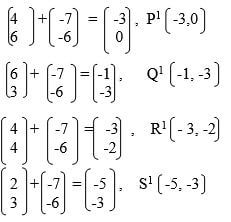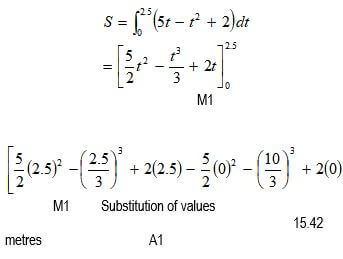INSTRUCTIONS TO CANDIDATES
- Write your name and indexnumberin the spaces provided above.
- Sign and write date of examination in the spaces provided above.
- This paper consists of two sections; Section I and Section II.
- Answer All questions in Section I andonly Fivequestions from section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations giving answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Candidates should answer questions in English.
For examiner’s use only.
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |
GRAND TOTAL __________

QUESTIONS
SECTION 1 (50 MARKS)
- Without using a calculator evaluate:- (3 marks)
-2(5 + 3) – 9 ÷ 3 +5
-3 + -16 ÷ -8 x 4 - Wafula uses 1/6 of his land for planting maize, 1/12 for beans and 4/9 of the remainder for grazing. He still has 10 hectares of unused land. Find the size of Wafula’s land. (4 mks)
- A straight line passing through point (-3,-4)is perpendicular to the line whose equation is 2y + 3x = 11 and intersects x axis and y axis at A and B respectively. Determine the equation of the second line and hence write down the co-ordinates of A and B. (3 mks)
- A bus left Kitale at 8.00 a.m. and travelled towards Lodwar at an average speed of 80 km/h. At 8.30 a.m a car left Lodwar towards Kitale at an average speed of 120km/h. Given that the distance between Kitale and Lodwar is 400km. Calculate the time the two vehicles met. (3 mks)
- The sum of four consecutive odd integers is greater than 24. Determine the first four such integers. (3 mks)
- Wanyama on arrival in Kenya to play for Harambee Stars against Uganda Cranes converted 6000 Euros into Kenyan Shillings. During his stay in Kenya he spent Kshs. 260,000 and converted the remaining amount into US Dollars before travelling back to England. Using the exchange rates below, find how many US Dollars he got? (4 mks)
Currency Buying Selling
(Kshs.) (Kshs.)
1 US Dollar 96.20 96.90
1 Euro 112.32 112.83 - In the diagram below, the position vector of points A and B with respect to point O are [-6] and [-3] respectively.
[-2] [ 0]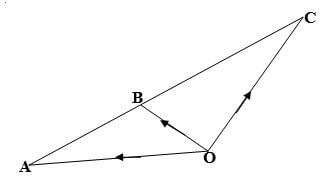
Given that B is a point on AC such that AB = ½ BC. Use vector method to determine the coordinates of C. (3 mks) - Simplify:-
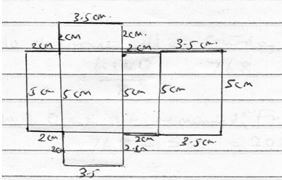
(8y)2/3 x y11/3 -6 ÷ 2y-2 - Complete the diagram below so as to make a net for a cuboid. Hence find the surface area of the cuboid. (3 mks)
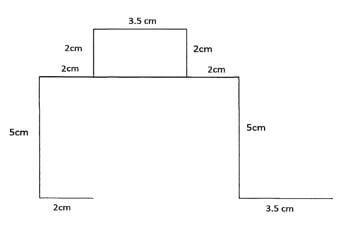
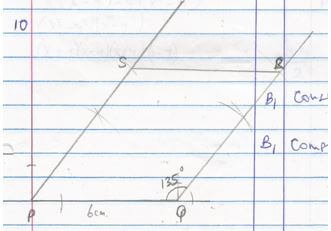
- Using a ruler and a pair of compasses only, construct a rhombus PQRS such that PQ = 6 cm and angle PQR = 135º hence measure the shortest diagonal. (3mks)
- Janice, a fruit vendor obtained a total of Kshs. 6144 from her sales of oranges on Saturday at Kshs. 8.00 each. She had bought 560 more oranges to add to what had remained on Friday where she had sold 240 more oranges than on Thursday. She had sold 750 oranges on Thursday. Calculate the total number of oranges Janice had bought on Thursday. (4 mks)
- Factorise Completely:-
x4 – 2x2y2 + y4 (2 mks) - Solve for y given that y is acute and sin (3y – 50º) – cos (2y + 10º) = 0 (3 mks)
- A solid consists of a cone and a hemisphere. The common diameter of the cone and the hemisphere is 12 cm and the slanting height of the cone is 10 cm. Calculate correct to two decimal places, the surface area ofthe solid. (3 mks)
- The figure below shows two sectors in which AB and CD are arcs of concentric circles centre O. Angle AOB = 2/5 radians and AD = BC = 5 cm.
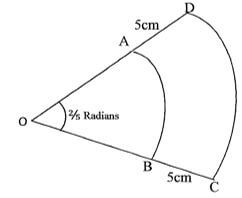
Given that the perimeter of the shape ABCD is 24 cm, calculate the length of OA. (3 mks) - Find the inequalities that define the region R shown in the figure below. (3 marks)
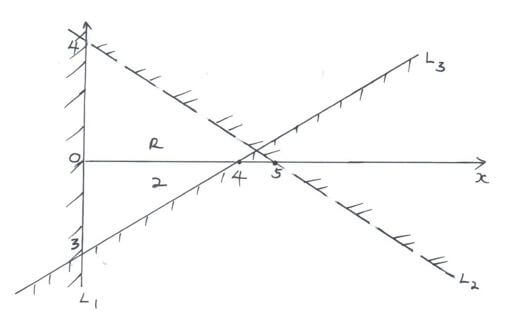
SECTION II
Answer only five questions from this section
- Nyongesa is a sales executive earning a salary of Kshs. 120,000 and a commission of 8% for the sales in excess of Kshs. 1,000,000. If in January he earned a total of Kshs. 480,000 in salaries and commission.
- Determine the amount of sales he made in the month of January. (4 mks)
- If the total sales in the month of February increased by 18% and in the month of March dropped by 30% respectively;
Calculate:-- Nyongesa’s commission in the month of February. (3 mks)
- His total earning in the month of March. (3 mks)
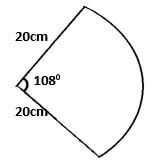
- A sector of angle 1080 is cut from a circle of radius 20 cm. It is folded to form a cone.
Calculate:- The curved surface area of the cone. (2 mks)
- The base radius of the cone. (2 mks)
- The vertical height of the cone. (2 mks)
- If 12 cm of the cone is chopped off to form a frustrum as shown below.
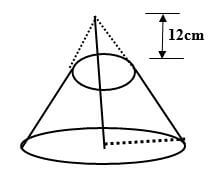
Calculate the volume of the frustum formed. (2 mks)
-
- Find A-1, the inverse of matrix
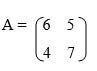 (2 mks)
(2 mks) - Ibanda sells white and brown loaves of bread in his kiosk. On a certain day he sold 6 white loaves of bread and 5 brown ones for a total of Kshs. 520. The next day he sold 4 white loaves and 7 brown ones for a total of Kshs. 530.
- Form a matrix equation to represent the above information. (1 mk)
- Use matrix method to find the price of a white loaf of bread and that of a brown loaf of bread. (3 mks)
- A school canteen bought 240 white loaves of bread and 100 brown loaves of bread. A discount of 10% was allowed on each white loaf whereas a discount of 13% was allowed on each brown loaf of bread. Calculate the percentage discount on the cost of all the loaves of bread bought. (4 mks)
- Find A-1, the inverse of matrix
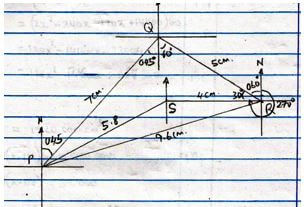
- A village Q is 7 km from village P on a bearing of 045º. Village R is 5 km from village Q on a bearing of 120º and village S is 4 km from village R on a bearing of 270º.
- Taking a scale of 1 m to represent 1 Km, locate the three villages. (3 mks)
- Use the scale drawing to find the:
- Distance and bearing of the village R from village P. (2 mks)
- Distance and bearing of village P from village S. (2 mks)
- Area of the polygon PQRS to the nearest 4 significant figures. (3 mks)
- The figure below shows a rectangular sheet of metal whose length is twice its width.
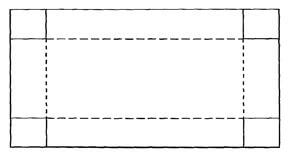
An open rectangular tank is made by cutting equal squares of length 60 cm from each of its four corners and folding along the dotted lines shown in the figure above. Given that the capacity of the tank so formed is 1920 litres and the width of the metal sheet used was x cm;-
- Express the volume of the tank formed in terms of x cm. (3 mks)
- Hence or otherwise obtain the length and width of the sheet of metal that was used. (3 mks)
- If the cost of the metal sheet per m2 is Kshs 1000 and labour cost for making the tank is 300 per hour. Find the selling price of the tank in order to make a 30% profit if it took 6 hours to make the tank. (4 mks)
-
-
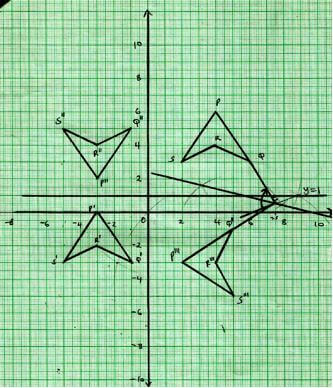
- On the Cartesian plane below, draw the quadrilateral PQRS with vertices
P(4,6), Q(6,3), R(4,4), and S(2,3) (1 mk)
- Draw P'Q'R'S' the image of PQRS under the transformation defined by the translation vector
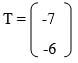 .Write down the coordinates of P'Q'R'S'. (2 mks)
.Write down the coordinates of P'Q'R'S'. (2 mks) - P''Q''R''S'' is the image of P'Q'R'S' when reflected in the line y= 1. On the same plane, draw P''Q''R''S''. (2 mks)
- Draw P'''Q'''R'''S''' the image P''Q''R''S'' when reflected in the line y – x = 0 (2 mks)
- Find by construction, the centre of the rotation that maps P'''Q'''R'''S''' onto PQRS and hence determine the coordinates of the centre of the rotation and the angle of the rotation. (3 mks)
- On the Cartesian plane below, draw the quadrilateral PQRS with vertices
- Andai recorded data on observation of time spent by a local university’s first year bachelor of Commerce students at library as follows;-
Calculate:Time spent in minutes
11 – 20
21- 30
31 – 40
41 – 50
51 - 60
Cumulative frequency
70
170
370
470
500
- The mean (6 mks)
- The median (4 mks)
-
- After t seconds, a particle moving along a straight line has a velocity of Vm/s and an acceleration of (5 – 2t)m/s². the particles initial velocity is 2m/s.
- Express V in terms of t. (3 marks)
- Determine the velocity of the particle at the beginning of the third second. (2 marks)
- Find the time taken by the particle to attain maximum velocity and the distance it covered to attain the maximum velocity. (5 marks)
- After t seconds, a particle moving along a straight line has a velocity of Vm/s and an acceleration of (5 – 2t)m/s². the particles initial velocity is 2m/s.

MARKING SCHEME
|
SOLUTION |
MARK |
COMMENTS |
|
|
1. |
-2 (5 +3) – 9 ÷ 3 +5 |
M1 M1 A1 |
Numerator |
|
3 |
|||
|
2. |
1 + 1 = 2 + 1 = 3 |
B1 B1 M1 A1 |
Fraction for grazing Fraction for unused land. |
|
4 |
|||
|
3. |
2y + 3x = 11 |
B1 B1 B1 |
Check equivalents. For both coordinates of A and B. |
|
3 |
|||
|
4. |
Kitale 400 km Lodwar |
B1 B1 B1 |
Must have units |
|
3 |
|||
|
5. |
x + x + 2 + x + 4+x + 6 > 24 |
M1 A1 B1 |
All four correct |
|
3 |
|||
|
6. |
1 Euro = ksh 112.32 |
M1 A1 M1 A1 |
|
|
7. |
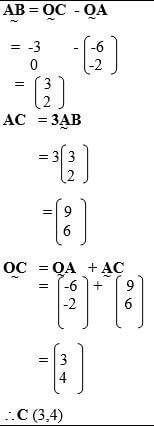 |
M1 M1 A1 |
|
|
3 |
|||
|
8. |
(8y)2/3 x y11/3 -6 ÷ 2y-2 |
M1 M1 A1 |
|
|
3 |
|||
|
9. |
|
B1 M1 A1 |
Complete and √ labelled diagram |
|
3 |
|||
|
10. |
|
B1 B1 B1 |
Construction of ∠450 Completetion of PQRS. Measure of the shortest diagnol SQ. |
|
3 |
|||
|
11. |
No. of oranges sold on Saturday; |
M1 M1 M1 A1 |
√ division √ subtraction √ Addition |
|
4 |
|||
|
12. |
x4 – x2y2 – x2y2 + y4 |
M1 A1 |
Award marks for working by inspection |
|
2 |
|||
|
13. |
Sin (3y – 500) = cos (2y + 100) |
M1 M1 A1 |
|
|
3 |
|||
|
14. |
S.A of solid = prl + 2pr2 |
M1M1 A1 |
Exp. Of areas Addition of areas |
|
3 |
|||
|
15. |
Length of an arc = θ cr |
M1 M1 A1 |
Perimeter Solving |
|
3 |
|||
| 16 |
L1 = χ ≥ 0 |
B1 | |
|
3 |
|||
|
17. |
|
M1 M1 M1 A1 M1 M1 A1 M1 M1 A1 |
Process of finding 4,500,000 Summation |
|
10 |
|||
|
18. |
|
M1 A1 M1 M1 A1 M1 A1 M1 M1 A1 |
π cals = 3.76. 99 π = 3.142 = 377.04 Follow through. Follow through. Expressions for the two volumes. Subtraction Expression for the 2 Volume Subtraction π cal = 477.52 π = 3.142 = 477.584 |
|
10 |
|||
|
19. |
|
B1 B1 B1 M1 M1 A1 M1 M1 A1 |
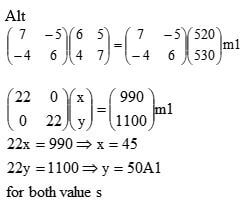
10/100 x 45 x 240 + 13/100 x50 x 100 |
|
10 |
|||
|
20. |
|
B1
B1 B1 B1 B1 B1 B1 M1 M1 A1 |
Location of point Q Location of point R Location of point S. Distance of R from P Bearing of R from P Distance of P from S Bearing of P from S |
|
10 |
|||
|
21. |
|
B1 M1 A1 M1 M1 M1 A1 B1 M1 A1 |
|
|
10 |
|||
|
22. |
|
B1 B1 B1 B1 B1 B2 B1 B1 B1 |
Diagram Diagram Coordinates (Line y – x = 0 can be implied Accept 900 clockwise |
|
10 |
|||
|
22. 23. |
|
B1 B1 B1 B1 M1 A1 B1 B1 M1 A1 |
f column x column fx column √ exp. For x Median class For 250 – 170 Expression |
|
10 |
|||
|
24. |
|
||
|
10 |
Download Mathematics P1 Questions and Answers - Mangu High School Trial Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students