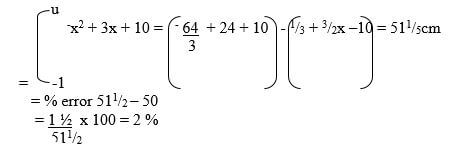INSTRUCTIONS TO CANDIDATES
- Write your name and index number in the spaces provided above.
- Sign and write date of examination in the spaces provided above.
- This paper consists of two sections; Section I and Section II.
- Answer All questions in Section I and only Five questions from section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations giving answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Candidates should answer questions in English.
For examiner’s use only.
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |
GRAND TOTAL ________
QUESTIONS
SECTION 1 (50 MARKS)
Attempt all questions.
- Factorise x2 – y2, hence evaluate 32822 - 32722 (3mks)
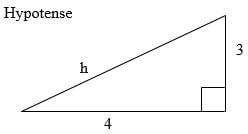
- Find cos x – Sin x, if tan x= ¾ and 90º≤ x ≤360º (3mks)
- Expand [1-2x]6 up to the fourth term. Hence use your expansion to evaluate (1.02)6 to four decimal places. (4mks)
- The average of the first and fourth terms of a GP is 140. Given that the first term is 64. Find the common ratio. (3mks)
- Make b the subject of the formula. (3mks)
A = √ bd
b2 - d - Two variables P and Q are such that P varies partly as Q and partly as the square root of Q. Determine the equation connecting P and Q. When Q=16, P=500 and when Q = 25, P = 800 (4mks)
- Calculate the interest on sh 10,000 invested for 1 ½ years at 12 % p.a. Compounded semi-annually. (3 mks)
- Given that x=2i+j-2k, y= -3i+4j-k and z =5i + 3j+2k and that P= 3x-y+2z, find the magnitude of vector p to 3 significant figure (4mks)
- Eighteen labourers dig a ditch 80m long in 5 days. How long will it take 24 labourers to dig a ditch 64 m long? (3mks).
- The expression 1+ x/2 is taken as an approximation for √1+x. Find the percentage error in doing so if x = 0.44 (3mks)
- The matrices A = [3 0] and B = [a b] are such that AB = A + B Find a, b, and c. (3mks)
[0 4] [0 c] - Simplify (3mks)
2x2 – x-1
x2 – 1 - On map of scale 1:25000 a forest has an area of 20cm2. What is the actual area in Km2 (3mks)
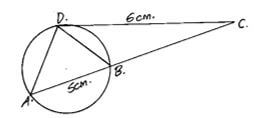
- In the figure below, DC = 6cm, AB = 5cm. Determine BC if DC is a tangent. (3mks).
- Evaluate without using logarithm tables.
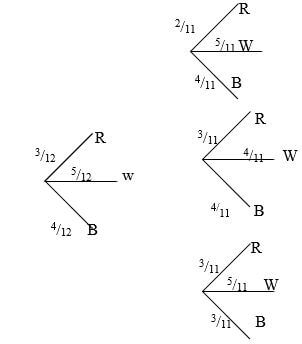
3 log10 2 + log10 750 – log10 6 (3mks) - A bag contains 10 balls of which 3 are red, 5 are white and 2 green. Another bag contains 12 balls of which 4 are red, 3 are white and 5 are green. A bag is chosen at random and a ball picked at random from the bag. Find the probability that the ball so chosen is red. (4mks).
SECTION II (50 MARKS)
Answer any five questions in this section.
- Income tax is charged on annual income at the rates shown below.
Taxable Income K£ Rate (shs per K£)
1 – 1500 2
1501 – 3000 3
3001 – 4500 5
4501 – 6000 7
6001 – 7500 9
7501 – 9000 10
9001 – 12000 12
Over 12000 13
A certain headmaster earns a monthly salary of Ksh. 8570.. He is entitled to tax relief of Kshs. 150 per month.- How much tax does he pay in a year. ( 6 mks)
- From the headmaster’s salary the following deductions are also made every month;
W.C.P.S 2% of gross salary
N.H.I.F Kshs. 1200
House rent, water and furniture charges Kshs. 246 per month.
Calculate the headmaster’s net salary. (4 mks)
-
-
- Taking the radius of the earth, R = 6370 km and π = 22/7 calculate the shorter distance between the two cities P (60ºN , 29ºW) and Q (60ºN, 31ºE) along the parallel of latitude. (3mks)
- If it is 1200Hrs at P, what is the local time at Q. (3mks)
- An aeroplane flew due South from a point A (60ºN, 45ºE) to a point B. The distance covered by the aeroplane was 800km. Determine the position of B. (4mks).
-
- Triangle PQR whose vertices are p(2,2), Q(5,3) and R(4,1) is mapped onto triangle P'Q'R' by a transformation whose matrix is
1 -1
-2 1- On the grid draw PQR and P'Q'R'. (4mks)
- The triangle P'Q'R' is mapped onto triangle P''Q''R'' whose vertices are P''(-2,-2), Q''(-5,-3) and R'' (-4,-1)
- Find the matrix of transformation which maps triangle P'Q'R' onto P''Q''R''.(2mks)
- Draw the image P''Q''R'' on the same grid and describe the transformation that maps PQR onto P''Q''R''. (2mks)
- Find a single matrix of transformation which will map PQR on to P''Q''R''.(2mks)
-
- Complete the table for y = Sin x + 2 Cos x. (2mks)
X
0
30
60
90
120
150
180
210
240
270
300
Sinx
0
1.0
0.5
-0.5
-0.87
2 cos x
2
0
-1.73
-1.73
1.0
Y
2
1.0
-1.23
-2.23
0.13
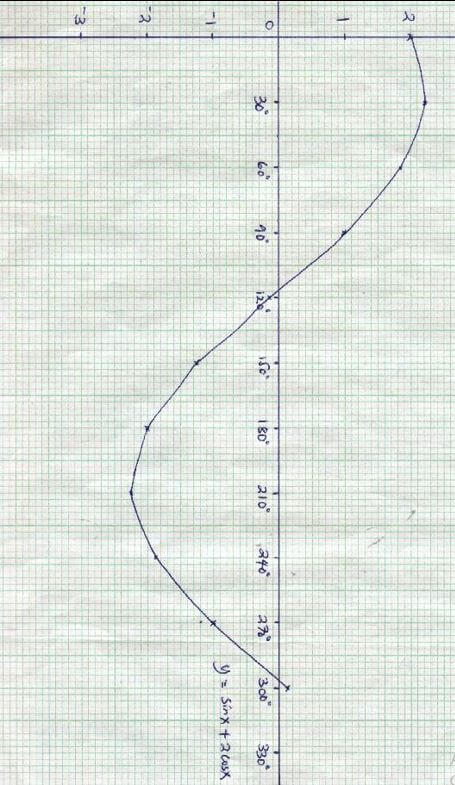
- Draw the graph of y = Sin x + 2 cos x. (3mks)
- Solve sinx + 2 cos x = 0 using the graph. (2mks)
- Find the range of values of x for which y < -0.5 (3mks).
- Complete the table for y = Sin x + 2 Cos x. (2mks)
- A bag contains 3 red, 5 white and 4 blue balls. Two balls are picked without replacement. Determine the probability of picking.
- 2 red balls 2mks
- Only one red ball 2mks
- At least a white ball 2mks
- Balls of same colour. 2mks
- Two white balls 2mks
-
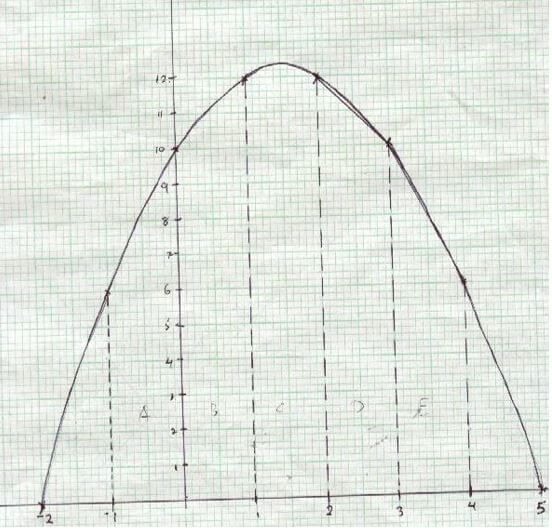
- Draw the graph of the function 2mks
y = 10+3x – x2 for –2≤x≤5 - use of the trapezoidal rule with 5 stripes, find the area under the curve from x = -1 to x = 4. 4mks
- Find the actual area under the curve from x = -1 to x = 4. 2mks
- Find the percentage error introduced by the approximation. 2mks
- Draw the graph of the function 2mks
- The figure below is a cuboid ABCDEFGH such that AB = 8cm, BC = 6cm and CF 5cm.
Determine- the length
- AC (2mks)
- AF (2mks)
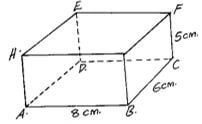
- The angle AF makes with the plane ABCD. (3mks)
- The angle AEFB makes with the base ABCD. (3mks)
- the length
- A manager wishes to hire two types of machine. He considers the following facts.
Machine A Machine B
Floor space 2m2 3m2
Number of men required to operate 4 3
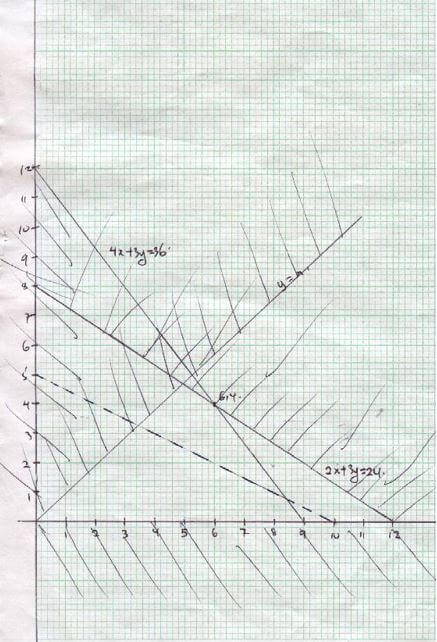
He has a maximum of 24m2 of floor space and a maximum of 36 men available. In addition he is not allowed to hire more machines of type B than of type A.- If he hires x machines of type A and y machines of type B, write down all the inequalities that satisfy the above conditions. 3mks
- Represent the inequalities on the grid and shade the unwanted region. 3mks
- If the profit from machine A is sh. 4 per hour and that from using B is kshs8 per hour. What number of machines of each type should the manager choose to give the maximum profit? (4mks)

MARKING SCHEME
|
1. |
(x- y) ( x+y) |
M1 M1 A1 |
|
|||||||||||||||||||||||||||||||||||
|
|
3 |
|
||||||||||||||||||||||||||||||||||||
|
2. |
Tan x = is positive 3rd quadrant |
B1
M1
A1 |
Identification the hypotenuse
Cao |
|||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||||
|
3. |
16 + 6(- ½ x ) + 15(- ½ x )2 + 20(- ½ x )3 |
M1 M1 M1
A1 |
For simplification
For substitution of x |
|||||||||||||||||||||||||||||||||||
|
|
4 |
|
||||||||||||||||||||||||||||||||||||
|
4. |
a + ar3 = 140 |
M1
M1
A1 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||||
| 5. | a2 = b2d2
b2 –d |
M1 M1 A1 |
sq on both sides | |||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 6 | P = aQ + √Q P = 16a + 4b ( 500 = 16a + 4b) |
M1
M1
M1 A1 |
For equation For formation of simultaneous equations For values of both a and b |
|||||||||||||||||||||||||||||||||||
| 4 | ||||||||||||||||||||||||||||||||||||||
| 7. | 1000 [1 + 6]3 100 1000 x 1.063 ksh 11910.16 11910 |
M1 A1 |
||||||||||||||||||||||||||||||||||||
| 2 | ||||||||||||||||||||||||||||||||||||||
| 8 | 4.562 x 0.38 = 1.73356 4 √1.73356 = 1.14745 ÷ 0.82 = 1.3993 = 1.4 |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 9. | 18 x 64 x 5 24 x 80 6 x 64 8x 16 3 days |
M1 M1 A1 |
For simplification | |||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 10 | True value = √1 + n = 1.44 = 1.2 Approx. value 1 + n = 1 + 44 = 1.22 2 2 = 1.22 – 1.2 = 0.02 0.02 x 100 = 1.2 = 1.67 % |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 11 | [3 0] [a b] = [3 + a b] [0 4] [0 c] [0 4 + c] 3a + 0 = 3 + a 3b + 0 = b 3a = 3 + a → a = 3 2 3b + 0 = b 2b = 0 B = 0 C= 4 |
M1 M1 A1 |
For matrix equation For forming of simultaneous equation For values of a, b and c ( correct) |
|||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 12. | 2x2 – 2x + x -1 ( x + 1 ( x – 1) 2x ( x – 1 ) + 1 ( x- 1) |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 13. |
1 cm = 25000cm 1cm2 = 0.0625 |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 14 |
AB . BC = DC -2 |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 15. |
Log108 + Log10750 - Log106 |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||
| 16. |
P (R )= ½ x 4 |
M1 M1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 4 | ||||||||||||||||||||||||||||||||||||||
| 17. | Taxable income 115 x 8570 = 9855.50 100 9855.50 x 12 p.a 20 5913.30 Tax |
M1 A1 M1 M1 M1 A1 M1 A1 M1 A1 |
||||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 18. |
b) θ x 2πR = 800 |
M1 A1 B1 M1 M1 A1 B1 |
||||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 19. | ||||||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 20 |
|
B2 S1 P1 C1 B2 L1 B2 |
For all 6 values of y Points identified and stated B1 only stated |
|||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 21. |
|
B2 M1 A1 M1 A1 M1 A1 M1 A1 |
prob tree Or equivalent 0.04545 Or equivalent 0.4091 Or equivalent 0.6364 Or equivalent 0.2424 |
|||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 22. |
½ ( 6 + 10 ) + ½ ( 12 + 12) + ½ ( 12 + 10 ) + ½ ( 10 + 6) |
B2 S1 P1 C1 M1 A1 M1 M1 M1 A1 |
8 values B1 at least 6 Appropriate scale use plotting curve |
|||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 23 |
|
M1 A1 M1 A1 B1 M1 A1 B1 M1 A1 |
Sketch Sketch |
|||||||||||||||||||||||||||||||||||
| 10 | ||||||||||||||||||||||||||||||||||||||
| 24. |
Inequalities P profit function object we function Max profit at point (6,4) Hence he should here 6 medium of type A and 4 machine of type B |
|
B1 B1 B1 B1 B1 B1 |
|||||||||||||||||||||||||||||||||||
| 10 |
Download Mathematics P2 Questions and Answers - Mangu High School Trial Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students