Instructions to candidates:
- Write your name, Index number, in the spaces provided above.
- Sign and write the date of examination in the spaces provided above.
- The paper contains two sections: Section I and Section II.
- Answer All the questions in Section I and only five questions from Section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Non – programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
- Candidates should answer the questions in English.
For Examiner’s Use Only
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |
|
|
|
|
|
|
|
|
|

QUESTIONS
SECTION I (50MARKS)
Answer ALL the questions in this section in the spaces provided.
- Use logarithm tables to evaluate
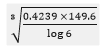 (3 marks)
(3 marks) - Without using a calculator or mathematical table evaluate
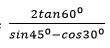 leaving your answer in simplified form. (3 marks)
leaving your answer in simplified form. (3 marks) - Expand
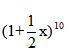 up to the term in x in ascending powers of x3 .Hence find the value of (1.005)10 correct to four decimal places. (3 marks)
up to the term in x in ascending powers of x3 .Hence find the value of (1.005)10 correct to four decimal places. (3 marks) - Solve for x in the equation
2log10x +log105 = 1 + 2log104 (3marks) - In the figure below OS is the radius of a circle centre O. Chords SQ and TU are extended to meet at P and OR is perpendicular to QS at R. OS = 61 cm, PU = 50 cm, UT = 40 and PQ = 30cm.
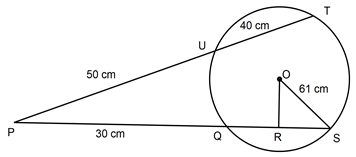
Calculate the length of- QS (2 marks)
- OR to 2 decimal places (2 mark)
- Simplify as far as possible leaving your answer in surd form (3marks)
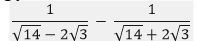
- In the figure below angle A=68º, B= 39º, BC= 8.4cm and CN is the bisector of angle ACB. Calculate the length CN to 1decimal place. (3 marks)
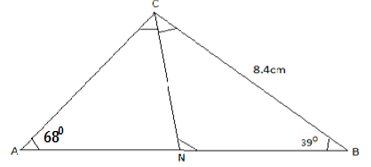
- Given that the matrix
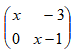 is a singular matrix, find the values of x. (3marks)
is a singular matrix, find the values of x. (3marks) - Make x the subject of the equation (3 marks)
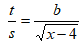
- The equation of the circle is given by x2 + y2 + 8x -2y -1 = 0 . Determine the radius and the centre of the circle. (4marks)
- A coffee blender mixes 6 parts of type A with 4 parts of type B. if type A cost him sh. 24 per kg and type B cost him sh. 22 per kg, at what price per kg should he sell the mixture in order to make 5% profit. Give your answer to 2 decimal places (3marks)
- Musau invested a sum of money which earned him 10% compound interest in the first year. In the second year, the investment earned him 20% compound interest and in the third year, it earned him 25% compound interest. At the end of the three years, the investment was worth sh. 11,550,000. What sum did he invest. (3marks)
- Line AB is 8cm long. On the same side of line AB draw the locus of point P such that the area of triangle APB is 12cm2 and angle APB=90º (3marks)
- In a class of 20 students, there are 12 boys and 8 girls. If two students from the class are chosen at random to go to trip, what is the probability that both of them are boys (3marks)
- After transformation T represented by the matrix (2 1), the triangle ABC was mapped onto triangle A1B1C1 where A1,B1,C1had coordinates (2,0), (4,0) and (4,6) respectively. Determine the coordinates A, B, and C (3marks)
- The length and breadth of a rectangular floor were measured and found to be 4.1m and 2.2m respectively. If a possible error of 0.01m was made in each of the measurements; find the:
- Maximum and minimum possible area of the floor (2marks)
- Maximum wastage in the carpet ordered to cover the whole floor. (1mark)
SECTION II (50 MARKS)
INSTRUCTIONS: Answer ANY FIVE questions only in this section
-
- complete the table below, giving the values correct to 2 decimal places (2mks)
X0
00
150
300
450
600
750
900
1050
1200
1350
1500
1650
1800
Cos 2X0
1.00
0.87
0.00
-0.5
-1.00
-0.5
0.00
0.50
0.87
1.00
Sin (X0+300)
0.50
0.71
0.87
0.97
1.00
0.87
0.71
0.50
0.00
-0.50
- Using the grid provided draw on the same axes the graph of y=cos 2Xº and y=sin(Xº+30º) for
0º≤X≤180º. (4mks)
- Find the period of the curve y=cos 2xº (1mk)
- Using the graph, estimate the solutions to the equations;
- sin(Xº+30º)=cos 2Xº (1mk)
- Cos 2Xº=0.5 (1mk)
- complete the table below, giving the values correct to 2 decimal places (2mks)
- A Quantity P varies partly as the square of m and partly as n. When p= 3.8, m = 2 and n = -3, When p = - 0.2, m = 3 and n= 2.
- Find
- The equation that connects p, m and n (4marks)
- The value of p when m = 10 and n = 4 (1mark)
- Express m in terms of p and n (2marks)
- If P and n are each increased by 10%, find the percentage increase in m correct to 2 decimal place. (3marks)
- Find
-
- The 5th term of an AP is 16 and the 12th term is 37.
Find;- The first term and the common difference ( 3 marks)
- The sum of the first 21 terms (2 marks)
- The second, fourth and the seventh term of an AP are the first 3 consecutive terms of a GP. If the common difference of the AP is 2.
Find: - The common ratio of the GP ( 3 marks)
- The sum of the first 8 terms of the GP (2 marks)
- The 5th term of an AP is 16 and the 12th term is 37.
- The table below shows the rates of taxation in a certain year.
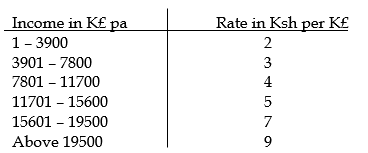
In that period, Juma was earning a basic salary of sh. 21,000 per month. In addition, he was entitled to a house allowance of sh. 9000 p.m. and a personal relief of ksh.1056 p.m He also has an insurance scheme for which he pays a monthly premium of sh. 2000. He is entitled to a relief on premium at 15% of the premium paid.- Calculate how much income tax Juma paid per month. (7mks)
- Juma’s other deductions per month were cooperative society contributions of sh. 2000 and a loan repayment of sh. 2500. Calculate his net salary per month. (3mks)
- A cupboard has 7 white cups and 5 brown ones all identical in size and shape. There was a blackout in the town and Mrs. Kamau had to select three cups, one after the other without replacing the previous one.
- Draw a tree diagram for the information. (2mks)
- Calculate the probability that she chooses.
- Two white cups and one brown cup. (2mks)
- Two brown cups and one white cup. (2mks)
- At least one white cup. (2mks)
- Three cups of the same colour. (2mks)
- The For a sample of 100 bulbs, the time taken for each bulb to burn was recorded. The table below shows the result of the measurements.
Time(in hours)
15-19
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70-74
Number of bulbs
6
10
9
5
7
11
15
13
8
7
5
4
- Using an assumed mean of 42, calculate
- the actual mean of distribution (4mks)
- the standard deviation of the distribution (3mks)
- Calculate the quartile deviation (3mks)
- Using an assumed mean of 42, calculate
- The position of town A and B on the earth’s surface are (36ºN, 49ºE) and (36ºN, 131ºW) respectively.
- Find the difference in longitude between town A and town B (2marks)
- Given that the radius of the earth is 6370km, calculate the distance between town A and B along;
- Parallel of longitude (2marks)
- A great circle (3marks)
- Another town C is 840km east of town B and on the same latitude as town A and B. find the longitude of town C (3marks)
- A trader is required to supply two types of shirts, type A and type B. the total number of shirts must not be more than 400. He has to supply more of type A than type B shirts. However the number of type A shirts must not be more than 300 and the number of type B shirts must not be less than 80. Let x be the number of type A shirts and y be the number of type B shirts.
- Write down in terms of x and y all the linear inequalities representing the information above (4marks)

- On the grid provided, draw the inequalities and shade the unwanted regions (4marks)
- The profits were as follows;
Type A: sh. 600 per shirt
Type B: sh. 400 per shirt- Use the graph to determine the number shirts of each type that he should make to maximize the profit (1mark)
- Calculate the maximum possible profit (1mark)
- Write down in terms of x and y all the linear inequalities representing the information above (4marks)

MARKING SCHEME
SECTION I (50MARKS)
Answer ALL the questions in this section in the spaces provided.
- Use logarithm tables to evaluate
 (3 marks)
(3 marks)
No standard form log 1.19111
3
=0.63700.4239 0.4239 × 10-1 ¯1.6272 149.6 1.496 × 102 2.1750 1.9022 log 6 = 0.7782 7.782 × 10-1 ¯1.8911 1.9111 4.335 4.335 × 100 0.6370 - Without using a calculator or mathematical table evaluate
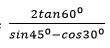 leaving your answer in simplified form. (3 marks)
leaving your answer in simplified form. (3 marks)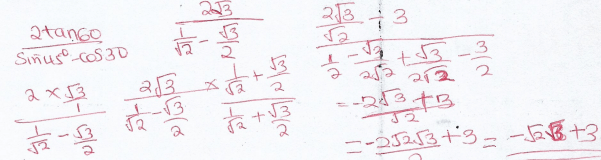
- Expand
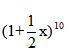 up to the term in x in ascending powers of x3 .Hence find the value of (1.005)10 correct to four decimal places. (3 marks)
up to the term in x in ascending powers of x3 .Hence find the value of (1.005)10 correct to four decimal places. (3 marks)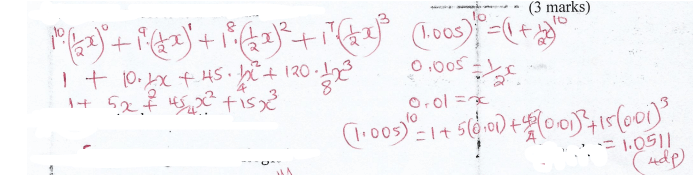
- Solve for x in the equation
5log10x +log105 = 1 + 2log104 (3marks)
5log10x +log105 = 1 + 2log104
log105x5 = log10160
5x5 = 160
x5 = 32
x5 = 25 =
x = 2 - In the figure below OS is the radius of a circle centre O. Chords SQ and TU are extended to meet at P and OR is perpendicular to QS at R. OS = 61 cm, PU = 50 cm, UT = 40 and PQ = 30cm.

Calculate the length of- QS (2 marks)
PT.PU = PS.PQ
90 × 50 = (30 × QS) × 30
4500 = 900 + 30QS
30QS = 3600
QS = 120 - OR to 2 decimal places (2 mark)
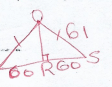
OR = √612 - 602
= √121
= 11.00 cm
- QS (2 marks)
- Simplify as far as possible leaving your answer in surd form (3marks)
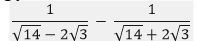
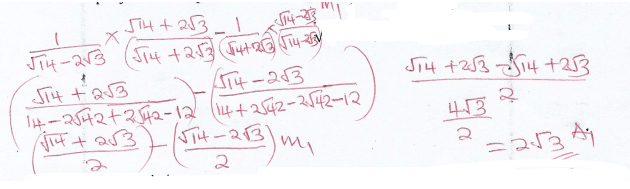
- In the figure below angle A=68º, B= 39º, BC= 8.4cm and CN is the bisector of angle ACB. Calculate the length CN to 1decimal place. (3 marks)

∠ACN = 180 - (68 + 39)
2
=365º
8.4 = x
sin68º sin39º
x = 5.701 cm - Given that the matrix
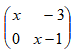 is a singular matrix, find the values of x. (3marks)
is a singular matrix, find the values of x. (3marks)
x (x - 1) - 0 = 0
x = 0
x = 1 - Make x the subject of the equation (3 marks)
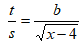
(t)2 = b2
(s) x - 4
t2(x - 4) = s2b2
t2x - 4t = s2b2
t2x = s2b2 + 4t
x = s2b2 + 4t
t2 - The equation of the circle is given by x2 + y2 + 8x -2y -1 = 0 . Determine the radius and the centre of the circle. (4marks)
x2 + 8x + 16 + y2 - 2y + 1 = 1 + 16 + 1
(x + 4)2 + (y - 1)2 = 18
center x(-4,1)
radius = √18 = 4.243 units
or
r = 3√2 units - A coffee blender mixes 6 parts of type A with 4 parts of type B. if type A cost him sh. 24 per kg and type B cost him sh. 22 per kg, at what price per kg should he sell the mixture in order to make 5% profit. Give your answer to 2 decimal places (3marks)
avearage cost = total cost
total
=(24 × 6) + (22 × 4)
6 + 4
144 + 88 = 222 = 23.2
10 10
105 × 23.2 = 24.35
100 - Musau invested a sum of money which earned him 10% compound interest in the first year. In the second year, the investment earned him 20% compound interest and in the third year, it earned him 25% compound interest. At the end of the three years, the investment was worth sh. 11,550,000. What sum did he invest. (3marks)
1st year
A = P(1 + r )n
100
A = P(1 + 10 )1
100
A = 1.1P
2nd year
A = 1.1P(1 + 20 )1
100
= 1.1P(1 + 0.2)
A = 1.1P × 1.2
A = 1.32P
3rd year
A = 1.32P(1 + 25 )1
100
= 1.65P = 1150000
P = sh 7 000 000 - Line AB is 8cm long. On the same side of line AB draw the locus of point P such that the area of triangle APB is 12cm2 and angle APB=90º (3marks)
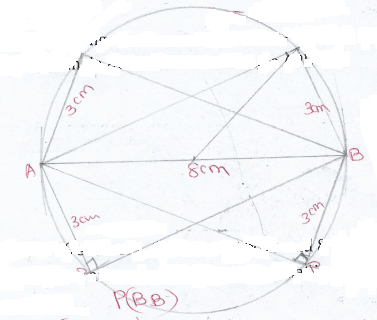
p is a point substended by chord AB to the circumference of a semi-circle or circle - In a class of 20 students, there are 12 boys and 8 girls. If two students from the class are chosen at random to go to trip, what is the probability that both of them are boys (3marks)
( 12 × 11) = 132 = 33
20 19 380 95 - After transformation T represented by the matrix (2 1), the triangle ABC was mapped onto triangle A1B1C1 where A1,B1,C1had coordinates (2,0), (4,0) and (4,6) respectively. Determine the coordinates A, B, and C (3marks)
A B C A B C
(2 1) ( x1 x2 x3) = (2 4 4)
(0 1) (y1 y2 y3) (0 0 6)
2x1 + y1 = 2
0 + y1 = 0
y1 = 0
x1 = 1
2x2 + y2 = 4
0 + y2 = 0
y2 = 0
x2 = 2
2x3 + y3 = 4
0 + y3 = 6
y3 = 6
2x3 = -2
x3 = -1
A(1,0)
B(2,0)
C(-1,6) - The length and breadth of a rectangular floor were measured and found to be 4.1m and 2.2m respectively. If a possible error of 0.01m was made in each of the measurements; find the:
- Maximum and minimum possible area of the floor (2marks)
maximum area = 4.11 m × 2.21m = 9.0831m2
minimum area = 4.09m × 2.19m = 8.9571m2 - Maximum wastage in the carpet ordered to cover the whole floor. (1mark)
actual area = 4.1 ×2.2
=9.022
wastage = (9.02 - 8.9571) + (9.0831 - 9.02)
2
= 0.063
- Maximum and minimum possible area of the floor (2marks)
SECTION II (50 MARKS)
INSTRUCTIONS: Answer ANY FIVE questions only in this section
-
- complete the table below, giving the values correct to 2 decimal places (2mks)
X0
00
150
300
450
600
750
900
1050
1200
1350
1500
1650
1800
Cos 2X0
1.00
0.87
0.50
0.00
-0.5
-0.87
-1.00
-0.87
-0.5
0.00
0.50
0.87
1.00
Sin (X0+300)
0.50
0.71
0.87
0.97
1.00
0.97
0.87
0.71
0.50
0.26
0.00
-0.26
-0.50
- Using the grid provided draw on the same axes the graph of y=cos 2Xº and y=sin(Xº+30º) for
0º≤X≤180º. (4mks)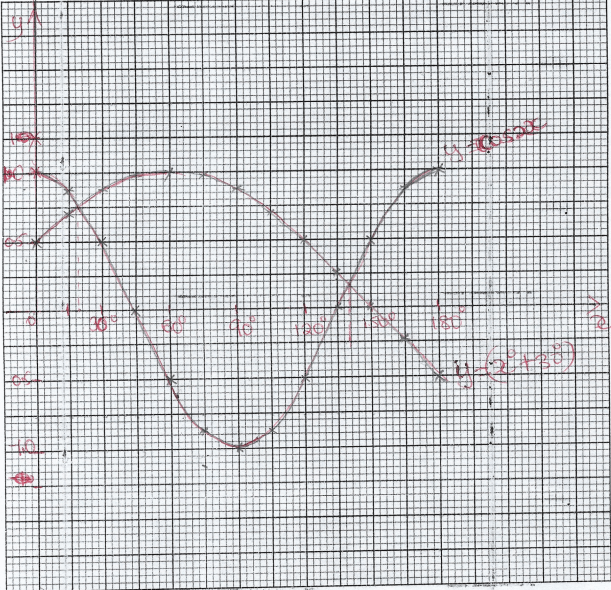
- Find the period of the curve y=cos 2xº (1mk)
360
b
= 360 = 180º
2 - Using the graph, estimate the solutions to the equations;
- sin(Xº+30º)=cos 2Xº (1mk)
x = 18.5 ± 2º
x = 139º ± 2º - Cos 2Xº=0.5 (1mk)
x= 30º
- sin(Xº+30º)=cos 2Xº (1mk)
- complete the table below, giving the values correct to 2 decimal places (2mks)
- A Quantity P varies partly as the square of m and partly as n. When p= 3.8, m = 2 and n = -3, When p = - 0.2, m = 3 and n= 2.
- Find
- The equation that connects p, m and n (4marks)
p = xm2 + yn
3.8 = 4x - 3y
-0.2 = 9x + 2y
7.6 = 8x - 6y
- 0.6 = 27x + 6y +
7 35x
7 = x
35
x = 1/5 = 0.2
3.8 = 0.8 - 3y
-1 = y
p = 0.2m2 - n - The value of p when m = 10 and n = 4 (1mark)
p = 0.2m2 - n
p = 20 - 4
p = 16
- The equation that connects p, m and n (4marks)
- Express m in terms of p and n (2marks)
p = 0.2m2 - n
0.2m2 = p + n
m2 = p + n
0.2
m = √p + n
0.2
m = ± √p + n
0.2 - If P and n are each increased by 10%, find the percentage increase in m correct to 2 decimal place. (3marks)
m0 = √p + n
0.2
m1 = √1.1(p + n)
0.2
m1 = √1.1p + 1.1n = √5.5(p + n)
0.2
= 2.3452√(p + n)
m0 = √p + n = √5(p + n)
0.2
= 2.2361√(p + n)
% change in m = (m1 - m0) × 100%
m0
= 2.3452√(p + n) - 2.2361√(p + n)
2.2361√(p + n)
= 2.3452- 2.2361 × 100%
2.2361
= 0.1001 × 100%
2.2361
= 0.04879 × 100%
= 4.88% 2dp
- Find
-
- The 5th term of an AP is 16 and the 12th term is 37.
Find;- The first term and the common difference ( 3 marks)
Tn = a + (n - 1)d
T5 = a + 4d = 16
T2 = a + 11d = 37
-7d = -21
d = 3
a + 4(3) = 16
a + 12 = 16
a = 4 - The sum of the first 21 terms (2 marks)
Sn = n/2(2a + (n - 1)d)
=21/2((2 × 4) + (20 × 3))
= 714
- The first term and the common difference ( 3 marks)
- The second, fourth and the seventh term of an AP are the first 3 consecutive terms of a GP. If the common difference of the AP is 2.
Find: - The common ratio of the GP ( 3 marks)
a + d, a + 3d, a + 6d
a + 2, a + 6, a + 12
a + 6 = a + 12
a + 2 a + 6
(a + 6)2 = (a + 2) (a + 12)
a2 + 12a + 36 = a2 + 14a + 24
2a = 12
a = 6
G.p
8, 12, 18
r = 12
8
= 1½ - The sum of the first 8 terms of the GP (2 marks)
S8 = 8 ((3/2)8 - 1)
1½ - 1
= 394.0625
- The 5th term of an AP is 16 and the 12th term is 37.
- The table below shows the rates of taxation in a certain year.

In that period, Juma was earning a basic salary of sh. 21,000 per month. In addition, he was entitled to a house allowance of sh. 9000 p.m. and a personal relief of ksh.1056 p.m He also has an insurance scheme for which he pays a monthly premium of sh. 2000. He is entitled to a relief on premium at 15% of the premium paid.- Calculate how much income tax Juma paid per month. (7mks)
taxable income = 21000 + 9000
= sh.30,000
p.a. = 30,000 × 12 = k.f 18,000 p.a.
20
2 × 3900 = sh. 7800
3 × 3900 =sh.11700
4 × 3900 = sh.15600
5 × 3900 = sh.19500
7 × 2400 = sh.16800
sh.71400
tax paid = 71400 - 16272
= sh 55128
P.A.Y.E = 55128
12
= sh. 4594
15 × 2000 = 300
100
total relief p.a. = (300 + 1056) × 12 = sh. 16272 - Juma’s other deductions per month were cooperative society contributions of sh. 2000 and a loan repayment of sh. 2500. Calculate his net salary per month. (3mks)
total deductions = 4594 + 2000 + 2000 + 2500
sh 11094 per month
net salary = 30000 - 11094
=sh 18,906.00
- Calculate how much income tax Juma paid per month. (7mks)
- A cupboard has 7 white cups and 5 brown ones all identical in size and shape. There was a blackout in the town and Mrs. Kamau had to select three cups, one after the other without replacing the previous one.
- Draw a tree diagram for the information. (2mks)
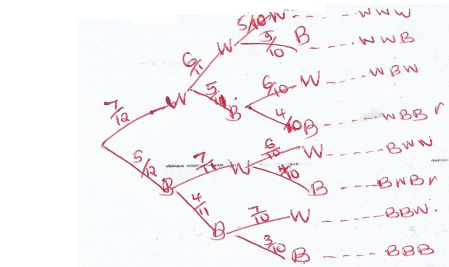
- Calculate the probability that she chooses.
- Two white cups and one brown cup. (2mks)
(7 × 6 × 5) + (7 × 5 × 6) + (5 × 7 × 6)
12 11 10 12 11 10 12 11 10
= 21
44 - Two brown cups and one white cup. (2mks)
(7 × 5 × 4) + (5× 7 × 4) + (5 × 4 × 7)
12 11 10 12 11 10 12 11 10
= 7
22 - At least one white cup. (2mks)
(5 × 4 × 5) + (5× 7 × 4) + (7 × 5 × 4) + (5 × 7 × 6) + (7 × 5 × 6) + (7 × 6 × 5) + (7 × 6 × 5)
12 11 10 12 11 10 12 11 10 12 11 10 12 11 10 12 11 10 12 11 10
= 427
440 - Three cups of the same colour. (2mks)
(7 × 6 × 5) + (5 × 4 × 3)
12 11 10 12 11 10
= 9
44
- Two white cups and one brown cup. (2mks)
- Draw a tree diagram for the information. (2mks)
- The For a sample of 100 bulbs, the time taken for each bulb to burn was recorded. The table below shows the result of the measurements.
Time(in hours)
15-19
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70-74
Number of bulbs
6
10
9
5
7
11
15
13
8
7
5
4
- Using an assumed mean of 42, calculate
- the actual mean of distribution (4mks)

- the standard deviation of the distribution (3mks)
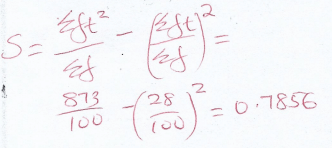
- the actual mean of distribution (4mks)
- Calculate the quartile deviation (3mks)
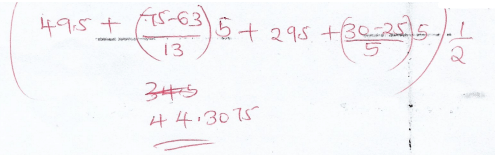
- Using an assumed mean of 42, calculate
- The position of town A and B on the earth’s surface are (36ºN, 49ºE) and (36ºN, 131ºW) respectively.
- Find the difference in longitude between town A and town B (2marks)
A(36ºN, 49ºE) B(36ºN, 131ºW)
longitudinal difference
49º + 131º = 180º - Given that the radius of the earth is 6370km, calculate the distance between town A and B along;
- Parallel of longitude (2marks)
Distance = 2πRcosθ
360 × 22 × 6370 cos36
dist = 16196.52023km - A great circle (3marks)
dist = σ2πR
360
= 108 × 2 × 22 × 6370
360 7
dist = 12,012km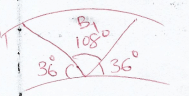
- Parallel of longitude (2marks)
- Another town C is 840km east of town B and on the same latitude as town A and B. find the longitude of town C (3marks)
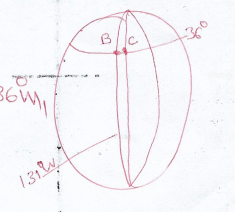
B(36º, 131ºw)
D = σ2πRcosσ
360
840 = σ × 2 × 22 × 6370cos 36º
360 7
840 = 89.9807σ
9.34º = σ
131º - 9.34º = 121.66º
longitude of town c = 121.66ºw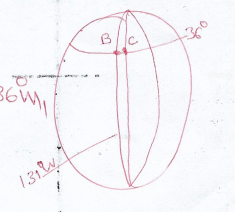
- Find the difference in longitude between town A and town B (2marks)
- A trader is required to supply two types of shirts, type A and type B. the total number of shirts must not be more than 400. He has to supply more of type A than type B shirts. However the number of type A shirts must not be more than 300 and the number of type B shirts must not be less than 80. Let x be the number of type A shirts and y be the number of type B shirts.
- Write down in terms of x and y all the linear inequalities representing the information above (4marks)
x + y ≤ 400
x ≤ y
x > 0
x ≤ 300
y ≥ 80
y > 0
- On the grid provided, draw the inequalities and shade the unwanted regions (4marks)
- The profits were as follows;
Type A: sh. 600 per shirt
Type B: sh. 400 per shirt- Use the graph to determine the number shirts of each type that he should make to maximize the profit (1mark)
sample
(150, 200)
(200, 200)
(180,220)
(150,250)
(100,300)
200 type A
200 type B - Calculate the maximum possible profit (1mark)
600A + 4000p = max profits
(600 × 200) + (400 × 200)
120000 + 80000
=sh. 20000
- Use the graph to determine the number shirts of each type that he should make to maximize the profit (1mark)
- Write down in terms of x and y all the linear inequalities representing the information above (4marks)
Download Mathematics P2 Questions and Answers - Nambale Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

