INSTRUCTIONS TO CANDIDATES
- Mathematical tables and non-programmable calculators may be used.
- This paper consists of section A and section B.
- Attempt all the questions in the spaces provided.
- ALL working MUST be clearly shown.
QUESTION 1
You are provided with the following apparatus
- Ammeter
- A voltmeter
- A wire mounted on a millimeter scale
- A switch
- A new dry cell
- A micrometer screw gauge
- 6 Connecting wires
- A jockey
Proceed as follows
- Measure the diameter d of the mounted wire at three different points
d1= ____________________________________ mm
d2=____________________________________ mm (½mk)
d3=____________________________________ mm
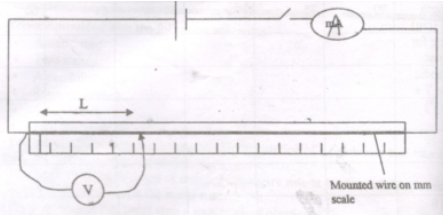
Average d = ____________________________________ mm (½mk) - Set up the apparatus as shown in the circuit diagram.
Close the switch and tap the mounted wire with jockey as shown in the circuit. Ensure that both meters show positive deflection, open the switch. - Tap the wire at L= 20cm, close the switch, read and record in the table the ammeter and voltmeter reading.
- Repeat the procedure in (c) for other values of L shown in the table and complete the table.
(6mks)L(m) V(Volts) I(A) R= V/I 0.2 0.3 0.4 0.5 0.6 0.7 0.8 - Plot a graph of R against L (m). (5mks)
- Determine the slope of the graph. (3mks)
- Given that R= pL/A where A is the cross-sectional area of the wire and p is a constant for the material of the wire, determine the value of the constant p. (3mks)
QUESTION 2
Part I
You are provided with the following;
- A spiral spring
- A complete stand
- 7 masses of 20g each
- A stop watch
- 2 small pieces of wood for clamping
Proceed as follows
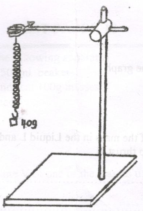
- Clamp the spiral spring so as to hang from the clamp as shown in the figure below
- Hang a 40g mass from the spring and displace the mass slightly downwards so that it executes vertical oscillations as shown
- Measure and record in the table the time for 10 oscillations.
- Determine the periodic time T in the table.
- Repeat the experiment for other values of mass m shown in the table. Complete the table below.
Mass (m)g 40 60 80 100 120 140 Mass m (kg) Time for 10 osc(s) Period T(s) T2 (s2) - Plot a graph of T2 (s2) against mass m(kg). (5mks)
- Determine the slope of the graph. (2mks)
- Given that the equation of the graph is T2 = 4π²m
w
Determine the value of w. (3mks)
Part II
You are provided with a glass block, 4 optical pins, a soft board, one plain paper.
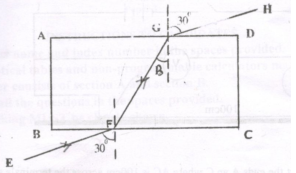
- Place the rectangular glass block on a sheet of paper fixed on the soft board with one of its longest face uppermost. Mark the outline ABCD as shown in the figure. Remove the glass block and draw a line EF to represent a ray of light making an angle of incidence i=30° with the longest side BC of the block.
- Stand pins p1and p2 on this line as far as possible. Replace the block and mark the emergent ray by looking into the side AD of the block and placing pins p3 and p4 in line with images of p1 and p2 as seen through the glass block. Remove the block and the pins and draw ray EFGH as shown in the figure below.
- Draw the normal at G as shown.
- Measure angle B (1mk)
B = …………………………………………………………… - Given that k = sin 30°
sin B
Calculate the value of k. (2mks) - The main paper used should be handed over together with this paper (correct use made of the plain paper) (1mk)
CONFIDENTIAL
QUESTION ONE REQUIREMENTS
- Ammeter
- Voltmeter
- Nichrome wire mounted on a millimeter scale (gauge 28)
- Switch
- A new dry cell
- A micrometer screw gauge
- Connecting wires
- A jockey
QUESTION TWO REQUIREMENTS
- A spiral spring (spring diameter =15mm
Length= 70mm, diameter of spring wire=1.8mm, number of turns=88) - A complete stand
- 7 masses of 20g each
- A stopwatch
- 2 small pieces of wood for clamping
- A glass block
- 4 optical pins
- A soft board
- One plain paper
- Student to come with geometrical set.

MARKING SCHEME
Question 1
- d1= 0.38mm
d2=0.39 mm
d3= 0.40 mm (½mk)
Average d = 0.38+0.39+0.40
3
= 0.39 ± 0.02mm (½mk) -
Length (m) V(volt) I(A) R= V/t 0.2
0.3
0.4
0.5
0.6
0.7
0.80.30
0.40
0.50
0.60
0.70
0.90
1.00
±0.05
(2mks)0.10
0.10
0.10
0.10
0.10
0.10
0.10
±0.05
(2mks)All correct ot four significant or exact
(2mks)- axes labeled with units (1mk)
- Uniform and simple scale (1mk)
- correct plotting within one small square
(4pts x ½mk= 2mks) - Straight line with a positive gradient passing at least three points. (1mk)
-
- Correct interval within one small square (1mk)
- Correct substitution and evaluation (1mk)
- Answer accuracy with units (1mk)
-
- Slope = P/A area to be in SI unit.
- Correct calculation of cross sectional area of the wire, A = п (d/2) 2 (1mk)
- P= slope x A; correct substitution and evaluation. (1mk)
- Answer accuracy with unit. (1mk)
Question 2
Part 1
(e) Table
| Mass (m)g | 40 | 60 | 80 | 100 | 120 | 140 |
| Mass m (kg) | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 |
| Time for 10 osc(s) | 3.85 | 3.90 | 4.50 | 5.22 | 5.60 | 6.03 |
| Period T(s) | All correct to 4s.f or exact | |||||
| T2 (s2) | All correct to 4s.f or exact | |||||
(f)
- Axes labeled with units (1mk)
- Uniform and simple scale (1mk)
- Correct plotting within one small square (4pts x ½mk= 2mks)
- Straight line with a positive gradient passing through at least 3 points. (1mk)
(g)
- Correct interval within one small square. (½mk)
- Correct substitution and evaluation (½mk)
- Answer accuracy with units (1mk)
(h)
- Form y= mx+c
Slope = 4π²
w - Correct substitution (1mk)
- Correct evaluation (1mk)
- Answer accuracy with units (1mk)
PART II
(c) Angle B = 18° ±1° (1mk)
(d)
- Correct substitution (1mk)
- Correct evaluation and answer (1mk)
- Correct use of the plain paper (1mk)
Download Physics Paper 3 Questions and Answers with Confidential - Bungoma Diocese Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students