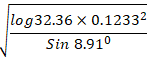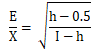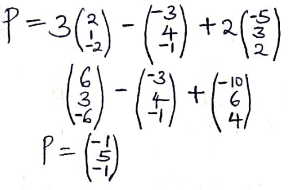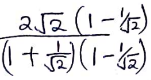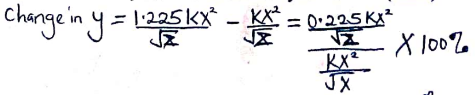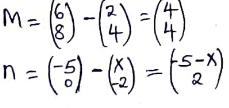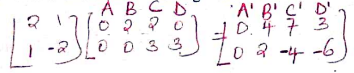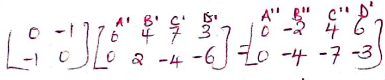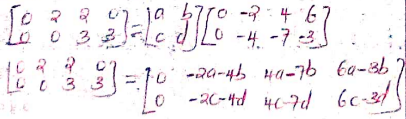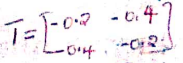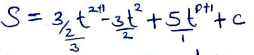INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections: Section I and Section II.
- Answer ALL questions in section 1 and ONLY FIVE questions from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
SECTION I
Answer all questions in the spaces provided.
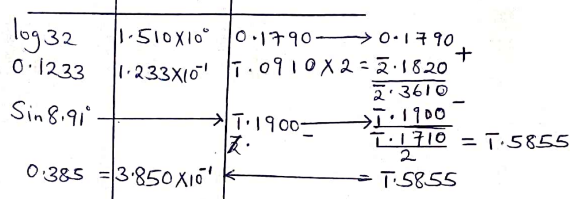
- Using logarithm tables evaluate. (4mks)
- A circle which passes through the point (-1, 7) has its center at (3, -3). Determine the equation of the circle in the form. x2 + y2 + ax + by + c = 0 Where a, b and c are constants. (3 mks)
- Expand (1 + 2x)7 up to the term in x3. Use your expansion to estimate (1.02)7 to 4dp (3mks)
- Solve 1 + 2 sin 2x = 0 for 0° ≤ 360°.(3 mks)
- Given that x = 2i +j – 2k, y =-3i + 4j – k and z = -5i + 3j + 2k and that p = 3x – y + 2z,
Calculate the magnitude of p correct to 3 significant figures. (3 mks) - Calculate the semi interquartile range for the following set of data. (4 mks)
16, 42, 41, 6, 20, 28, 19, 23, 15 - Make h the subject of the formula (3 mks)
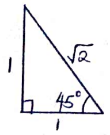
- Evaluate by rationalizing the denominator and leaving your answer in surd form. (3 mks)
√8
1+Cos45° - A dealer has two types of grades of tea, A and B. Grade A costs sh140 per kg. Grade B costs sh. 160 per kg. If the dealer mixes A and B in the ratio 3:5 to make a brand of tea which he sells at sh. 180 per kg, calculate the percentage profit that he makes. (3 mks)
- Onyango bought a refrigerator whose cash price is Sh.84,000 on hire purchase. He made a cash deposit of sh. 20,000 and the 15 monthly instalments of Sh. 6,000. Calculate the rate of interest per month. (3 mks)
- Estimate the area bounded by the curve y = ½x2 + 1, x = 0, x = 3 and the x-axis using the mid-ordinate rule. Use three strips (3 mks)
- A variable y varies as the square of x and inversely as the square root of z. Find the percentage change in y when x is increased by 5% and z reduced by 19%. (3mks)
- A two digit number is such that the sum of ones and tens digit is ten. If the digits are reversed, the new number formed exceeds the original number by 54.Find the original number. (3mks)
- The current price of a vehicle is Sh500 000.If the vehicle depreciates at a rate of 15% p.a., find the number of year it will take for its value to fall to Sh180 000. (3mks)
- The gradient function of a curve at any point (x, y) is given as 6x2 .Given that the curve passes through the point (1, 5), find its equation. (3mks)
- Vector m passes through the points (6, 8) and (2, 4).Vector n passes through (x, -2) and (-5, 0), if m is parallel to n determine the value of x. (3mks)
SECTION II
Answer any FIVE questions from this section
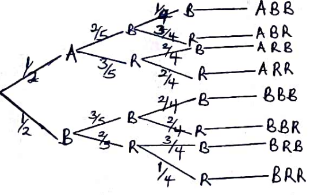
- Two bags A and B contain red and blue balls. Bag A contains 2 blue balls and 3 red balls while bag B contains 3 blue balls and 2 red balls. A bag is selected at random and two balls picked without replacement.
- Use a tree diagram to illustrate the above information (2mks)
- Use the tree diagram above to find the probability of picking
- Balls of the same colour (2mks)
- A red ball followed by a blue ball (2mks)
- At least a blue ball (2mks)
- One red ball (2mks)
- The 2nd and the 5th terms of an arithmetic progression are 8 and 17 respectively, the 2nd, 10th and the 42nd terms of the A.P form the first three terms of a geometric progression. Find.
- The 1st term and the common difference of the A.P. (3mks)
- The first three terms of G.P and the 10th term of the G.P. (4mks)
- The sum of the first 10 terms of the G.P. (3mks)
-
Height in cm 1-5 6-10 11-15 16-20 21-25 26-30 31-35 36-40 41-45 46-50 Number of plants 1 3 5 6 7 7 7 7 5 2 - Draw a cumulative frequency curve on the grid provide to represent the data above. (4 mks)
- From the graph, determine:
- The median height (2mks)
- The quartile deviation (2mks)
- The range of the height of the middle 50% of the plants. (2 mks)
-
- Complete the table below for the function y = 3x2 – 2x – 1 for -3 ≤ x ≤ 4. (3 mks)
X −3 −2 −1 0 1 2 3 4 3x2 3 27 −2x 6 −8 −1 Y 15 7 - Draw the graph of y = 3x2 – 2x – 1. (4 mks)
- Draw the line y =3x + 1 on the same axis hence find the values of x for which y = 3x + 1 and y = 3x2 – 2x – 1 are equal. (3 mks)
- Complete the table below for the function y = 3x2 – 2x – 1 for -3 ≤ x ≤ 4. (3 mks)
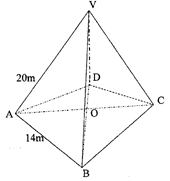
- The diagram below shows a right pyramid with a square base ABCD and vertex V. O is the centre of the base. AB = 14m, VA = 20m and N is the midpoint of BC.
Find;- The lengths of BO, VO and VN (3 mks)
- The angle between VO and plane VBC (3 mks)
- The angle between VB and base ABCD (2 mks)
- The volume of the pyramid VABCD (2 mks)
- A transformation represented by matrix
maps A(0,0), B(2,0), C(2,3) and D(0,3) onto A1B1C1 and D1 respectively.
- Draw ABCD and its image A¹B¹C¹D¹ (4 mks)
- A transformation represented by
maps A¹B¹C¹D¹ on A¹¹B¹¹C¹¹D¹¹. Plot A¹¹B¹¹C¹¹D¹¹on the same graph.
(3 mks) - Determine the matrix of a single transformation that maps A¹¹B¹¹C¹¹D¹¹onto ABCD (3 mks)
-
- The acceleration of a particle t seconds after passing a fixed point P is given by a = 3t – 3. Given that the velocity of the particle when t = 2 is 5 m/s, find;
- Its velocity when t = 4 seconds (3 mks)
- Its displacement at this time (3 mks)
- Find the exact area bounded by the graph x = 9y – y3 and the y-axis (4 mks)
- The acceleration of a particle t seconds after passing a fixed point P is given by a = 3t – 3. Given that the velocity of the particle when t = 2 is 5 m/s, find;
- The position of 3 cities P, Q and R are (15°N, 20°W) (50°N, 20°W) and (50°N, 60°E) respectively.
- Find the distance in nautical miles between:
- Cities P and Q (2 mks)
- Cities P and R, via city Q (3 mks)
- A plane left city P at 0250h and flew to city Q where it stopped for 3 hours then flew on to city R, maintaining a ground speed of 900 knots throughout. Find:
- The local time city R when the plane left city P (3 mks)
- The local time (to the nearest minute) at city R when the plane landed at R. (2 mks)
- Find the distance in nautical miles between:

MARKING SCHEME
-
-
r = √(16+100) = √116
r2 = 116
(x − 3)2 + (y + 3)2 = 116\
x2 − 6x + 9 +y2 + 6y + 9 − 116 = 0
x2 + y2− 6x + 6y − 98 = 0 -
1 + 14x + 84x2 + 280x3
2x = 0.02
x = 0.01
1 + 14(0.01) + 84(0.01)2 + 280(0.01)3
=1.1487 - 2 sin 2x = −1
sin 2x = −½
2x = 210°, 330°, 570°, 690°
x = 105°, 165°, 285°, 345° -
IPI = √((−1)2 + (5)2 + (−1)2
=5.20 units - 6, 15, 16, 19, 20, 23, 28, 41, 42
Q1 = 15+16 = 15.5
2
Q3 = 28+41 = 34.5
2
34.5 − 15.5 = 9.5
2 - E² = h − 0.5
X² 1 − h
E² − E²h = X²h − 0.5X²
E² + 0.5X² = X²h + E²h
h(X² + E²) = E² + 0.5X2
h = E² + 0.5X²
X² + E² -
Cos 45° = 1/√2
2√2 − 2
1 −½
2√2 − 2
½
4√2 − 4 - (140 × 3) + (160 × 5) = Sh 152.50
8
180 − 152.5 = Sh 27.50
27.50 × 100% = 18.03%
152.5 - A = 15 × 6000 = 90000
P = 84000 − 20000 = 64000
90000= 64000(1+ r/100)15
1.40625 = (1 + r/100)15
1 + r/100 = 1.02299
r = 0.02299 × 100
r = 2.299% - h = 3 − 0 = 1
3
A = h(y1 + y2 + y3)x 0.5 1.5 2.5 y 1.125 2.125 4.125
=1(1.125+2.125+4.125) = 7.375 square units - y = kx²
√z
yn = k(1.05x)²
√0.81z
yn = 1.225xk
√z
= 22.5% increase - x + y = 10
yx − xy = 54
9y − 9x = 54
y − x = 6
y + x = 10
−2x = −4
x = 2
y = 8
xy = 28 - 80000 = 500000(1 − 15/100)n
0.36 = 0.85n
log 0.36 = n log 0.85
n = log 0.36 = 6.286yrs
0.85 - dy/dx = 6x2
y = 2x3 + C
5 = 2(1)3 + C
C = 3
y + 2x3 + 3 -
n = km
4m = 2
m = ½
½(4) = −5−x
2 = −5−x
7 = −x
x = −7 -
-
-
- P(ABB) or P(ARR) or P(BBB) or P(BRR)
(½ × 2/5 × ¼) + (½ × 3/5 × 2/4) + (½ × 3/5 × 2/4) + (½ × 3/5 × ¼)
1/20 + 3/20 + 3/20 + 1/20 = 2/5 - P(ARB) or P(BRB)
(½ × 3/5 × ½) + (½ × 2/5 × ¾)
3/20 + 3/20 = 3/10 - 1 − (P(ARR) or P(BRR))
1 − ((½ × 2/5 × ¼) + (½ × 3/5 × 2/4))
1 − 1/5 = 4/5 - P(ABR) or P(ARB) or P(BRB) or P(BBR)
(½ × 2/5 × ¾) + (½ × 3/5 × 2/4) + (½ × 2/5 × ¾) + (½ × 3/5 × 2/4)
6/40 + 6/40 + 6/40 + 6/40
= 24/40 = 3/5
- P(ABB) or P(ARR) or P(BBB) or P(BRR)
-
-
- a + d = 8
a + 4d = 17
−3d = −9
d = 3
a + 3 = 8
a = 5
d = 3 - 2nd = 5 + 3 = 8
10th = 5 + 27 = 32
42nd = 5 + 123 = 128
∴ G.P. is 8, 32, 128
a = 8
r = 32/8 = 4
T10 = arn−1
T10 = 8(4)9
=2097152 - Sn = a(rⁿ − 1)
r − 1
= 8(4¹⁰ − 1)
4−1
= 8/3 (1048575)
= 2,796,200
- a + d = 8
-
Height in cm 1-5 6-10 11-15 16-20 21-25 26-30 31-35 36-40 41-45 46-50 Number of plants 1 3 5 6 7 7 7 7 5 2 C.F 1 4 9 15 22 29 36 43 48 50 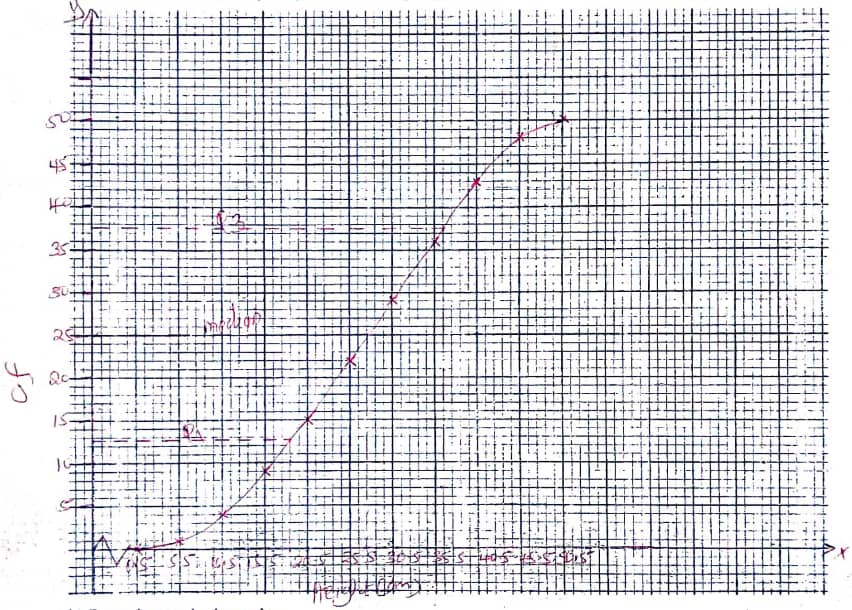
-
- 27.5cm
- Q1 = 18.5
Q3 = .36.5
36.5 − 18.5 = 18/2 = 9
2 - 18.5 to 36.5 or 18.35-36.5
= 18
-
X −3 −2 −1 0 1 2 3 4 3x2 27 12 3 0 3 12 27 48 −2x 6 4 2 0 −2 −4 −6 −8 −1 −1 −1 −1 −1 −1 −1 −1 −1 Y 32 15 4 −1 0 7 20 39 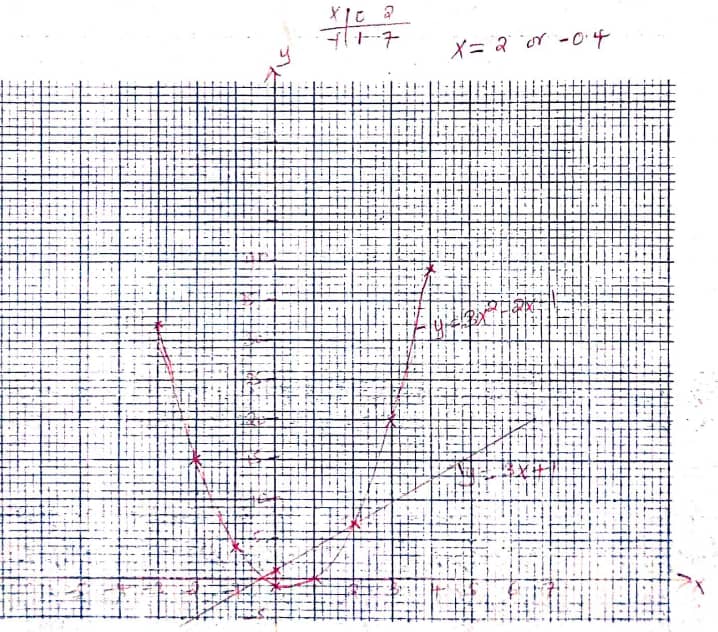
-
- BO = √(14²+14²) = 19.799cm = 9.899cm
2 2
VO = √(20² − 9.899²) = 17.38cm
VN = √(20² − 7²) = 18.73cm - Sin θ = 7 = 0.3737
18.73
θ = Sin−1 0.3737
= 21.94° - tan θ = 17.38
9.899
θ = tan−11.756
θ = 60.34° - 1/3 × 14 × 14 × 17.38 = 1125.49cm3
- BO = √(14²+14²) = 19.799cm = 9.899cm
-
-
A'(0,0) B'(4,2) C'(7,−4) D'(3,−6) -
A''(0,0) B''(−2, −4) C''(4,−7) D''(6,−3)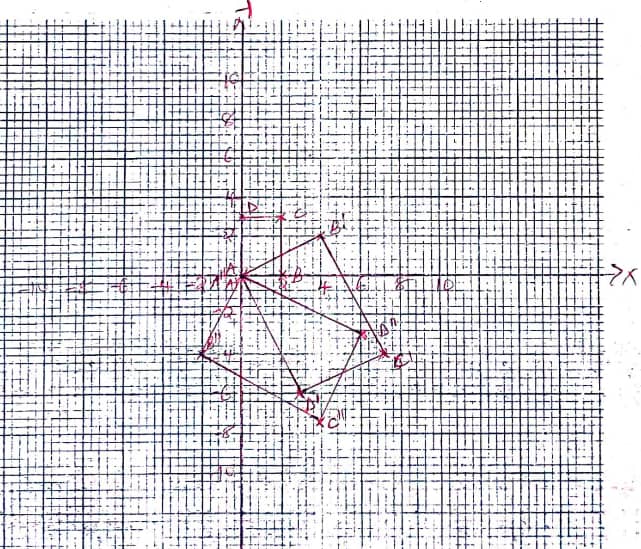
-
−2a−4b = 2
6a − 3b = 0
3b = 6a
b = 2a
−2a −4(2a) = 2
−2a − 8a = 2
−10a = 2
a = −0.2
b = 2(−0.2)
= −0.4
−2c − 4d = 0 ; 4d = −2c
4c − 7d = 3 c = −2d
4(−2d) −7d = 3
−15d = 3 ; d = −0.2
c = −0.4
-
-
-
-
V = 3/2t2 − 3t + C
5 = 3/2(2)2 −3(2) +C
5 = C
V = 3/2t2 − 3t + 5
V = 3/2 (4)2 − 3(40 + 5
24 − 12 + 5
=17m/s -
S = ½t3 − 3/2t2 + 5t + C
S = 0, t = 0, C = 0
S = ½t3 − 3/2t2 + 5t
S = ½(4)3 − 3/2(4)2 + 5(4)
32 − 24 + 20
= 28m
-
-

-
-
-
- θ = 50 − 15 = 35°
35 × 60 = 2100nm - θ = 60 + 20 = 80°
80 × 60 Cos 50° = 3085.38nm
3085.38 + 2100nm
= 5185.38nm
- θ = 50 − 15 = 35°
-
- θ = 60 + 20 = 80°
1° = 4 mins
80° = x
x = 80 × 4 = 320mins
1 60
= 5h 20 mins
0250
+520
0810
=0810hrs - t = 5185.38
900
= 5 hrs 46 mins
+3hrs 00mins
8hrs 46mins
0810
+ 846
1656
=1656hrs
- θ = 60 + 20 = 80°
-
Download Mathematics Paper 2 Questions and Answers - Lanjet Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students