INSTRUCTIONS TO THE CANDIDATES
- Write your name and Random no. the spaces provided above.
- Sign and write date of examination in the spaces provided above.
- This paper consists of two sections; SectionI and Section II.
- Answer All questions in Section I and only Five questions from section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations giving answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- This paper consists of 16 printed pages.
- Candidates should check the question paper to ascertain that all pages are printed as indicated and that no questions are missing.
- Candidates should answer questions in English.
SECTION I (50 MARKS)
Attempt all questions in this section
- Evaluate -4 of (-4 + -5 ÷ 15) + -3 -4 ÷ 2 (3 mks)
84 ÷ -7 + 3 - -5 - Simplify 9x2 - 1 (1 mk)
3x2 +2x + 1 - Evaluate without using a calculator or mathematical table leaving your answers as a simplified fraction. (2 mks)
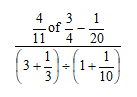
- A poultry farmer has twenty times as many hens as turkey and three quarters as many ducks as turkeys.
- If there are t, turkeys, write down a simplified expression in terms of t for the total number of birds on the farm. (1 mk)
- Give that he has 72 ducks, calculate as a percentage the sum of turkeys and ducks to the number of hens in the farm. (2 mks)
- Use tables of reciprocals only to work out. (3 mks)
5 + 12
0.0396 0.593 - A straight lines passes through points A(-2,6) and B(4, 2).
- M is the midpoint of line AB. find the coordinates of N. (2 mks)
- Determine the equation of a straight line passing through point M and is perpendicular to AB. (2 mks)
- An open right circular core has radius of 5cm and a perpendicular height of 12cm. Calculate the surface area of the core. (take π =3.142). (3 mks)
- Moraa spends a total of sh. 970 on buying 3 text books and 5 pens. if had bought 2 textbooks and 8 pens she would have saved sh. 90. Find the cost of one textbook. (3 mks)
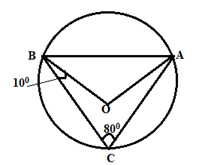
- In the figure below O is the centre of the circle. <BCA =80º and <CBO = 10º. Determine the size of <CAB. (3 mks)
- The table below shows speeds of vehicles measured to the nearest 10km/h as they passed a certain point.
Speed(km/h) 30 40 50 60 70 80 90 100 110 Frequency 1 4 9 14 38 47 51 32 4 - Calculate the mean speed of vehicles (3 marks)
- State the modal speed (1mark)
- Find the of x if. (3 mks)
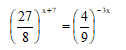
- The image of a point K(1,2) after translation is K1(-1,2). what is the coordinate of the point R whose image is R1 (-3,3) after undergoing the same translation. (3 mks)
- The figure below is a velocity time graph for a car.
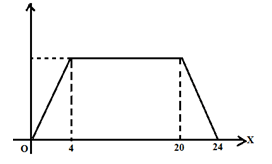
- Find the total distance travelled by the car (2 mks)
- Calculate the deceleration of the car. (2 mks)
- Security light poles have been erected along both sides of a street in Kisii town. The poles are 50m apart along the left hand side of the road while they are 80m apart along the right hand side. At one end of the road the poles are directly opposite each other. How many poles will be erected by time the poles are directly opposite each other at end of the road? (3 mks)
- The exterior angle of a regular polygon is equal to one third of the interior angle. Calculate the number of number of sides of the polygon. (3 mks)
- Solve the following inequality and state the integral values
½ (24-4x) > 6(3x-4/3)≥-2/3(42+3x) (3 mks)
SECTION II
Attempt only FIVE questions from this section -
- Complete the table below for the function y=7 + 2x - 2 x 2 for the range -3≤ x ≤ 4.(2 marks)
x -3 -2 -1 0 1 2 3 4 -2x2 -8 -2 0 -8 -18 2x -6 -4 0 4 6 7 7 7 7 7 7 7 7 7 y -5 7 3 -5 -
- On the grid provided draw the graph of y=7 + 2x - 2x2 . (3 marks)
Take the scale:2 cm to represent 1 unit on x- axis
1 cm to represent 1 unit on y- axis
- Use your graph to estimate the roots of 7 + 2x - 2 x 2 = 0. (1 mark)
- On the grid provided draw the graph of y=7 + 2x - 2x2 . (3 marks)
-
- By drawing a suitable line on the same axes in (b) above solve the equation
9 + 5x - 2 x 2 = 0 (3marks) - State the co-ordinates of the turning point .(1 mark)
- By drawing a suitable line on the same axes in (b) above solve the equation
- Complete the table below for the function y=7 + 2x - 2 x 2 for the range -3≤ x ≤ 4.(2 marks)
- Paul is a sales executive earning sh 20,000 and a commission of 8% for the sales in excess of 100,000. In January 2014 he earned a total of 48000 in salaries and commissions.
- Determine the amount of sales he made in that month. (4 mks)
- If the total sales inn the month of February and march increased by 18% and then dropped by 25% respectively. Calculate.
- Paul`s commission in the month of February. (3 mks)
- If the total earnings in the month of march. (3 mks)
- Two tasks are similar in shape. The capacity of the tanks are 1,000,000 litres and 512,00 litres respectively.
- Find the height of the smaller tank if the larger one is 300cm tall. (5 mks)
- Calculate the surface area of the tank if the smaller one has a surface area of 768cm3 (3 mks)
- Calculate the mass of the larger tank if the mass of the larger one is 800kg. (2 mks)
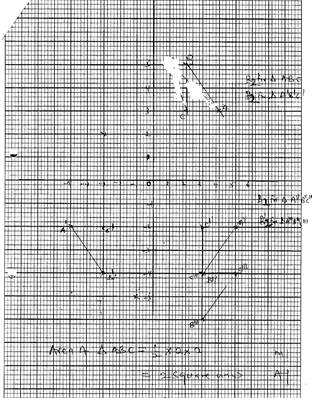
- The vertices of a triangle ABC are A(2,5) B(4,3) and C(2,3). P represents half-turn about the origin.
- Draw triangle ABC and A1B1C1 under P. (4 mks)
- T represents a reflection in the line x = 0 and K represents a translation . Find the coordinates of A11B11 and C11 under T and A111B111C111 under K. Hence, draw triangle A11B11C11. (4 mks)

- Find the area of the triangle A11B11C11. (2 mks)
- Ombati owns a farm that is triangular in shape as shown below.
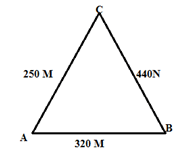
- Calculate the size angle BAC. (2 mks)
- Find the area of the farm in hectares. (3 mks)
- Ombati wishes to irrigate his farm using a sprinkler machine in the farm such that it is equidistant from points A. B and C.
- The sprinkler rotates in a circular motion so that the maximum point reached by the water jets is the vertices A, B and C. Calculate the area outside the farm that will be irrigated. (5 mks)
- Trasnsline bus left Nairobi at 8.00 am and travelled Kisii at an average speed of 80km/h. A car left Kisii at 3.30 am and travelled to Nairobi at an average speed of 120km/h. Given that the distance between Nairobi and Kisii is 400km, Calculate.
- The time the car arrived in arrived in Nairobi. (3 mks)
- The time the two vehicles met. (4 mks)
- The distance from Nairobi to the meeting point. (2 mks)
- The distance of the bus from Kisii when the car arrived in Nairobi. (2 mks)
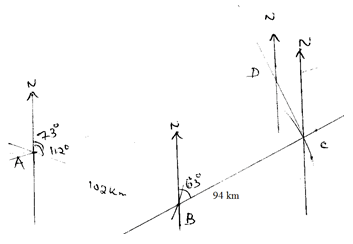
- Town B is 102km on the bearing of 122º from town A. Town C is 94 km on bearing of 062º from B. Town D is on a bearing of 073º from A and 336ºC.
- Using a scale of 1cm to represent 20km, draw a scale diagram to show the relative positions of town A, B, C and D. (4 mks)
- Using your diagram, determine.
- The bearing B from D. (1 mk)
- The bearing of A from C. (1 mk)
- The distance from town A to D. (1 mk)
- The distance from town B and D. (1 mk)
- A particle moves along a straight line such that its displacement S metres from a given point is
S=t3 - 5t2 + 3t +4 where t is time in seconds. Find- The displacement of the particle at t = 5 (2marks)
- The velocity of the particle when t = 5 (3 marks)
- The values of t when the particle is momentarily at rest (3 marks)
- Acceleration of the particle when t = 2 (2marks)

MARKING SCHEME
- -4 of (-4 - 3) + - 2 (3 mks)
-12 + 3 + 3
4 of (- 7 – 3 – 2)
- 4
48 = - 12
-4 - Nume (3x + 1) (3x - 1)
Den (3x – 1) ( x + 1)
(3x +1)(3x – 1)
(3x – 1) (x + 1)
3x + 1
x + 1 - 4 x 14
11 20
10 ÷ 11
3 10
= 4 x 7 x 33
7 10 100
= 21
250 - No . of hens = 20t, number of ducks = 3t/4
Total No = t + 20t + ¾ t
= 21 ¾ t
¾ t = 72
t = 96
Hens = 1920
96 + 72 x 100
1920
= 8.75% - 5 + 12
0.1396 0.593
65(7,161) + 12(1.686)
35.805 + 20.232
=56.037 - M = -2 + 4 , 6 + 2
2 2
=(1,4)
g1= - 2
3
g2 = 3
2
y - 4 = 3
x - 1 2
2y = 3x + 5 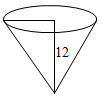
S.A = πrl
1 = √52 + 1212
=13cm
S.A = 3.142 x 5 - x 13
= 204.23- Let t and p be the cost of a text book and a pen respectively.
3t + 5p = 970 ………………(i)
2t + 8p = 880 ………………(ii)
Multiply (i) by 8 and (ii) by 5
24t + 40p = 7760
10t + 40p = 4400
104t = 3360
t = 240 - <BOA = 80 x 2 = 160º
Obtuse < BOA = 200º
Therefore < OAC + 80º + 200º + 10º = 360º
<OAC = 360º - 290º
= 70º
<CAB = 70 + (180 - 160)
2
= 800 -
Σfx = 200Speed(km/h) 30 40 50 60 70 80 90 100 110 Frequency 1 4 9 14 38 47 51 32 4 Fx 30 160 450 840 2660 3760 4590 3200 440
Σfx = 16,130
Σfx = 16130
Σf 200
= 80.65- 90km/h
B1
M1
A1
B1
(04)
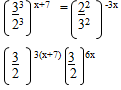
3(x + 7) = 6x
3x + 21 = 6x
3x = 21
x = 7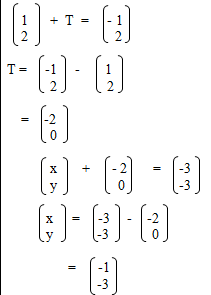
R(-1, -3)-
- = ½ + 4 x 80 + 80 x 16 + ½ x 4 x 80
= 160 + 1280 + 160
= 1600m - a = - 80
4
= 20m/s2
- = ½ + 4 x 80 + 80 x 16 + ½ x 4 x 80
- L.C.M of 50 and 80
=400
Number of poles = 400 + 400
50 8
= 13 - Ext + Interior = 1800
1/3x + x = 180
4/3x = 180
x = 180 x 3
4
Exterior =1/3 x 135 = 4500
No. of sides = 360
45
= 8 sides - 12 – 2x >18x – 8 > 28 – 2x
12 + 8> 18x +2x
x< 1
18x + 2x > - 28 + 8
x > -1
- 1 < x <1
Intergral values are 0 and -1 -
x -3 -4 1 4 -2x2 -18 -2 -2 -32 2x -6 -2 2 8 y -17 3 7 -17 -
- x = -15 or 2.5
- 7+2x – 2x = 9 + 5x - 2x2
y = - 3x - 2
x = - 1.2 or 3.7 - (0.5, 7.5)
- 48000-20000
=28000
8 × x = 28000
100
= sh. 350, 000
Sales = 350 000+100 000
= 450 000- Sales for feb
118 × 480000
100
=531 000 - 100 000
= 431 000 × 8
100
=34, 480 - 75 × 531 000
100
=sh. 398 250
Commission = 298250 × 8
100
= 23, 860
sh 23860 + 20 000
= 43 860
- Sales for feb
- V.S.F = 512000: 100000
512: 1000
64: 125
43: 53
L.S.F
Height os small tank = 4 x 300
5
= 240cm
A.S.F = 16: 25
S.A of the large tank = 25 x 768
16
= 1200m2
Mass of smaller tank = 125 x 800
64
= 1562 -
-
- Cos Ө = 2502 + 3202 - 440
2 x 250 x 320
= 100.33º - A = ½ x 250 x 320 sin 100.33º
= 39351.65
10000
= 3.9352ha - 2R = 440
Sin100.33
R = 223.6
A = 22 x 223.62 - 39351.65
7
=117781.7m2
- Cos Ө = 2502 + 3202 - 440
-
- Time the arrives in NBI = 400
120
= 3hrs 20 min
Time = 8.20am + 3.20min
= 11.50am - Distance covered by the bus in 30min
= ½ x 80 = 40km
Time taken to meet = Distance
R.S
= 360
200
= 1hr 48min - Distance = 40 + 9/5 x 80
= 40 + 144
= 184km - Distance = 80 x 23
6
= 360 2/3 km
- Time the arrives in NBI = 400
- Bearing of B from D = 212 ± 11
- Bearing of A from C = 269 ± 10
- Distance of A from C = 8.4cm ± 0.1cm
= 168km ± 2 - B from D = 4.8cm ± 0.1cm
= 96km ± 2
-
- S = 53 - 5(5)2 + 3(5) + 4
S = 19 - V = ds = 3t2 – 10t + 3
dt
= 3(5)2 - 10(5) + 3
= 28m/s - Moment at rest V = 0
3t2 – 10t + 3 = 0
(3t – 1) (t – 3) = 0
t = ⅓ or 3sec - Acceleration when t = 2
a = dv/dt = 6t – 10
= 2m/s2
- S = 53 - 5(5)2 + 3(5) + 4
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

