Open menu

Mathematics Paper 2 Questions and Answers - Samia Joint Mock Examination 2021/2022

Share via Whatsapp

« Previous Topic
Mathematics Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022

Next Topic »
English Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS TO THE CANDIDATES

  1. Write your name and index number in the spaces provided above.
  2. Sign and write the date of examination in the spaces provided above.
  3. This paper consists of TWO sections; Section I and II.
  4. Answer ALL the questions in sections 1 and ONLY FIVE questions from section II
  5. Show all your steps in your calculations, giving your answers at each stage in the spaces provided below each question.
  6. Marks may be given for correct working even if the answer is wrong.
  7. Non – programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
  8. Candidates should answer questions in English.

SECTION 1 (50 marks)
Answer ALL questions in this section in the spaces provided.

  1. The external and internal radius of a cylindrical cement pipe are given as 20cm and 14cm respectively and its length is given as 140cm. Calculate the minimum volume of cement required to make such pipe. (Take π = 3.142) (3mks)
  2. Solve for x in the equation 2sin2x + 3cosx = - 1 for 0º< x <360º (4mks)
  3. A quadratic curve cuts the x – axis at points (-2, 0) and (3, 0). Find the equation of this curve in the form ax2 + by = c where a, b and c are integers. (3mks)
  4. Expand (2 + 3x)6 up to the term in x3. Hence use your expansion to estimate (2.09)6 (3mks)
  5. Two quantities M and N are such that M varies partly as N and partly as the square of N. Determine the relationship between M and N given that when M is 1050, N = 10 and when M = 2200, N = 20. (3mks)
  6. A dealer has two types of grades of tea, A and B. Grade A costs shs. 140 per kg while grade B costs shs.160 per kg. If the dealer mixes A and B in the ratio 3:5 to make a brand of tea which he sells at shs.180 per kg, calculate his percentage profit. (3mks)
  7. The position vectors of A and B are given as a = 2i -3j + 4k and b = -2i - j + 2k respectively. Find to 2 decimal places, the length of the vector AB. (3mks)
  8. Calculate the quartile deviation in
    18, 9, 14, 20, 23, 12, 16 (3mks)
  9. Find the equation of a circle whose radius is 0.75 units and centre coordinates (0.75, -0.5). Leave your answer in the form;
    x2 + y2 + ax + by + c = 0 (3mks)
  10. Solve for the exact value of x in the equation. (3mks)
    2log10x + log105 = 1 + 2log104
  11. A plane leaves an airport A (38.50N, 37.050W) and flies due North to a point B on latitude 520N. The plane then flies due East to a point C 2400km from B. Determine the position of C. (Given that the radius of the earth is 6371km) (3mks)
  12. Evaluate ɭ3-1(2x2 – 3x – 14)dx (3mks)
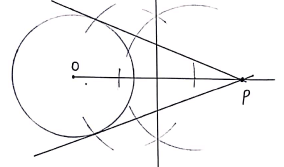
  13. Using a ruler and a pair of compass only, construct common tangents from the point P to the circle below. (3mks)
    1
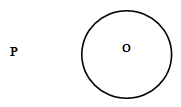
  14. Given that 3 + 3√5   3 -√5 = a + b√5. Find the values of a and b. (3mks)
                      3 + √5 
  15. In the figure below angle CBD = 370, angle BCD = 200 and ABC is a tangent to the circle at B.
    2
    Find:
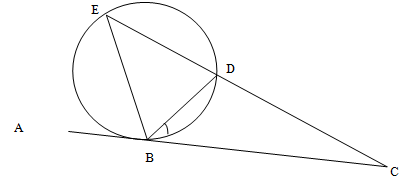
    1. Angle BED (2mks)
    2. Angle ABE (2mks)
  16. A transformation is represented by the matrix 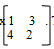3 . This transformation maps a triangle
    ABC of the area 12.5cm2 onto another triangle ABC of the area 12.5cm2 onto another triangle A1B1C1. Find the area of triangle A1B1C1. (3mks)

    SECTION II(50marks)
    Answer ANY FIVE questions in this section in the spaces provided
  17. A transformation represented by matrix 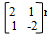4maps A(0,0), B(2,0), C(2,3) and D(0,3)
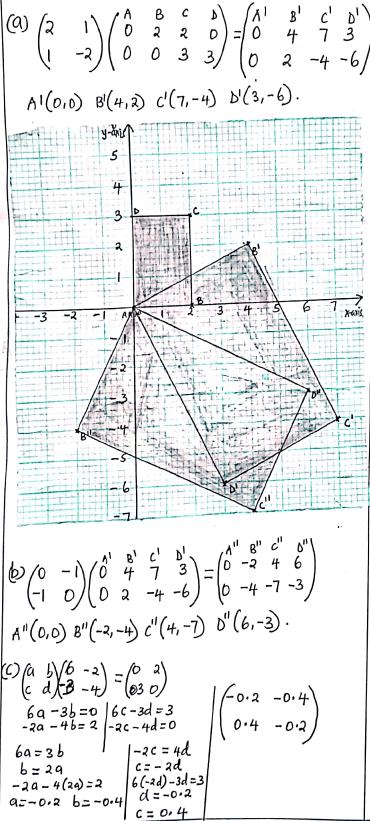
    Onto A1B1C1 and D1 respectively
    1. Draw ABCD and its image A1B1C1D1 (4mks)
    2. A transformation represented by 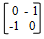5 maps A1B1C1D1 on A11B11C11D11.
      Plot A11B11C11D11on the same graph. (3mks)
    3. Determine the matrix of a single transformation that maps A11B11C11D11. onto ABCD. (3mks)
  18. The diagram below shows a right pyramid with a square base ABCD and vertex V. O is the centre of the base. AB = 14m, VA = 20m and N is the midpoint of BC.
    6
    Find;
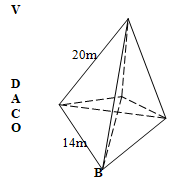
    1. The lengths of BO, VO and VN (3mks)
    2. The angle between VO and plane VBC (3mks)
    3. The angle between VB and base ABCD (2mks)
    4. The angle between VDC and VBC (2mks)
  19. The table below shows the distribution of marks scored in a test by standard 8 pupils in one school.
    Marks No. of pupils
    30 – 34 1 
    35 – 39 5
    40 – 44 10
    45 – 49 10
    50 – 54 19
    55 – 59 20
    60 – 64 20
    65 – 69 8
    70 – 74 4
    75 – 79 3
    Using 57 as the assumed mean mark, calculate
    1. The actual mean for the grouped marks (3mks)
    2. The 50th percentile (3mks)
    3. The standard deviation of the marks (4mks)
  20.      
    1. Complete the table for the function y = ½ Sin2x, where 00< x< 3600. (2mks)
      x  0º  30º  60º 90º 120º 150º 180º 210º 240º 270º 300º 330º 360º
      2x  0º  60º 120º 180º 240º 300º 360º 420º 480º 540º 600º 660º 720º
      Sin2x 0º  0.866     0º       0.866        
      y = ½ Sin2x 0º  0.433     0º                
    2. On the grid provided, draw the graph of the function y = ½ Sin2x for 00<x<3600 using the scale 1cm for 300 on the horizontal axis and 4cm for 1 unit of y axis. (3mks)
    3. Use your graph to determine the amplitude and period of the function y = ½ Sin2x.(2mks)
    4. Use the graph to solve
      1. ½ Sin2xº = 0 (1mk)
      2. ½ Sin 2xº – 0.5 = 0 (2mks)
  21. Income tax rate were charged as follows in a given year.
    Income in ksh. p.m Rate of tax in each sh.
    1 – 11, 180  10%
    11, 181, - 21, 714  15%
    21, 715 – 32, 248  20% 
    32, 249 – 42, 781   25% 
    42, 782 and above 30% 
    A teacher earns a basic salary of Ksh. 48, 000. He is housed by the employer and pays a rent of Ksh. 3,000 per month. His allowances are: Commuter Ksh. 2, 500 and medical Ksh. 3,500. He is entitled to a family relief of Ksh. 1,648 per month.
    Determine his:
    1. Taxable income per month (2mks)
    2. Net tax per month (4mks)
    3. In addition the following deductions are also made
      NHIF Ksh. 1,250
      WCPS Ksh. 1,200
      Co – operative shares Ksh. 3,000
      Calculate the net salary. (3mks)
  22.      
    1. The first term of an Arthmetric progression (AP) is 2. The sum of the first 8 terms of the AP is 156
      1. Find the common difference of the AP (2mks)
      2. Given that the sum of the first n terms of the AP is 416, find n (2mks)
    2. The 3rd, 5th and 8th terms of another AP form the first three terms of a Geometric Progression (GP). If the common difference of the AP is 3, find;
      1. The first term of the GP; (4mks)
      2. The sum of the first 9 terms of the GP, to 4 significant figures. (2mks)
  23. A married couple intends to have 3 children. They consult an expert who tells them that the probability of a male birth is 0.55.
    1. Draw a tree diagram to represent this occurrence (2mks)
    2. Find the probability that
      1. All the three children will be female (2mks)
      2. At least a male is born (2mks)
      3. At least 2 will be females, giving your answer to 3 s.f. (4mks)
  24. A trader is required to supply two types of sweaters, type A and type B. the total number of sweaters must not be more than 400. He has to supply more of type A than type B sweaters. However the number of type A sweaters must not be more than 300 and the number of type Bsweaters must not be less than 80. Let x be the number of type A sweaters and y be the number of type B sweaters.
    1. Write down in terms of x and y all the linear inequalities representing the information above. (4mks)
    2. On the grid provided, draw the inequalities and shade the unwanted regions.(4mks)
    3. The profits were as follows;
      Type A: sh. 600 per sweater
      Type B: sh. 400 per sweater
      1. Use the graph to determine the number of sweaters of each type that he should make to maximize the profit. (1mk)
      2. Calculate the maximum possible profit (1mk)

MARKING SCHEME

  1. πR2H(min) - πr2h(max) 
    (3.142 x 19.52 x 139.5) - (3.142 x 14.52 x 140.5)
    = 166,666.9973 - 92815.07275
    = 73851.92455
  2. 2(1 - cos2x) + 3cosx - 1 = 0
    2 - 2cos2x - 3cosx - 1 = 0
    2cos2x - 3cosx - 1 = 0
    let cosx = y
    2y2 - 3y - 1 = 0
    y =3 ± √9 + 8 = 3 ± √17
               4                 4
    = 1.780776406
    - 0.280776406
    cosx = 1.780776406
    cosx = - 0.280776406 = 73.69º
    ∴ x = 180 - 73.69 = 106.31
    x = 180 + 73.69 = 253.69
  3. (-2,0)(3,0)
    (x + 2)(x - 3) = 0
    x(x - 3) +2(x - 3) = 0; 
    x2 - 3x + 2x - 6 = 0
    x2 - x = 6
  4.    26     25     24     23
    (3x)2 (3x)1 (3x)2 (3x)3 
    1      6         15     20
    64 + 576x + 2160x2 + 4320x3 
    2 + 3x = 2.09x = 0.03
    64 + 576(0.03) + 2160(0.03)2 + 4320(0.03)3
    = 83.34064
  5. M = KN + CN2 
    1050 = 10K + 100C
    2200 = 20K + 400C
    2100 = 20K + 200C
    2200 = 20K + 400C
    +100 = -200C
    -200      -200
    C = ½
    1050 = 10K + 50
    K = 100
    M = 100N + ½N2
  6.    A          B
    sh140   160
      3           5
    cost  price per kg of the mixture
    (140 x 3) + (160 x 5) = 152.50
                  8
    profit = 180 - 152.50 = 27.5
    %p =   27.5   x 100% = 182/61%
            152.50
  7. AB = B - A
    7
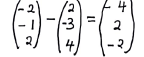
    √(-4)2 + 22 + (-2)2 = √24 = 4.90
  8. 9,12,14,16,18,20,23
    Q1 = 12   Q3 = 20
    20 - 12 = 8  = 4
        2         2
  9. R = 3/4 centre (3/4 - ½)
    (x - 3/4 )2 + (y + ½)2 =(3/4)2 
    x2 = 63x + 9  + y + y + ¼ = 9 
            42    16                      16
    x2 = 3x + y2 + y + 9   -  9  - ¼ 
            2                  16    16 
    x2 - 3x  + y2 + y = - ¼
           2
    4x2 + 4y2 - 6x + 4y + 1 = 0
  10. log10x2 + log5 = log1010 + log1016 
    log10(5x2) = log10(160)
    5x2 = 160
    √x2 = √32 = ±4√2
    x =  ±4√2
  11.   θ   x 2 x 22  x 6371cos52 = 2400
    360          7
    θ = 35.04º
    37.05 - 35.04 = 2.01
    C(52ºN, 2.01ºW)
  12.  2x3 - 3x2  - 14x + c 3-1
     3      2
    (2(3)3 - 3(3)2  - 14(3)) - (2(-1)3 - 3(-1)2  - 14(-1))
       3         2                        3          2
    (18 - 13.5 - 42) - (-2/3 - 3/2 + 14)
    - 37.5 - 115/6 
    = -49 ¹/3 
  13.    
    8
  14. (3(3 -√5) + 3√5(3 + √5) 
        (3 + √5)(3 - √5)
    9 - 3√5 + 9√5 + 15 
             9 - 5
    24 + 6√5 = 6 + 1.5√5
         4
    a = 6 and b = 1.5 or ½
  15.    
    1. ∠BED = 37º; angles in alternate segments
    2. ∠ABE = 57º; angles in alternate segment
  16. Det = (1 x 2) - (3 x 4) = -10
    Area of ΔA1B1C1 = 12.5 x -10 = -12.5
    = 125cm2
  17.    
    9
  18.    
    1. BO= √142 + 142  = 9.899
                     2
      VO = √202 - 9.8992 = 17.38
      VN = √72 + 17.382 = 18.74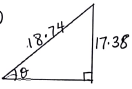

    2. 10
      Sinθ =17.38
                18.74
      = 68.04º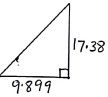

    3. 11
      Tanθ =17.38
                 9.899
      = 60.34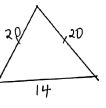

    4. 12
      Sinθ =9.899
                13.12
      = 48.99 x 2
      = 97.98º
  19.     
    Marks f x x - 57d fd d2 fd2 cf
    30 – 34 1  32 -25 -25 625 625 1
    35 – 39 5 37 -20 -100 400 2000 6
    40 – 44 10 42 -15 150 225 2250 16
    45 – 49 10 47 -10 -100 100 1000 26
    50 – 54 19 52 -5 -95 25 475 45
    55 – 59 20 57 0 0 0 0 65
    60 – 64 20 62 5 100 25 500 85
    65 – 69 8 67 10 80 100 800 93.
    70 – 74 4 72 15 60 225 900 97
    75 – 79 3 77 20 60 400 1200 100
      N=     Σfd = -170   Σfd2 = 9750  
    1. Actual mean
      X= A + Σfd 
                  Σf
      57 + (-170/100) = 55.30
    2. 50th percentile 
       50  x 100 = 50
      100
      54.5 +(50 - 45)5
                    20
      = 55.75
    3. Standard deviation 
      13
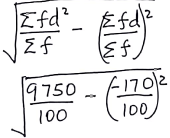
      = √94.61 = 9.726767192
  20.        
    1.    
      x  0º  30º  60º 90º 120º 150º 180º 210º 240º 270º 300º 330º 360º
      2x  0º  60º 120º 180º 240º 300º 360º 420º 480º 540º 600º 660º 720º
      Sin2x 0º  0.866 0.866  0º  -0.866 -0.866 0  0.866  0.866 0  -0.866  -0.866 0 
      y = ½ Sin2x 0º  0.433 0.433 0º  -0.433 -0.433 0  0.433 0.433 0  -0.433 -0.433 0 
    2.  
      14    
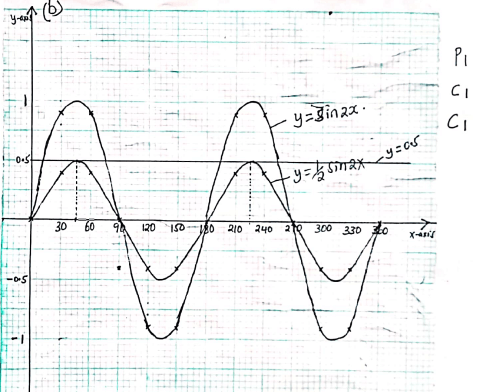
    3. Amplitude = 0.5
      Period = 180º
    4.      
      1. x = 0º,90º,180º,270º,360º
      2. x = 45º,225º
  21.      
    1. Taxable income per month
      115 x 48000 - 3000 + 2500 + 3500
      100
      = 58200
    2. 11180 x  10  = 1118
                   100
      10534 x 15  = 1580.10
                   100
      10534 x 20  = 2106.80
                   100
      10533 x 25  = 2633.25
                  100
      15419 x 30  = 4625.70
                   100
      1118 + 1580.10 + 2106.80 + 2633.25 + 4625.70
      = 12063.85
      12063.85 - 1648 = 10415.85
    3. Total deductions
      10415.85 + 1250 + 1200 + 3000
      15865.85
      58200 - 15865.85
      = 42334.15
  22.      
    1.    
      1. a = 2
        S8 =n/2(2a +(n - 1)d)
        156 = 8/2(4 + 7d)
        7d = 35   d =5
      2. 416 = n/2(4 +(n - 1)5)
        832 = 4n + 5n2 - 5n
        5n2 - n - 832 = 0
        n = 1 ± √1 + 16640129 = 1 ±129   n = 3
                       10                      10
        n = 13 only
    2.      
      1. a + 2d, a + 4d, a + 7d
        a + 4d = a + 7d
        a + 2d    a + 4d
        a2 + 8ad + 1bd2 = a2 + 9ad + 14d2
        ad = 2d2
        a = 2d ; a = 2 x 3 = 6
        a + 2d
        6 + 2(3) = 6 + 6 = 12
      2. a + 4d =6 + 4(3) = 1.5
        a + 2d       12
        S9 =a (rn - 1)
                   r - 1
        12(1.59 - 1) = 898.640625
           1.5 - 1
        = 898.6
  23.      
    1.       
      15
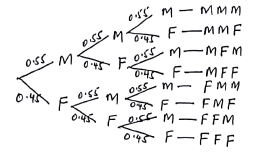
    2. P(FFF) = 0.45 x 0.45 x 0.45
      = 0.161125 or 729   = 0.908875
                            8000
    3. P(At least 2 females)
      P(MFF) or P(FMf) or P(FFM) + P(FFF)
      (0.55 x 0.45 x 0.45) + (0.45 x 0.55 x 0.45) + (0.45 x 0.45 x 0.55) + (0.45 x 0.45 x 0.45)
      = 0.425
  24.        
    1. x + y ≤ 400
      x >y 
      x ≤ 300
      y ≥ 80
    2.   
      16
    3. 600x + 400y = P
      1.   x   +   y   = 1
        100    180
        x = 300  y = 100
        Type A = 300
        Type B = 100
      2. 600(300) + 400(100)
        = 220,00
Join our whatsapp group for latest updates

Download Mathematics Paper 2 Questions and Answers - Samia Joint Mock Examination 2021/2022.


Tap Here to Download for 50/-


Why download?

  • ✔ To read offline at any time.
  • ✔ To Print at your convenience
  • ✔ Share Easily with Friends / Students

Read 10891 times Last modified on Friday, 28 January 2022 11:33

« Previous Topic
Mathematics Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022

Next Topic »
English Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022

Print PDF for future reference
Published in Samia Joint Mock Examination 2021/2022 Questions and Answers

Related items

back to top
Get on WhatsApp Download as PDF
.
Subscribe now

access all the content at an affordable rate
or
Buy any individual paper or notes as a pdf via MPESA
and get it sent to you via WhatsApp

 

What does our community say about us?

Join our community on:

  • easyelimu app
  • Telegram
  • facebook page
  • twitter page
  • Pinterest