Physics Paper 1 Questions and Answers - Samia Joint Mock Examination 2021/2022

INSTRUCTIONS

Write your name and index number in the spaces provided above
The paper consists of two sections, sections A and B
Answer all questions in section A and B in the spaces provided below each question
All answers and working must be clearly shown, marks may be awarded for correct steps even if the answers are wrong
Mathematical tables and silent electronic calculators may be used
Take g=10m/s²

SECTION A (25 MARKS)
Answer ALL the questions in this section in the spaces provided.

The figure below shows part of a vernier calipers when the jaws are closed without an object between the jaws.
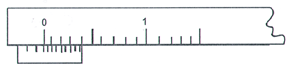
1. State the error of the vernier calipers. (1 mark)
2. A student used the vernier calipers to measure the diameter of a test tube whose actual diameter was 2.13cm. What was the reading shown by the vernier calipers? (2 marks)
A certain solid of volume 60cm³ displaces 20cm³ of a liquid when floating. If the density of the liquid is 600kgm^-3 determine the density of the solid (3 marks)
Name two forces that determine the shape of a liquid drop on a solid surface. (2 marks)
A uniform rod of length 4m and mass of 4kg is pivoted at 3.6m mark. The rod is held horizontal with a vertical rope at the 4m mark, as shown in figure 1 below.

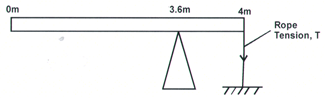
Calculate the tension, T in the rope. (Take g = 10N/kg) (3 marks)
The diagram below shows two similar cups of tea containing equal volumes of hot tea at the same level. It was observed that the rate of cooling was the same in the two cups. Explain. (2 marks)
A turntable of radius 10cm is rotating at 43 revolutions per second. Determine the linear speed of a point on the circumference of the turntable. (3 marks)
A trolley of mass 0.5kg moving with a velocity of 1.2ms^-1 collides inelastically with a second trolley of mass 1.5kg moving in the same direction with a velocity of 0.2ms^-1
1. What is an inelastic collision? (1 mark)
2. Determine the velocity of the trolleys after collision. (2 marks)
Figure 2 shows water flowing through two sections A and B of a pipe having x-sectional areas of 8cm² and 2cm² respectively.
1. Mark the appropriate level of water in the thermometer B. (1 mark)
2. The velocity of water as it flows past the wider section of the pipe is 0.6ms^-1. Calculate the velocity at the narrower section. (2 marks)
An electric motor raises a 60kg mass at a constant velocity. Calculate the power of the motor if it takes 30 seconds to raise the mass through a height of 25m. (take g = 10N/Kg) (3 marks)

SECTION B 55 MARKS

A mechanic uses a pulley system with a velocity ratio of 6 to raise engine of weight 2800N through a vertical distance of 1.5. The mechanic pulls with an effort of 500N. Calculate:
1. The effort distance 2mks
2. The work done by effort 2mks
3. The useful work done by the pulley machine 2mks
4. The mechanical advantage of the machine 2mks
5. The efficiency of the machine 2mks
6. State two reasons why the efficiency of a machine is always less than 100% 2mks
A ball of mass 50kg is thrown horizontally from the top of a cliff 20m high with a horizontal velocity of 20m as shown below on reaching the ground it completely covered piston x of a hydraulic lift such that no water splashes out. The other piston y has a weight of 25000N. assuming the top was opened when the ball struck the surface of water.

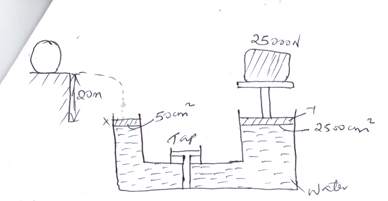
Determine:
1. The time taken by the ball to strike the surface of water at piston x 3mks
2. The distance from the foot of the cliff to where the ball strikes the surface of water. 2mks
3. The vertical velocity with which it struck the surface of water at piston x 2mks
4. The force with which the ball struck the surface of water 2mks
5. The distance moved by the 25000N load piston y if the level of water in piston x and piston y was initially the same. 3mks
1. Define latent heat of fusion 1mk
2. Water of mass 200g at a temperature of 60ºC is put in a well legged copper calorimeter of mass 80g. A piece of ice at OºC and mass 20g is placed in the calorimeter and the mixture stirred gently until all the ice melts. The final temperature of the mixture is then measured (latent heat of fusion of ice = 33400Jkg, S.H.C of water = 42000Jkg^-1k-.
  Determine:
  1. The heat absorbed by the mercury ice at OºC 2mks
  2. The heat absorbed by the melted ice to rise to temperature T 2mks
  3. The heat lost by the warm water and the calorimeter (S.H.C of the calorimeter = 900 Jkg^-1k. 2mks
  4. The final temperature T. of the mixture 3mks
Omukaga a form three physics student in a certain secondary school conducted an experiment purposed to establish relationship between normal reaction and frictional force between two surfaces. He measured the masses of the blocks of wood, then he hooked the blocks of wood on the spring balance and pulled each of them gradually in turn until the block just began to slide. He recorded the maximum reading registered by the spring balance for each of the block.

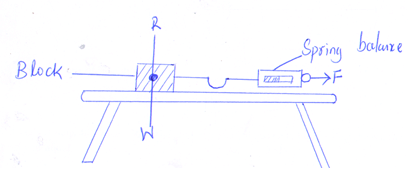
Mass of block(g) Normal reaction, R Spring balance reading

160 0.9

250 1.8

390 2.7

490 3.7

600 4.6

640 5.0
1. If g= 9.807 N/kg complete the table 2mks
2. Plot a graph of normal reactions R against spring balance reading 4mks
3. From the graph determine the gradient of the graph 3mks
4. What physical quantity does the gradient of the graph represent 1mk
5. What is the type of friction measured by the spring balance? 1mk
1. State the law of floatation 1mk
2. A body weighs 40N in air, 30N when in water and 35N when in liquid. Find the relative density of liquid. 3mks
3. A simple hydrometer is set up with a test-tube of mass 10g and length 12cm with a flat base and partly fixed with load shorts. The test-tube has a uniform cross-sectional area 2.0cm² and 10cm of its length is under water as shown in the figure below.
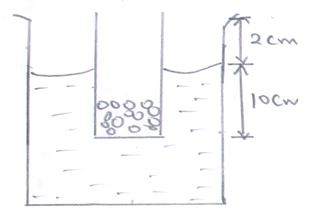
1. Taking the density of water as 1000kg/m³. Calculate the mass of the lead shorts in the tube 3mks
2. The mass of the lead shorts to be added if it has to displace an equal volume of a liquid of density 1.25g/cm³ 2mks

MARKING SCHEME

1. -0.02cm
2. 2.13 +0.02 = 2.15
mass displaced = (20 x 0.6)
=12g
Density = mass
volume
= ¹²/₆₀
= 0.2g/cm³
- Surface tension
- Weight of the drop
Clockwise moments = anti-clockwise moment
W x 1.6= T x 0.4
40 x 1.6 = 0.45T
T=40 x 16
0.4
= 160NV
A loses heat through evaporation because of the large surface area. B because dull surface is a good emitter of heat. (2 marks)
1 rev = 27°
43 rev = 43 x 2πº
= 86πº
ω= 270.212 c/sm
V = rw
= ¹⁰/₁₀₀ x 270.212 m/s = 27.0212 m/s
1. A collision in which objects combine / fuse, losing kinetic energy in the process
2. Final momentum = initial momentum
  (0.5 +1.5)V = (0.5 x 1.2)+(1.5 x 0.2)
  2.0V = 0,6 +0.3
  2.0V = 0.9
  V -0.45m/s
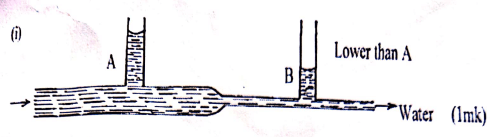
2. V_BA_B = V_AA_A
  V_B x 2 x 10^-4 = 0.6 x 8 x 10^-4
  V_B= 0.6 x 8 x 10^-4
  2 x 10^-4
  = 2.4ms^-1
Power = work done
time taken
force x distance moved
Time taken
= mg x d
t
= (60 x 10 x 25)W
30
= 500W

SECTION B

1. Effort distance = V.R x Ld
  = 6 x 1.5
  = 9m
2. Work done by effort = Effort x Effort distance
  = 500N x 9m
  = 4500J
3. Useful workdone = Load x Load distance
  2800 x 1.5
  = 4200J
4. M.A = L =2800 = 5.6
  E 500
5. Eff =M.A x 100
  V.R
  =5.6 x 100
  6
  = 93.33%
6. Friction between the moving parts of the machine
1. H = ½gt²
  20 = ½ x 10 x t²
  t = 2.0
2. R = ut
  = 20 x 2
  40m
3. V = u + at
  0 + 10(2)
  = 20m/s
4. F₁= F₂
  A₁ A₂
  F₁ =25000 x 50
  2500
  = 500N
5. Pressure due to water = hsg
  = h x 1500 x 10
  Pressure exerted = ^F/_A =25000 = 100,000N/m²
  0.25
  hsg = 100000
  10000h = 100000
  h = 10M
1. Quality of leaf required & change a mass of a substance from solid state to liquid state without change in temperature
2. 1. Heat absorbed by ice = M/F
    = 0.02 x 33400
    = 668J
  2. θ = mcθ
    = 0.02 x 4200T
    = 84TJoules
  3. Heat lost = mcθ + mcθ
    = 0.2 x 4200(60 - T) + 0.08 x 900 (60 - T)
    = 50400 - 840T + 4320 - 72T
    = 54720 - 912T
  4. Heat lost = Heat gaines
    54720 - 912T = 84T
    996T = 54720
    T = 54.94º
    ≈ 55ºC
1. Mass of block(g) Normal reaction, R Spring balance reading
  
  160 1.569 0.9
  
  250 2.425 1.8
  
  390 3.825 2.7
  
  490 4.805 3.7
  
  600 5.884 4.6
  
  640 6.276 5.0
2. Gradient = ΔR = 5.2 - 1.8
  ΔF 4.0 - 1.0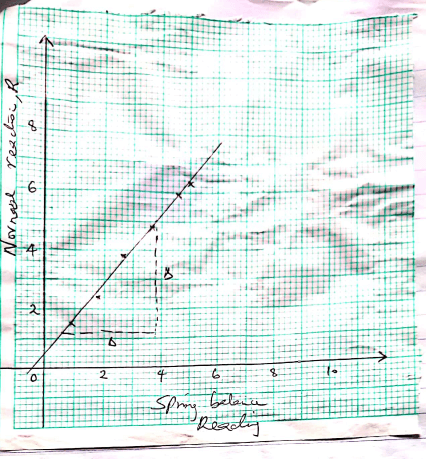
3. Gradient = ΔNormalReading =5.0 - 1.2
  ΔBalanceread 3.8 - 0.6
  = 1.188
4. Coefficient of friction
5. Static friction
1. A floating body displaces its own weight of the fluid in which it floats
2. Upthrust in water = 40 - 30 = 10N
  Upthrust in liquid x = 40 - 35 = 5N
  R.D = Upthrust in liq x = 5 = 0.5
  Upthrust in water 10
3. 1. Volume of water displaced = 2.0 x 10 = 20cm³Mass of water displaced = 20 x 1g/cm³
    Mass of lead shots = 20g - 10g = 10g or 0.01kg
  2. Mass of test tube and content = 20 x 1.25 = 25g
    Mass to be added = 35g - 20g = 5g