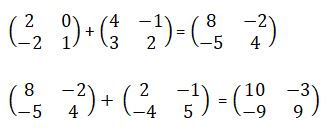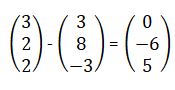MATHEMATICS
PAPER 1
Instructions
- The paper contains two sections A and B.
- Answer all questions in section A and any five questions from section B in the spaces provided below each question.
- Show all the steps in your calculations giving your answers at each stage in the spaces below each question.
- Non-programmable silent electronic calculator and mathematical tables may be used except where stated otherwise.

Questions
SECTION A
Answer all questions in this section in the spaces provided
- The sum of two numbers exceeds their product by one. Their difference is equal to their product less five. Find the two numbers. (3 marks)
- Musa has twenty shillings more than Aisha. After he spends a quarter of his money and Aisha ⅕ of hers, they find that Aisha has 10 shillings more than Musa. How much money did both have? (4 marks)
- The number 2942m08 is divisible by 11. Find the least value of m and the square of m. (3 marks)
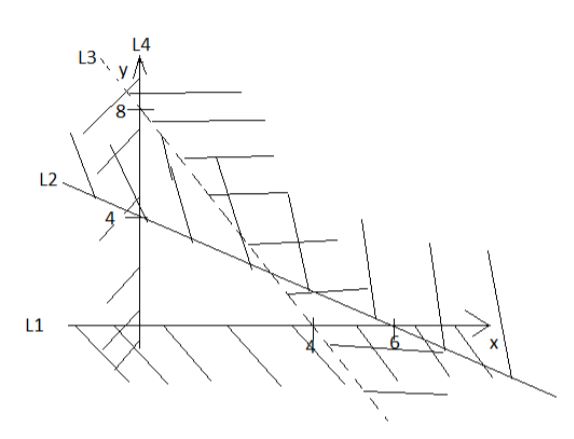
- Give the inequalities which define the region R in the diagram shown below. (3 marks)
- Given P =
, Q =
and R =
, find PQ + R. (3 marks)
- A Kenyan businessman bought goods from Japan worth 2,900,000 Japanese Yen. On arrival in Kenya, custom duty 10% was charged on the value of the goods. If the exchange rates were as follows:
1 US dollar = 118 Japanese Yen
1 US dollar = 78 Kenyan Shillings.
Calculate the duty paid in Kenya Shillings. (3 marks) - Solve the equation; (3 marks)
4x+22x+1=36 - Line AB is perpendicular to a line whose equation is y - 2x + 7= 0 and passes through point (-4, 5). Determine the equation of AB in the form y = mx + c. (3 marks)
- Simplify the following expression. (3 marks)
θ - 1
sin θ - Without using a calculator evaluate using squares, square roots and reciprocal tables the following:- (3 marks)
2 + 10
30.162 √588.3 - Two of the exterior angles of an irregular polygon are 63º each. The remaining exterior angles are each 26º. Determine the number of sides of the polygon. (3 marks)
- A number when divided by 10, 15 and 18, the reminders are 7, 12 and 15 respectively. Find the lowest number. (3 marks)
- The figure below shows part of a circle. Complete the circle and determine the radius and the centre of the circle. (3 marks)
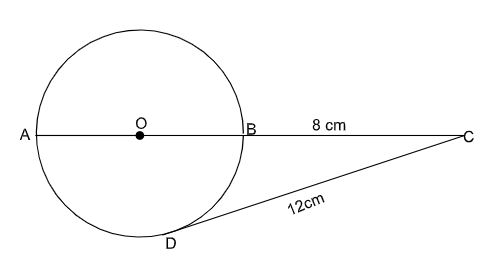
- In the figure below, DC is a tangent to the circle centre O at D. AOBC is a straight line meeting DC at C. DC = 12 and BC = 8. Find the radius of the circle. (3 marks)
- x varies directly as the cube of y and inversely as the square root of z. When x=24, y=2 and z=16. Find z in terms of x and y. (3 marks)
- Evaluate; -12∫ (-x3 + 5x - 2)dx (4 marks)
SECTION B
Answer any five questions in this section
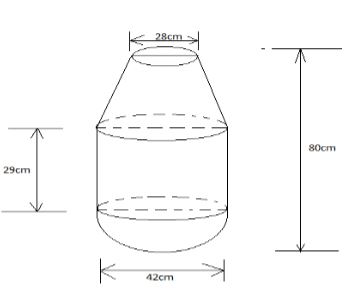
- The figure below is a model representing an open storage container. The model whose total height is 80 cm is made up of a frustum top, a hemispherical bottom and the middle part is cylindrical. The diameter of the top of the frustum is 28 cm, the base of the frustum diameter of the cylindrical and hemispherical part is 42 cm. The height of the cylindrical part is 29 cm.
- Calculate the surface area of the solid above (5 marks)
- The actual height of the container is 8 metres. Calculate the capacity of the container to the nearest litre. (5 marks)
- The table below shows marks scored by 40 students in a Mathematics test.
Marks 30-39 40-49 50-59 60-69 70-79 No. of students 2 10 13 8 7 - Using and assumed mean of 54.5, calculate the mean mark. ( 5 marks)
- Calculate the variance. (3 marks)
- Calculate the standard deviation. ( 2 marks)
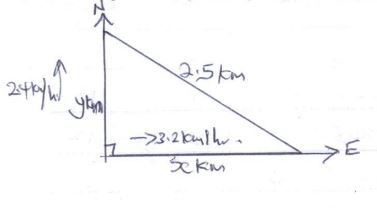
- Two policemen were together at a road junction. Each had a walkie talkie. The maximum distance at which one could communicate with the other was 2.5km. One of the policemen walked due East at 3.2km/h while the other walked due North at 2.4km/h. The policeman who headed east travelled for x km while the one who headed North travelled for y km before they were unable to communicate.
- Draw a sketch to represent the relative positions of the policemen. (1 mark)
-
- From the information above form two simultaneous equations in form of x and y. (2 marks)
- Find the value of x and y. (5 marks)
- Calculate the time taken before the police were unable to communicate. (2 marks)
-
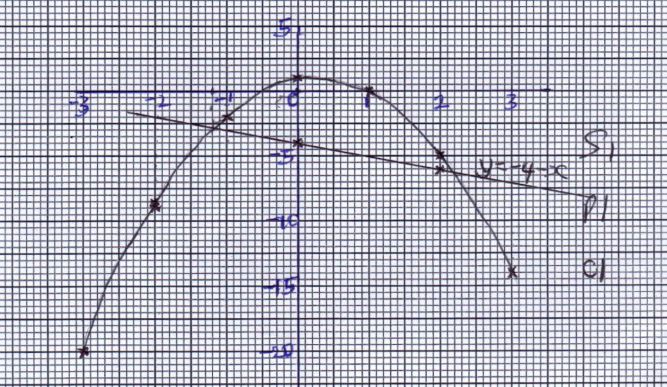
- Complete the table of the functions y = 1+x-2x2 (2marks)
x -3 -2 -1 0 1 2 3 -2x2 -18 0 -2 1 1 1 1 1 1 1 1 y -20 -9 0 - Draw the graph of the function y = 1+x -2x2 on the graph paper provided (3marks)
- Use your graph to find the value for x in the equations 1 + x -2x2=0 ( 1 mark)
- By drawing a suitable line graph on the same graph find the value for x which satisfies the equation 5 + 2x -2x2=0 (3marks)
- State the maximum point of the function y = 1+x -2x2 (1mark)
- Complete the table of the functions y = 1+x-2x2 (2marks)
-
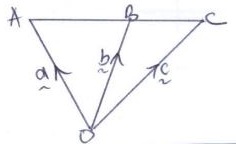
- The position vectors of points A and B are a and b respectively. C is another point with position vectors c= 64b - 24a . Express in terms of a and b vectors.
- →
AB (1 mark) - →
CB (1 mark) - →
CA (1 mark) - Show that A, B and C are collinear. (3 marks)
- Determine the ratio AB:BC (1 mark)
- → →
Given that OP=3i+8j-3k and OP=3i+2j+2k. Find |PQ| correct to 2dp. (3 marks)
- →
- The position vectors of points A and B are a and b respectively. C is another point with position vectors c= 64b - 24a . Express in terms of a and b vectors.
-
- Given a curve y=10 + 3x - x2 , use the trapezoidal rule with 5 trapezia to estimate the area bounded by the curve from x=-1 to x=4. (4 marks)
- Find the actual area under the curve by integration method from x=-1 to x=4. (4 marks)
- Find the percentage error introduced by the approximation. (2 marks)
-
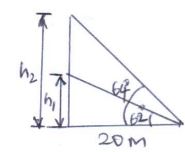
- A man standing 20m away from a building notices that the angles of elevation of the top and bottom of a flagpole mounted at the top of the building are 64º and 62º respectively. Calculate the height of the flagpole. (4 marks)
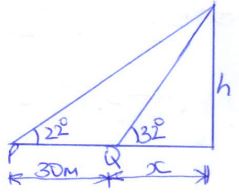
- The angles of elevation of the top of a tree from P and Q which are 30m apart are 22º and 32º respectively. Given that the two points are on the same side of the tree and on a straight line, determine the height of the tree. (6 marks)
- The displacement s metres after t seconds is given as s= -t3 + 3t2 + 4.
- Find its initial acceleration. (3 marks)
- Calculate;
- The time when the particle was momentarily at rest. (3 marks)
- The acceleration in m/s2 when t=3s (2 marks)
- Find the maximum velocity attained by the particle. (2 marks)

Marking Scheme
- ftx + y = xy -1
x - y = xy - 5
2y = 4
y=2
x=3 - 4/5x - 10 = 3/4( x+ 20)
4/5x - 3/4x = 15 + 10
x/20=25
x=500
Aisha has Ksh500
Musa - Ksh520
Both - Ksh1020 - 9 + 2 + 0 = 11
2 + 4 + m + 8 = 14 + m
14 + m= 22
m= 22 -14
m=8
m2 = 64 - L1 ⇒ y > 0
L4 ⇒ x > 0
L2 ⇒ (x/t) + (y/4) = 1 x 12
2x + 3y < 12
L3 ⇒ 8(x/4) + (y/8) = 1 x 8
2x + y < 8 -
- 10/100 x 2,900,000 = 2,900,000
2,900,000 x 78
118
= Ksh 191, 694.92 - (22)x + 22x x 21 = 36
22x + 2x x 21 = 36
22x( 1+2)=36/3
22x = 12
log 22x = LOg 12
2xLOg 2 = LOg 12
2x= Log12/Log2
2x=3.585
x= 1.7925 - y = 2x -7
Gradient of AB = -1/2
y-5 = -1/2
x+4
2(y-5) = -1(x+4)
2y-10 = -x-4
2y=-x+6
y= -1/2x + 3 - Sin2θ/Sinθ
Sin θ - 2 + 10
(3.016 x 10)2 √5.883 x 102
2 + 10
9.097 x 102 2.425 x 10
(2 x 0.001099) + (10 x 0.0412)
0.002198 + 0.412
0.414198 - Let the sides = n
(63 x 2) + 26(n-2) = 360
126 + 26n - 52= 360
26n + 74 = 360
26n = 286
n=11 -
2 10 15 18 3 5 15 9 3 5 5 3 3 5 5 1 5 1 1 1
2 x 33 x 5= 270
270 - 3 = 267 -
- 122 = (AB + 8)8
144 = 8AB + 64
144 - 64= 8AB
AB= 80/8
AB=10
Radius=5cm - xαy3
√z
x= ky3
√z
24 = K(2)3
√16
24= 8k/4
k=12
(x)2 = (12y3/√z)2
z= 144y6 - [-x⁴/4 + 5x²/2 - 2x]²
[-(2)⁴/4 + 5(2)²/2 - (2)2] - [ -(-1)⁴/4 + 5(-1)²/2 -2(-1)]
[-16/4 + 20/2 - 4] - [-1/4 + 5/2 + 2]
[2] - [17/4]
-9/4 = -21/4 -
- Lsf = 21:14
3:2
30 + x = 3/2
x
2(30+x) = 3x
60 + 2x = 3x
60=x
SA of cone
L√ g2 + 212
22/7 x 21 x 92.42
= 6099.72
SA of smaller cone = 6099.72 x 4 = 2710.99
9
SA of frustrum = 6099.72 - 2710.99 = 3388.73
SA of cylinder = 22/7 x 2 x 21 x 29 = 3828
SA of hemisphere = 2 x 22/7 x 212 = 2772
Total SA of model = 9983.73 - Volume of cone = 1/3 x 22/7 x 212 x 90 = 41580cm3
1/3 x 22/7 x 142 x 60 = 12320
Volume of frustrum = (41580 - 12320) = 29260
Volume of cylinder 22/7 x 212 x 29 = 40194
Volume of hemisphere = 1/2 x 4/3 x 22/7 x 213 =19404
Total = 88858 cm3
88.858 x 1000
88858 Litres
- Lsf = 21:14
-
-
Marks f x d=x-A t=d/10 ft ft2 30-39 2 34.5 -20 -2 -4 8 40-49 10 44.5 -10 -1 -10 10 50-59 13 54.5 0 0 13 0 60-69 8 64.5 10 1 8 8 70-79 7 74.5 20 2 14 28 Σf=40 Σft=21 Σft2 = 62
mean = (21/40 x 10) =+ 54.5
=5.25 + 54.5
= 59.75 - variance= s2 = [62/40 - (21/40)2] x 10 x10]
= 127.4375 - Standard deviation= s = √127.4375
=11.2888
=11.29
-
-
-
-
- y2 + x2 = 2.52 ⇒ y2 + x2 = 6.25
y/3.4 = x/3.2 ⇒ 3.2y=2.4 x , y= 2.4/3.2x - y2 + x2 = 6.25
(2.4x/3.2)2 + x2=5.25
5.76x2 + x2 = 6.25
10.24
1.5625x2 = 6.25
x2= 6.25/1.5625 = 4
x=√4=2
y2 + 22 = 6.25
y2= 6.25 -4
y=√2.25
y=1.5 - 2/3.2 = 0.625
=37.5
- y2 + x2 = 2.52 ⇒ y2 + x2 = 6.25
-
-
-
x -3 -2 -1 0 1 2 3 -2x2 -18 -8 -2 0 -2 -8 -18 1 1 1 1 1 1 1 1 y -20 -9 -2 1 0 -5 -14 -
-
- 1 + x - 2x2 =y
x = -0.5 and x=1
x= -1.2 ± 0.1 - x= 2.2 ± 0.1
Max (0,1)
- 1 + x - 2x2 =y
-
-
-
-
→
AB = b - a - →
CB
= -6/4b + 2/4 a + b
1/2a - 1/2b - →
CA
-6/4 b + 2/4a + a
3/2a - 3/2b - AB = kBe
b-a = k(1/2b - 1/2c)
k=2
AB=2BC
AB//BC
B is in common hence collinear - AB:BC = 2:1
-
-
PQ=
|PQ| = √(02 + (-6)2 + (5)2
=√61 = 7.81
-
-
-
y=10 + 3x - x2x -1 0 1 2 3 4 y 6 10 12 12 10 6
A= 1/2 x 1[(6 + 6) + 2(10 + 12 + 12 +10)
=1/2[(12) +88]
50sq units - 4-1∫(10 + 3x - x2)dx = [10x + 3x²/2 - x3/3]4-1
[10(4) + 3(4)²/2 - (4)³] - [10(-1) +3(-1)²/2+(-1)³/3]
(422/3) - (-81/6)
305/6 = 505/6
( dont accept decimal) - AE = 505/6 - 50 = 5/6
% ⁵/₆ x 100 = 100/6 = 139/61%
505/6
-
-
tan 62º = h1/20 ⇒ h1 = 37.61m
tan 64º = h2/20 ⇒ h2 = 41.01m
h2 -h1 = 41.01 - 37.61
= 3.4m-
- xtan 32º=h
- (x+30)tan22º=h
x tan 32=(x+30)tan22º
0.6249x= 0.404x + 12.12
0.2209x=12.12
x= 54.87
h=54.87tan32
=34.29m
-
- v=ds/dt = 3t2 + 6t ⇒ v=-3t2 + 6t
a=dv/dt = -6t + 6 → a = -6t + 6
initial acc. when t=0
a=-6(0) + 6
a = 6ms-2 -
- at rest v=0
-3t2+6t=0
3t(-t+2)=0
t=0
t=2 sec - a= -6(3) + 6
= -18+6
= -12m/s2
- at rest v=0
- -16t + 6=0
6=6t
t=1 sec
v= -3(1)2+6(1)
v=3ms-1
- v=ds/dt = 3t2 + 6t ⇒ v=-3t2 + 6t
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Mokasa II Mock Examination 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students