Physics
Paper 1
Instructions to candidates
- This paper consists of two sections A and B.
- Answer all the questions in the two sections in the spaces provided after each question
- All working must be clearly shown.
- Electronic calculators and Mathematical tables may be used.
- All numerical answers should be expressed in the decimal notations.
- Take g = 10m/s²
Questions
SECTION A (25 MARKS)
Answer all the questions in this section in the spaces provided.
- The reading of volume of a liquid in a burette is 37.5cm³. What is the new volume when 10 ml of the same liquid is added? (1 mk)
- A block of dimension 0.2m by 0.1m by 5cm has a mass of 500g and rests on a flat surface. Determine the least pressure that can be exerted by the block on the surface. (2mks)
- The mass of a body is constant but its weight on earth is not. Explain. (2 mks)
-
- Two samples of bromine vapour are allowed to diffuse separately under different conditions: one a vacuum and the other in air. State with reason the condition in which the bromine vapour will diffuse faster. (2 mks)
- What precautions should be taken when performing the experiment above (1 mk)
- What do you understand by the term carbon dating (1 mk)
- State and explain two factors which affect surface tension of a liquid. (2 mks)
- The uniform rod of length one metre shown in figure below is in equilibrium
Find the value of x if the weight of the rod is 40N.(3 mks)
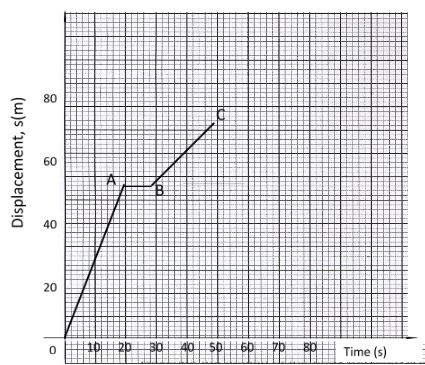
- The figure below shows the displacement- time graph for a certain body
- Describe the motion of the body between A and B (1 mk)
- Determine the velocity between OA (2 mks)
-
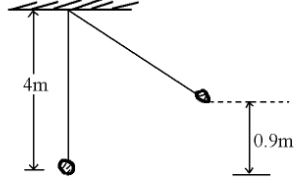
- A body of mass 20kg hangs 4m and swings through a vertical height of 0.9m as shown in the figure below.
Determine;- The potential energy at its highest position. (1 mk)
- The speed of the body when passing through the lowest point. (2 mks)
- A body of mass 20kg hangs 4m and swings through a vertical height of 0.9m as shown in the figure below.
- A crane lifts a load of 2000N through a vertical distance of 3.0m in 6 seconds.
Determine the power developed by the crane. (2 mks) - A gun of mass 10kg fires a bullet of mass 30g at a speed of 500m/s. what is the recoil velocity of the gun? (1 mk)
- The mass of an empty density bottle is x g. when full of water its mass is 70g and when full of liquid Y whose density is 0.96g/cm³ its mass is 68.4g. Determine the value of x. (density of water is 1g/cm³) (2 mks)
SECTION B (55 MARKS)
Answer all the questions in this section in the spaces provided.
-
-
- Define absolute zero temperature (1 mk)
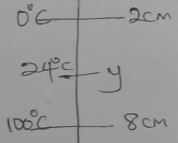
- When marking the fixed points of a thermometer, it was observed that at 0°C the mercury thread was 2cm long and at 100°C the thread was 8 cm long. Determine the length that would correspond to a temperature of 24°C. (2 mks)
- Why is steam preferred when determining the upper fixed point of a thermometer (1 mk)
- State the purpose of a constriction in a clinical thermometer (1 mk)
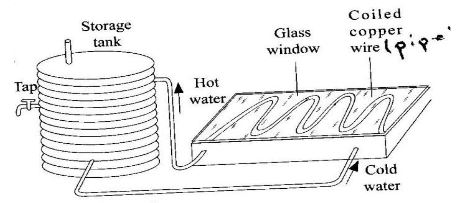
- The figure below shows a solar water system
- State the following in regard to the solar water system
- Why the pipes are made of copper (1 mk)
- Why the pipe is coiled several times (1 mk)
- Why the panel front is covered with glass (1 mk)
- Why the copper pipes are blackened (1 mk)
- What can be done to minimize heat losses as the water moves through the hot water pipe (1 mk)
- State the following in regard to the solar water system
-
-
- A particle moving along a circular path of radius 10cm describes an arc of 5cm every second. Determine
- The angular velocity (2 mks)
- Its periodic time (1 mk)
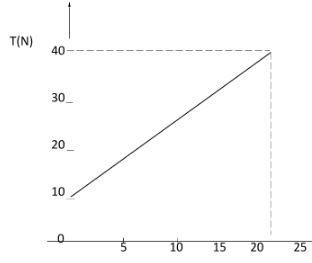
- The figure below shows a graph of tension T exerted by a stone whirled in a circle in a vertical plane using an inextensible string and moving at an increasing velocity against its angular velocity ( ⍵²) at its lowest point of rotation.
- Explain what caused the increase in tension (2 mks)
- Write an expression governing the graph (1 mk)
- Use the graph to determine:
- The mass of the stone (2 mks)
- The radius r of rotation of the stone (3 mks)
- A particle moving along a circular path of radius 10cm describes an arc of 5cm every second. Determine
-
- State Boyle’s law of gases (1 mk)
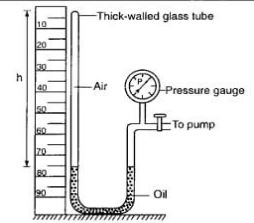
- The diagram below shows an experiment set up to investigate Boyle’s law
- State the measurements that were taken in order to verify the law (2 mks)
- Explain how the measurements can be used to verify the law ( 3 mks)
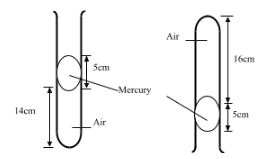
- A column of air 14 cm long is trapped by mercury thread 5cm long as shown in the figure below. When the tube is vertically inverted the air column now becomes 16cm long.
Determine the value of the atmospheric pressure in mmHg (2 mks) - In an experiment to determine the specific heat capacity of a 2.0 kg aluminium block, a potential difference of 12V is used to supply a constant current of 2A through a heater coil for 5 minutes. The block is well lagged and its temperature rises from 21°C to 37.1°C within this period. Using the values given, determine:
- The total electrical energy supplied by the heater (2 mks)
- The specific heat capacity of aluminium (2 mks)
-
- A garden sprinkler of x holes each of cross-sectional area 3.0x10-6m² and is connected to a horse-pipe of cross-sectional area of 2x10-4m². If the speed of the water in the horse pipe is 1.35 m/s, calculate;
- The mass flow rate of water in kg/s (3 mks)
- The number of holes, x if the speed of water as it emerges from the holes is 3m/s. (3 mks)
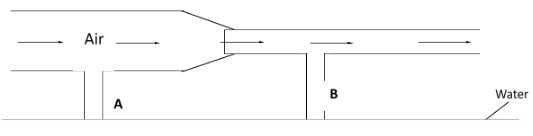
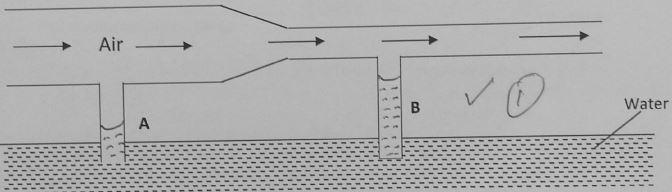
- The figure below shows air flowing through a pipe of different cross sectional areas. The two pipes A and B are dipped into water.
- Indicate on the figure the levels of water A and B (1 mk)
- Explain the cause of the difference in the levels of water in the pipes A and B (2 mks)
- Explain why a lorry loaded with bags of maize packed high up is likely to topple when negotiating a sharp bend (2 mks)
- A garden sprinkler of x holes each of cross-sectional area 3.0x10-6m² and is connected to a horse-pipe of cross-sectional area of 2x10-4m². If the speed of the water in the horse pipe is 1.35 m/s, calculate;
-
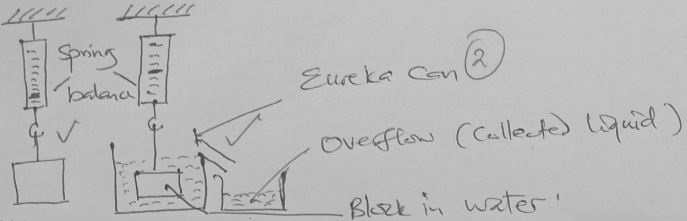
- State Archimedes’s principle (1 mk)
- You are provided with the following apparatus to carry out an experiment to verify Archimedes’s principle: a spring balance, a eureka can, a beaker, a weighing balance, water in a container and a 50g metal block
- Draw a set up showing how the apparatus are used in the experiment (2 mks)
- List down the measurements taken (3 mks)
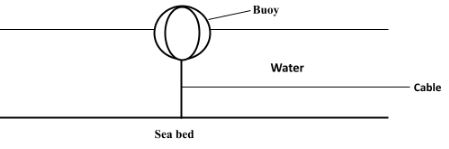
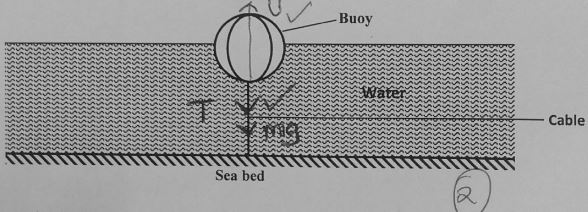
- Figure below shows a buoy of capacity 4.0x104cm³ and mass 10kg. It is held in position in sea water of density 1.04g/cm³ by a light cable fixed to the bottom so that ¾ of its volume is below the water surface.
- Indicate on the diagram the forces acting on the buoy (2mks)
- Determine the tension in the cable. (3 mks)
Marking Scheme
- New reading = 37.5cm3 - 10cm3
=27.5cm3 - Mass = 500g
= 0.5kg
Weight = (0.5 x 10) N
= 5N
Least pressure = F/Amax
= 5
(0.2 x 5) x 10-4
=50,000NM-2 - Weight varies from place to place on the earth's surface due to shape and rotation of the earth, where as the amount of matter in an object never changes.
-
- Difussion is faster in vacuum since there are no air particles to interfere with motion
- The experiment to be done in a fume chamber
- To establish the age of fossils by use of radioactive Carbon-14
- Temperature : Increase in temperature, the K.E of molecules of a liquid is increased. Intermolecular distance increase and force of cohesion is decreased hence surface tension is lowered.
Impurities: Impurities weaken cohesive forces hence reduce surface tension. - C.M = A.C.M
40 x 50 = 30( 50 + (50-x))
20000 = 30(100 - x)
2000 = 3000 - 30x
30x = 1000
x= 33.33cm -
- The body is stationary , v=0
- Δs = 50 -0 = 2.5m/s-1
Δt 20 -0
- The body is stationary , v=0
-
-
- P.E= mgh
= 20 x 10 x 0.9
=180J - K.E=P.E
1/2mv2 = 180J
v= √2 x 180/20
v=√18
=4.24ms
- P.E= mgh
-
- P=w/t
= 2000 x 3
62
=1000J/s - M1U1 + M2U2 = 0
10 + U1 + 0.03 x 500 = 0
10U1 = 15
U1 = 15/10 = 1.5
Recoil vel = 1.5ms-1 - Mw = ( 70 -x)g
Vw = (70-x)g
1gcm-3
70 - x cm3
Vw = Vol of bottle = Vy
70 - x = 68.4 - x
1 0.96
0.96(70-x) = 68.4 - x
67.2 - 0.96x = 68.4 - x
x - 0.96x = 68.4 - 67.2
0.04x = 1.2
x = 1.2/ 0.04 = 30g -
-
- The temperature at which the kinetic energy of particles is zero, and is the least temperature on kelvin scale.
-
8-2 = y-2
100 - 0 24 - 0
y-2 = 6
24 100
y= ( 6/100 x 24) + 2
= 1.44 + 2
= 3.44cm
- The temperature at which the kinetic energy of particles is zero, and is the least temperature on kelvin scale.
- It is pure, has no impurities
- To prevent backflow of liquid
-
-
- Copper is a good conductor of heat
- To increase the surface area for heat absorption
- Glass acts as a heat trap
- Black surfaces are good heat absorbers,k there increases rate of heat absorption.
- Copper is a good conductor of heat
- Lagging: covers pipes with an insulator.
-
-
-
-
- w= s/r = 0.05/0.10 = 0.5 rads-1
- T = 2Π/w = 2 x 3.142/0.5 = 12.57s
- w= s/r = 0.05/0.10 = 0.5 rads-1
-
- Increase in velocity increases centipetal force hence increasing tension.
- T= mrw2 + mg
- Increase in velocity increases centipetal force hence increasing tension.
-
- Mg = 10N
m= 10N/10ms-2
=1.0kg - Gradient = mr
30/20 = 1.5
r = gradient/m
1.5/1 = 1.5m
- Mg = 10N
-
-
-
- The pressure of a fixed mass of a gas is inversely proportional to its volume, provided the temperature is kept constant.
- The pressure of a fixed mass of a gas is inversely proportional to its volume, provided the temperature is kept constant.
-
- Volume/ height of aqir column
Pressure of the gas - Vary pressure of the gas and record corresponding volumes for a set of five values plot graph of presure against 1/volume
A staright line through origin is attained then p x 1/v
- Volume/ height of aqir column
- (Patm + 5cmHg)14 = (Patm - 5cmHg)16
14Patm + 70cmHg = 16Patm - 80cmHg
150cmHg = 2Patm
Patm = (150/2) cmHg
= 75cmHg -
- E = Ivt
= 2 x 12 x 5 x 60
= 7200J - Temperature rise ( 37.1 - 21º)C = 6.1ºC
Ivt = McΔθ
7200 = 2.0 x c x 6.1
c = 7200 = 590.2JKg-1K-1
2.0 x 6.1
- E = Ivt
-
-
-
- Vol rate= Av
= 2.0 x 10-4 x 1.35
= 2.7 x 10-4 m3/s
Mass flow rate = Vol rate x density
= 2.7 x 10-4 x 1000
= 0.27kgs-1 - R=AV
2.7 x 10-4 = 3 x 10-6 x X x 3
X = 2.7 x 10-4 = 30 holes
9 x 10-6
- Vol rate= Av
-
-
- At pipe A - low speed high pressure
At pipe B - high speed low pressure
Pressure difference ΔP is higher in B than in A hence water level at B higher than at A - Bags of maize packed high up raise the position of the c.o.g when negotiating a corner, the vertical line drawn vertically downwards from its c.o.og may fall outside the base hence the lorry topples.
-
-
-
- When an object is partialy or fully immersed in a fluid it experiences an upthrust force equal to the weight of fluid it displaces
-
-
-
- Weight of block of air
- Weight of block when partially immersed
- Weight of overflow whhen block is partially immersed
- Weight of block when fully immersed
- Weight of overflow when block is fully immersed.
-
-
-
- T + mg = U
T= U - Mg
= 4.0 x 10+4 x 10-6 x 1040 x 10 x 3 - 10 x 10
= ( 1 x 10-2 x 10400) - 100
= 104 - 100
= 4N
-
Download Physics Paper 1 Questions and Answers - Mokasa II Mock Examination 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students