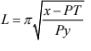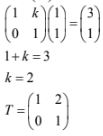MATHEMATICS
Paper 2
Instructions to Candidates
- This paper consists of two sections; Section I and Section II.
- Answer all the questions in Section I and any five questions from Section II
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

Questions
SECTION I (50 Marks)
Answer all the questions in this section in the spaces provides
- A school bursar wishes to obtain the sum of the following amounts of money paid in as school fees for three students by the CDF: Ksh 20 760, Ksh 49 105 and Ksh 17 352.The bursar estimates the sum by first rounding each of the amounts to 3 significant figures.
- Determine the estimated sum (1 mark)
- Determine the percentage error in this estimate (2 marks)
- Solve for x in : log5(3x - 2) + log5(2x - 1) = 0 without using mathematical tables or calculator. (3 marks)
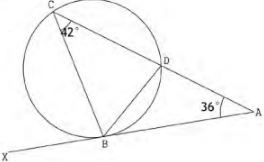
- In the figure below, ABX is a tangent. Angle CAB = 36° and angle ACB = 42°.
Calculate the size of angle BDC (2 marks) - Make P the subject of the formula in (3 marks)
- Given that 0 tan15° = 2 - √3 = − , simplify (2 marks)
1
tan15°. - Solve the equation 5cos2θ + 2 = 3sin2θ - 2cosθ for the range 0 ≤ θ ≤ 360(4 marks)
- Solve the simultaneous equation (4 marks)
2x - y =3
x2 - xy = -4 - Use binomial expansion to simplify(√2 + √5)4(√2 - √5 )4(4 marks)
- The life expectancy in hours of 40 bulbs are shown in the table below.
Calculate the quartile deviation of the life expectancy (4 marks)Expectancy
(hours)90 - 94 95 - 99 100 - 104 105 - 109 110 - 114 115 - 119 Frequency (f) 3 10 12 9 4 2 - Given that y is inversely proportional to xn and k is the constant of proportionality and that x = 2 , when y = 4½ , and x = 3, when y =11/3 . Find the values of n and k . (4 marks)
- A poultry farmer vaccinated 640 of his 700 chicken against a disease. Two months later 15% of the vaccinated and 70% of the unvaccinated chicken contracted the disease. Calculate the probability that the chicken chosen at random contracted the disease. (3 marks)
- A pilot leaves point T (60°S ,15°W ) and flies due East for a distance of 1260nm to a point U . Determine the position of U . (3 marks)
- The equation of a circle is given as 1/3x2 + 1/3y2 - 11/3x + 2y - 1=0 . Draw the circle on the grid provided. (4 marks)
- Pipes S and T can fill a tank in 2 hours and 3 hours respectively. Pipe U can empty the full tank in 4 hours. How long will it take to fill the tank with all the pipes running? (2 marks)
- Table below is part of tax table for annual income for the year 2020.
In the year 2020, the tax on Oyuga’s annual income was Ksh.37 000. Calculate Oyuga’s annual income in K£. (3 marks)Taxable income in K£ p.a. Rate in Kshs. per K£ Under K£4201 2 From K£4201 but under K£8401 3 From K£8401 but under K£12601 4 - The position vectors of points A, B and C are a, b and c respectively. Point C divides AB in the ratio 5 : 2. − Express c in terms of a and b. (2 marks)
SECTION II (50 marks)
Answer only five questions in this section in the spaces provided
- The Hire Purchase (H.P) price of a public address system was Ksh 448 000. A deposit of Ksh 112 000 was paid followed by 24 equal monthly instalments. The cash price of the public address system was 15% less than the H.P price.
- Calculate :
- The monthly instalment. (2 marks)
- The cash price. (2 marks)
- A customer decided to buy the system in cash and was allowed an 8% discount on the cash price. He took a bank loan to buy the system in cash. The bank charged compound interest on the loan at rate of 16% p.a. compounded quarterly. The loan was repaid in 12 2 years. Calculate the amount repaid to the bank by the end of the 12 2 years. (3 marks)
- Express as a percentage of the Hire Purchase price, the difference between the amounts repaid to the bank and the Hire Purchase price. (3 marks)
- Calculate :
-
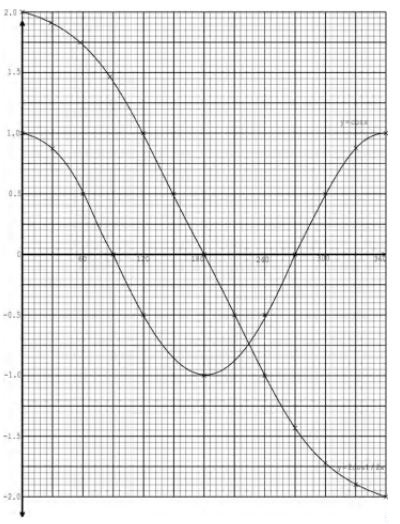
- Complete the table below for the function y= cos x° and y=2Cos½x° , for < x < 360° (2 marks)
x° 0 30 60 90 120 150 180 210 240 270 300 330 360 Cos x° 1 0.87 0.50 -0.87 -1 -0.50 0.50 1 2 Cos½ x° 2 1.93 1.41 0.52 0 -1 -1.73 -2 - On the grid provided, draw the graph of y= cos x° and y=2Cos½x° using a scale of: 1cm to represent 300 on x-axis and 4 cm to represent 1 unit on y-axis (5 marks)
- Use your graph to determine:
- The period of the function y=2Cos½x° (1 mark)
- The transformation that maps the function y= cos x° onto y=2Cos½x° (1 mark)
- The values of x for which cos½x° - ½cos x° = 0 (1 mark)
- Complete the table below for the function y= cos x° and y=2Cos½x° , for < x < 360° (2 marks)
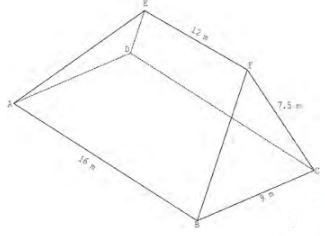
- The figure ABCDEF below represents a roof of a house. AB = DC = 16 m, BC = AD = 9 m, AE = BF = CF = DE =7.5 m and EF = 12 m.
- Calculate, correct to 4 significant figures, the perpendicular distance of EF from the plane ABCD. (3 marks)
- Calculate, correct to 2 decimal places, the angle between:
- The planes ADE and ABCD. (2 marks)
- The line AE and the plane ABCD. (2 marks)
- The planes ABFE and DCFE. (3 marks)
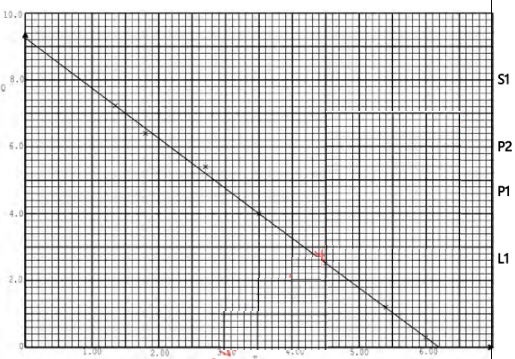
- In an experiment involving two variables T and Q , the following results were obtained.
T 0.45 1.35 1.80 2.55 3.50 4.50 5.40 6.00 Q 8.6 7.2 6.3 5.3 4.0 2.5 1.2 0.3 - On the grid provided, plot a graph of Q against T and draw the line of best fit for the data. (4 marks)
- The variables T and Q are connected by the equation Q aT b = + where a and b are constants.
Determine:- The values of a and b (3 marks)
- The equation of the line of best fit. (1 mark)
- The value of T when Q = 0 (2 marks)
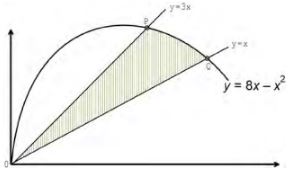
- In the figure below, the shaded region is bounded by the lines y x = 3 , y x = and the curve y xx = − 8 .The two straight lines intersect the curve at points P and Q .
- Determine the coordinates of point P and Q . (2 marks)
- Calculate the exact area of the:
- Region bounded by the curve and the line y = x . (3 marks)
- Region bounded by the curve and the line y = 3x . (3 marks)
- Shaded region. (2 marks)
- The vertices of a rectangle ABCD are A (-1,1), B(1,1), C(1,4) and D(-1,4). The vertices of its image under transformation T are A'(1,1) B'(3,1) C'(9,4) and D'(7,4).
-
- Draw on the grid provided rectangle ABCD and its image A'B'C'D' under the transformationT . (2 marks)
- Describe fully the transformationT . ( 3 marks)
- Determine the matrix of transformation T (2 marks)
- On the same grid as in (a), draw rectangle A"B"C"D" the image of rectangle ABCD under a stretch with line y =1 invariant and stretch factor 2. State the coordinates of A"B"C"D" (3 marks)
-
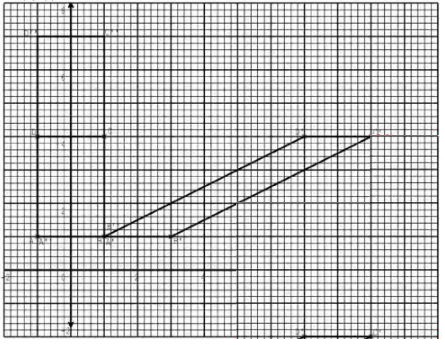
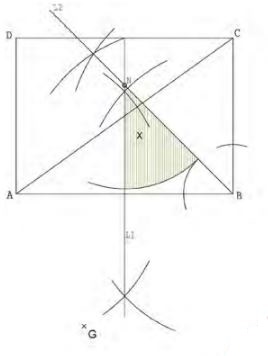
- The figure below shows a rectangle ABCD with AB = 96 m and diagonal AC = 120 m.
- Construct the locus L1 of points equidistant from A and B and locus L2 of points equidistant from BC and BA. If L1 and L2 meet at N inside the rectangle, locate point N. (3 marks)
- A point X is to be located inside the rectangle such that it is nearer B than A and also nearer AB than BC. If it is not greater than 45 m from N shade the region where the points could be located. (4 marks)
- Calculate the area of the region X (3 marks)
-
- The first term of an arithmetic progression (AP) is −11 .The sum of the first 8 terms of AP is 52.
- Find the common difference of AP. (2 marks)
- Given that the sum of the first n terms of the AP is greater than 920. Find the least value of n . (3 marks)
- The 3rd, 7th, and 17th terms of another AP form the first three terms of a geometric progression (GP). If the common difference of the AP is 3.
Find:- The first term of GP (3 marks)
- The sum of the first 7 terms of the GP. (2 marks)
- The first term of an arithmetic progression (AP) is −11 .The sum of the first 8 terms of AP is 52.

Marking Scheme
-
- 20 800 + 49 100 + 17 400 = 87 300
- % error = 87300 - 87217 x 100%
87217
8300 % or 0.09516%
87217
- 20 800 + 49 100 + 17 400 = 87 300
- Log 5(3x-2) + Log (2x-1) = 0
Log5[(3x-2)(2x-1)] = Log51
⇒6x2 - 7x + 2=1
6x2 - 7x + 1=0
(6x+1)(x-1)=0
x= -1/6 or x=1
x=1 - <ABD = 42°(Alternate segemnt theorem)
<BDC = 42° + 36° = 78° - L² = x - PT
π² Py
L²Py = xπ² - PTπ²
L²Py + PTπ² = xπ²
P = xπ²
L²y + Tπ² - 1 = 1
tan 15° 2 -√3
1(2+√3)
(2-√3)(2+√3)
2+√3
4-3
2+√3 - 5Cos2θ + 2= 3(1-Cos2θ) - 2cosθ
8Cosθ + 2Cosθ -1 = 0
(4Cosθ - 1)(2Cos θ+1)=0
cosθ =¼ or cos θ = -½
θ = 75.52°. 120°, 240°, 288.48° - x2 - x(2x-3)=-4
x2 - 2x2 + 3x=-4
x2 - 3x - 4=0
(x+1)(x-4)=0
x=-1 or x=4
y=-5 or y=5 - (√2 + √5)4 - (√2-√5)4
(√2 - √5)4 = (√2)4 + 4(√2)3(√5) + 6(√2)2(√5)2 + 4(√2)(√5)3 + (√5)4
= 4 + 8√10 x 60 + 20√10 = 25 = 89 + 28√10
(√2 - √5)4 = 4 - 8√10 + 60 - 20√10 + 25 = 89 - 28√10
(√2 + √5)4 - (√2 - √5)4 = (89 +28√10) - (89 - 28√10)
56√10 -
Q1 = 94.5 + (10 -3/10) x 5 = 98.0Cumulative frequency 3 13 25 34 38 40
Q3 = 104.5 + (30-25/9) x 5= 107.28
quartile deviation
= 107.28 - 98.0
2
= 4.639 - y = k/xn ⇒ 4½ = k/2n and 11/3 = k/3n
4½ x 2n = 11/3 x 3n
(2/3)n = (2/3)3
n=3
k= 4/3 x 27 =36 - p( contracted disease) = (⁶⁴⁰/₇₀₀ x ¹⁵/₁₀₀ ) + (⁶⁰/₇₀₀ x ⁷⁰/₁₀₀)
24/175 + 3/50
69/350 - 60θCos60° = 1260
θ= 42°
U(60°S, 27°E) - 1/3x2+1/3y2-11/3x+2y-1=0
x2-4x+4+y2+6y+9=3+4+9
(x-2)2+(y+3)2=42
Centre(2,-3) radius = 4 units - In 1h 1/2 + 1/3 - 1/4 = 7/12 is filled
time taken to fill tank k=12/7
=15/7 - 1st slab: 4200 x 2 = Ksh 8,400
2nd slab: 4200 x 3 = Ksh 12,600
3rd slab: y x 4 = (37000 - 21000)
y=4000
annual income = 4200 + 4200 + 4000 = 12400 - OC = 5/3b + -2/3a
= 5/3b - 2/3a -
-
- 448000 - 112000
24
Ksh14000 - 85 x 448000
100
Ksh 380,800
- 448000 - 112000
- 92/100 x 380800
350336 = (1 + 4/100)10
Ksh 518,582 - 518582.86 - 448000 x 100%
448000
70582.86 x 100
448000
15.76%
-
-
-
-
x° 60 90 120 210 270 330 Cos x 0.5 1 -0.5 -0.87 0 0.87 2cos½x° 1.73 1.41 1 -0.52 -1.41 -1.93 -
- Period = 720°
- Stretch along y - axis, stretch factor 2 followed by stretch along x-axis, stretch factor 2
- 225° ± 2°
-
-
- height of traingle = √7.52 - 4.52 = 6m
vertical height = √62 - 22
= 5.657m -
- Cos θ = 2/6
θ = 70.53° - Sin α = 5.657/7.5
α = 48.96° - Slant length= √7.52 - 22
=7.228m
Sin½β= 4.5/ 7.228
β= 2 x 38.50
β= 77.00°
- Cos θ = 2/6
- height of traingle = √7.52 - 4.52 = 6m
-
-
-
- a=gradient = 7.0 - 4.0
1.5 - 3.5
a= -1.5
b= y - intercept = 9.2 ± 0.1 - Q= -1.5T + 9.2
- 0=-1.5T + 9.2
1.5T=9.2
T=6.133
or when Q=0
T= x-intercept
T = 6.15 ± 0.04
- a=gradient = 7.0 - 4.0
-
-
- 8x-x2=3x
5x-x2
x(5-x)=0
x=0 or x=5
P(5,15)
8x-x2=x
7x-x2=0
x97-x)=0
x=0 or x=7
Q(7,7) -
- ∫70 (8x-x2)dx - ∫70 xdx
[4x2 - x³/3 + c]70 -[x²/2+c]70
[4 x 72 - 7³/3] - [7²/2]
812/3 - 241/2
=571/6 - ∫50 (8x-x2)dx - ∫50 3dx
[4x2 - x³/3 + c]50 -[x²/2+c]50
[4 x 52 - 5³/3] - [3 x 5²/2]
581/3 - 371/2
=205/6 - Shaded area = 571/6 - 201/6
361/3 sq units
- ∫70 (8x-x2)dx - ∫70 xdx
- 8x-x2=3x
-
-
-
- Transformation is a shear
linear x- axis in variant
point B(1,1) mapped onto point B'(3,1) -
-
- A*(-1,1), B*(1,1), C*(1,7), D*(-1,7)
-
-
-
- θ= 45 ± 1°
Area of region x = 45/360 x 22/7 x 452
=795.54m2
-
-
-
- 8/2[2x-11+(8-1)d]=52
-88+28d=52
d=5 - n/2[2x=11+(n-1)5]>920
-22n+5n2-5n>1840
5n2-27n-1840>0
n= 27 ± √(-27)2-4x5x-1840
2 x 5
n= 27 ± √37529
10
n= 22.072 or -16.672
Hence least volume of n=23 terms
- 8/2[2x-11+(8-1)d]=52
-
- a+18 = a+48
a+6 a+18
a2+36a+324 = a2 + 54a + 288
18a=36
a=2
1st term of G.P = 2+2 x 3=8 - S7 = 8(2.5⁷ ‾ ¹)
2.5 -1
S7 = 13021/12
- a+18 = a+48
-
Download Mathematics Paper 2 Questions and Answers - Maranda Mocks 2021/2022 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students