INSTRUCTIONS TO CANDIDATES
- Write your name, admission number, class and date in the spaces provided above.
- The paper consists of two sections: section I and section II.
- Section I has sixteen questions and section II has eight questions.
- Answer all the questions in section I and any five in section II.
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question
- KNEC Mathematical table and silent non-programmable calculators may be used.
For examiner’s use only
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
total |

QUESTIONS
SECTION I (50 marks)
Answer ALL the questions in this section
- Evaluate 3⁄4 + 1 5⁄7 ÷ 4⁄7 of 2 1⁄3 (3 marks)
1 3⁄7 - 5⁄8 × 2⁄15 - Simplify 4x2 - 9 (3 marks)
8x2 + 6x - 9 - Two similar solid cones made of the same material have masses of 800g and 100g respectively. If the base area of the smaller cone is 38.5cm2, calculate;
- The base area of the larger cone (2 marks)
- The radius of the larger cone (2 marks)
- Given that cos(2x)°-sin(2x-30)° = 0. Calculate the value of sin x (3 marks)
- A line L passes through point (-5, 3) and is parallel to the line y+ 1⁄2 x-5=0. Determine the equation of the line L in the y=mx+c. (3 marks)
- A Kenyan bank buys and sells foreign currency as shown in the table below.
A tourist arrived in Kenya with 15000 pounds which he converted into Kshs. at a commission of 8%. He later used half of the money before changing the balance into dollars at no commission. Calculate to the nearest dollar the amount he received. (3 marks)Buying (Kshs.)
Selling (Kshs.)
1 US dollar
95.34
95.87
1 UK pound
124.65
125.13
- Find all the integral values of x which satisfy the inequalities (3 marks)
20-x > 5+2x ≥ x+5 - A man is now three times as old as his daughter. In twelve years’ time he will be twice as old as his daughter. Find their present ages. (3 marks)
- The point P(5, 4) is mapped onto P1(9, 3) under a translation T. Find the co-ordinates of the image of Q(6, 8) under the same translation. (3 marks)
- The figure below shows a solid wedge PQRSTU. Complete the solid showing all the hidden edges with dotted lines. (3marks)
- Two machines X and Y working together can do some work in 6 days. After 2 days machine X breaks down and it takes machine Y 10 days to finish the remaining work. How long will it take machine X alone to finish the whole work if it does not break down. (3 marks)
- Solve for X in the equation. (3 marks)
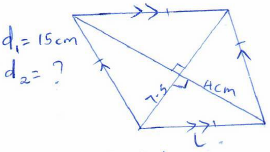
(log4X )2= 1/2 log4X+ 3/2 - The area of a rhombus is 60cm2 given that one of its diagonals is 15cm long, calculate the perimeter of the rhombus. (4 marks)
- The sum of interior angles of a regular polygon is 24 times the size of the exterior angle. Find the number of sides of the polygon and hence name it. (3 marks)
- Using tables, find the reciprocal of 0.432 and hence evaluate (√0.1225)/0.432 (3 marks)
-
- Matrices P and Q are given by P = (3 1 2)and Q =
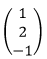 Find the product PQ. (1 mark)
Find the product PQ. (1 mark) - Given A =
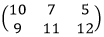 and B
and B 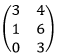 find AB (2 marks)
find AB (2 marks)
- Matrices P and Q are given by P = (3 1 2)and Q =
SECTION II (50 marks)
Answer ANY five questions in this section
- Four towns P, Q, R and S are such that Q is 160km from town P on a bearing of 065°. R is 280km on a bearing of 152° from Q. S is due west of R on a bearing of 155° from P. Using a scale of 1cm to represent 40km.
- Show the relative positions of P, Q, R and S. (6 marks)
- Find the bearing of;
- S from Q (1 mark)
- P from R (1 mark)
- Find the distance
- PS (1 mark)
- RS (1 mark)
-
- Complete the table below for the function y = 2x2 + 3x – 5. (2 marks)
x -4 -3 -2 -1 0 1 2 2x2 18 0 3x -12 -3 6 -5 y - On the grid provided draw the graph of y = 2x2 + 3x – 5 for -4 ≤ x ≤ 2 (4 marks)

- Use your graph to state the roots of
- 2x2 + 3x – 5 = 0 (1mark)
- 2x2 + 6x – 2 = 0 (3marks)
- Complete the table below for the function y = 2x2 + 3x – 5. (2 marks)
- A particle moves from rest and attains a velocity of 10m/s after two seconds it then moves with 10m/s velocity for 4 seconds. It finally decelerates uniformly and comes to rest after 6 seconds.
- Draw a velocity time graph for the motion of this particle (3 marks)
- From the graph find;
- the acceleration during the first two seconds. (2 marks)
- the uniform deceleration during the last six seconds. (2 marks)
- the total distance covered by the particle (3 marks)
-
- Find the gradient of a line L1 perpendicular to the line whose equation is y=x+4 (2 marks)
- Calculate the angle in which line L1 is making with
- x-axis (2 marks)
- y-axis (1 mark)
- Line L2 is passing through the x-axis at 2 and point T(-2, k) and it is parallel to line L1. Calculate the value of K. (2 marks)
- Another line L3 is perpendicular to line L2 and passes through point T. Calculate the equation of line L3 leaving your answer in the form ax + by + c = 0 (3 marks)
- In the figure below P, Q, R and S are points on the circle centre O. PRT and USTV are straight lines. Line UV is a tangent to the circle at S. Angle RST is 50º and angle RTV is 150º.
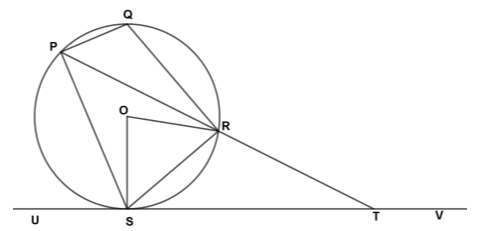
- Calculate the size of:
- angle ORS (2 marks)
- angle USP (1 mark)
- angle PQR (2 marks)
- Given that RT=7cm and ST=9cm, calculate to three significant figures:
- the length of line PR (2 marks)
- the radius of the circle. (3 marks)
- Calculate the size of:
- The figure below is triangle OAB in which OA = a and OB = b. M and N are points on OA and OB respectively such that OM:MA = 1:3 and ON:NB = 2:1.
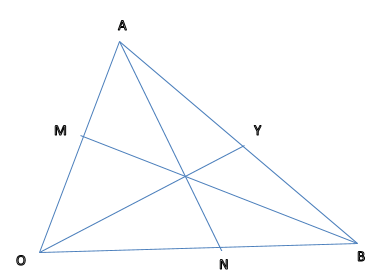
- Express the following vectors in terms of a and b
- AN (1 mark)
- BM (1 mark)
- AB (1 mark)
- Lines AN and BM intersect at X such that AX=hAN and BX=kBM. Express OX in two different ways and find the value of h and k. (6 marks)
- OX produced meets AB at Y such that AY:YB =3:2. Find AY in terms of a and b. (1 mark)
- Express the following vectors in terms of a and b
- Two circles with centres O1 and O2 have radii 10cm and 8cm respectively and intersect at points A and B. Angle AO1B = 90° and angle AO2B = 124.23°. Calculate to two decimal places;
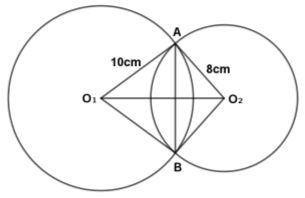
- The length AB (2 marks)
- The length O1O2 (2 marks)
- Area of minor segment centre O1 (3 marks)
- Area of quadrilateral O1AO2B (3 marks)
- PQR is a triangle with coordinates; P(3, 3), Q(5, 1) and R (2, 1). P’Q’R’ is the image of PQR under an enlargement such that the coordinates are P'(-3, 0), Q'(-7, 4) and R'(-1, 4). Using a scale of 1:1 on both axes;
-
- Plot PQR and P’Q’R’ hence locate the centre of enlargement by construction. (4 marks)
- State the scale factor of the enlargement. (2 marks)
- P’’Q’’R’’ is the image of PQR under a translation T
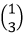 . Plot P''Q''R''. (2 marks)
. Plot P''Q''R''. (2 marks) - P’’’Q’’’R’’’ is the image of PQR under a reflection whose mirror line is y=-2. Plot P’’’Q’’’R’’ (2 marks)

-

MARKING SCHEME
SECTION I (50 marks)
Answer ALL the questions in this section
- Evaluate 3⁄4 + 1 5⁄7 ÷ 4⁄7 of 2 1⁄3 (3 marks)
1 3⁄7 - 5⁄8 × 2⁄15
Num: 3⁄4 + 1 5⁄7 ÷ 4⁄7 of 2 1⁄3
3⁄4 + 12/7 ÷ 4⁄7 × 7/3
3⁄4 + 12/7 x 3/4
=3⁄4 + 9/7 = 21 + 36
28
=57/28
Den:
= 10/7 - 5/8 x 2/15
= 80 - 35 x 2/15
56
= 45/56 x 2/15 = 3/28
∴ 57/28 ÷ 3/28 = 57/28 x 26/3 = 19 - Simplify 4x2 - 9 (3 marks)
8x2 + 6x - 9
num: (2x + 3)(2x - 3)
Den: 8x2 + 6x - 9
p = -72
s = 6
12, -6
8x2 + 12x - 6x - 9
4x(2x + 3) - 3(2x + 3)
(4x - 3)(2x + 3)
= (2x + 3)(2x - 3)
(4x - 3)(2x + 3)
= 2x - 3
4x - 3 - Two similar solid cones made of the same material have masses of 800g and 100g respectively. If the base area of the smaller cone is 38.5cm2, calculate;
- The base area of the larger cone (2 marks)
v.s.f = 800:100
=8:1
l.s.f = 3√8:1
=2:1
a.s.f = (2:1)2
=4:1
x = 38.5 x 4
=154 cm2 - The radius of the larger cone (2 marks)
πr2 = 154
r2 = 154 x 7/22
r2 = 49
r = √49
r = 7 cm
- The base area of the larger cone (2 marks)
- Given that cos(2x)°-sin(2x-30)° = 0. Calculate the value of sin x (3 marks)
cos 2x = sin (2x - 30)º
2x + 2x - 30º = 90º
4x = 120º
x= 30º
sin 30 = 0.5 or 1/2 - A line L passes through point (-5, 3) and is parallel to the line y+ 1⁄2 x-5=0. Determine the equation of the line L in the y=mx+c. (3 marks)
m1 = m2 = -1/2
y-3 = -1/2
x+5
2y - 6 = -x - 5
2y = -x + 1
y = -1/2x + 1/2 - A Kenyan bank buys and sells foreign currency as shown in the table below.
A tourist arrived in Kenya with 15000 pounds which he converted into Kshs. at a commission of 8%. He later used half of the money before changing the balance into dollars at no commission. Calculate to the nearest dollar the amount he received. (3 marks)Buying (Kshs.)
Selling (Kshs.)
1 US dollar
95.34
95.87
1 UK pound
124.65
125.13
= 15000 x 124.65 x 92/100
=1,720,170 /=
spent = 1/2 x 1,720,170
=860, 085 /=
1 → 95.87
? → 860 085
=1 x 860 085
95.87
=8971 USD - Find all the integral values of x which satisfy the inequalities (3 marks)
20-x > 5+2x ≥ x+5
20 - x > 5 + 2x
15 > 3x
5 > x or x < 5
5 + 2x ≥ x + 5
0 ≥ -x
0 ≤ x
0 ≤ x < 5
values are
0, 1 , 2 , 3/4 - A man is now three times as old as his daughter. In twelve years’ time he will be twice as old as his daughter. Find their present ages. (3 marks)
Now 12 yrs time
D-X x - 12
3x (x + 12)2
(3x + 12) = (x + 12)2
3x + 12 = 2x + 24
x = 12 yrs (daughter)
man = 3 x 12
= 36 yrs - The point P(5, 4) is mapped onto P1(9, 3) under a translation T. Find the co-ordinates of the image of Q(6, 8) under the same translation. (3 marks)
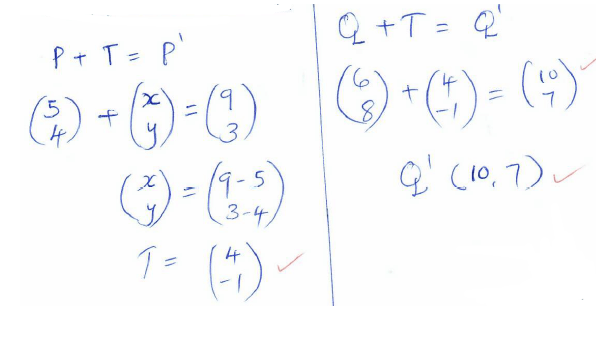
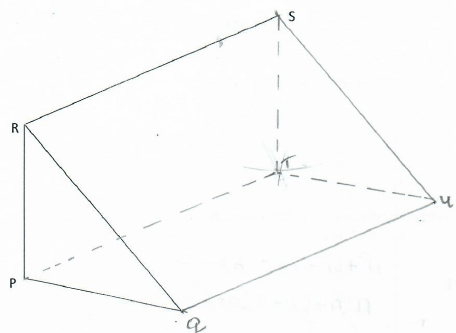
- The figure below shows a solid wedge PQRSTU. Complete the solid showing all the hidden edges with dotted lines. (3marks)
- Two machines X and Y working together can do some work in 6 days. After 2 days machine X breaks down and it takes machine Y 10 days to finish the remaining work. How long will it take machine X alone to finish the whole work if it does not break down. (3 marks)
total work by both = 6 days
work done in one day = 1/6
2 days by both = 2/6 = 1/3
remainder = 2/3
y ⇒ 10 = 2/3
alone x = 1
2/3x = 10
x = 30/2 = 15 days
∴1/15 + 1/A = 1/6
1/A = 1/6 - 1/15 = 5 + 2
30
1/A = 3/30 = 1/10
A alone = 10 days - Solve for X in the equation. (3 marks)
(log4X )2= 1/2 log4X+ 3/2
let log4X = y
y2 = 1/2y + 3/2
y2 = 1/2y + 3/2 = 0
2y2 - y - 3 = 0
p = -6 s = -1
-3 & 2
2y2 + 2y - 3y - 3 = 0
2y (y + 1) - 3(y + 1) = 0
y = -1 or 1.5(3/2)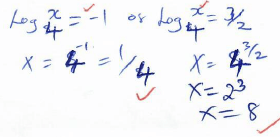
- The area of a rhombus is 60cm2 given that one of its diagonals is 15cm long, calculate the perimeter of the rhombus. (4 marks)
A = 1/2 d1d2
60 = 1/2 x 15 x d2
d2 = 8 cm
l2 = 42 + 7.52
l = √72.25
= 8.5 cm
perimeter = 4 x 8.5
= 34 cm - The sum of interior angles of a regular polygon is 24 times the size of the exterior angle. Find the number of sides of the polygon and hence name it. (3 marks)
(2n - 4) 90º = (360) 24
n
180ºn - 360º = 8640
n
180n2 - 360n - 8640 = 0
n2 - 2n - 48 = 0
p = -48
s = -2
-8, 6
n2 + 6n - 8n - 48 = 0
n(n + 6) - 8(n - 6) = 0
(n - 8) (n + 6) = 0
n = 8 or 6
8 sided (octagon) - Using tables, find the reciprocal of 0.432 and hence evaluate (√0.1225)/0.432 (3 marks)
= 1
4.32 x 101
= 2.315 x 101
= 2.315
√0.1225 = √12.25 x 10-2
= 3.4999 x 10-1
=0.34999
=0.34999 x 2.315
=0.81022685
= 0.8102 (4 s.f) -
- Matrices P and Q are given by P = (3 1 2)and Q =
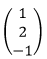 Find the product PQ. (1 mark)
Find the product PQ. (1 mark)
PQ = 3 - Given A =
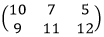 and B
and B 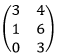 find AB (2 marks)
find AB (2 marks)
= 30 + 7 + 0 40 + 42 + 15
27 + 11+ 0 36 + 66 + 36
AB = [37 97]
[38 138]
- Matrices P and Q are given by P = (3 1 2)and Q =
SECTION II (50 marks)
Answer ANY five questions in this section
- Four towns P, Q, R and S are such that Q is 160km from town P on a bearing of 065°. R is 280km on a bearing of 152° from Q. S is due west of R on a bearing of 155° from P. Using a scale of 1cm to represent 40km.
- Show the relative positions of P, Q, R and S. (6 marks)
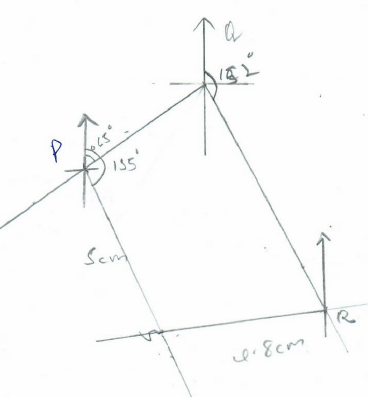
- Find the bearing of;
- S from Q (1 mark)
104º + 90º = 194 ± 1 - P from R (1 mark)
270º + 33º = 303º ± 1
- S from Q (1 mark)
- Find the distance
- PS (1 mark)
5 x 40 = 200 km ± 4 - RS (1 mark)
4.8 x 40 = 192km ± 4
- PS (1 mark)
- Show the relative positions of P, Q, R and S. (6 marks)
-
- Complete the table below for the function y = 2x2 + 3x – 5. (2 marks)
x -4 -3 -2 -1 0 1 2 2x2 32 18 8 2 0 2 8 3x -12 -9 -6 -3 0 3 6 -5 -5 -5 -5 -5 -5 -5 -5 y 15 4 -3 -6 -5 0 9 - On the grid provided draw the graph of y = 2x2 + 3x – 5 for -4 ≤ x ≤ 2 (4 marks)
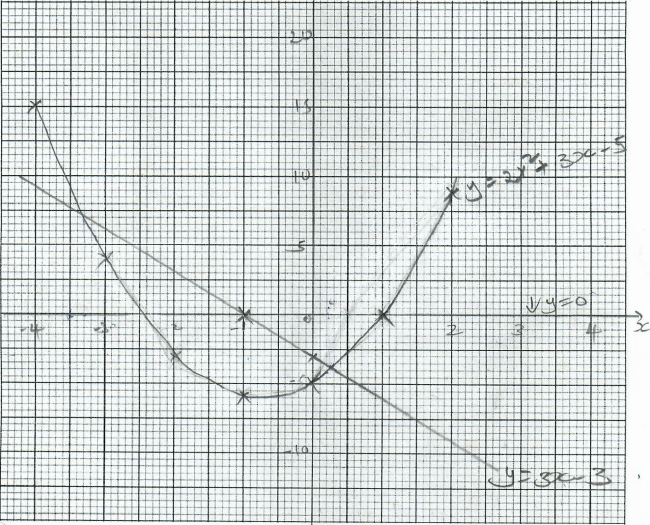
- Use your graph to state the roots of
- 2x2 + 3x – 5 = 0 (1mark)
y = 2x2 + 3x - 5
0=2x2 + 3x - 5
y = 0
x= 1 or -2 -5 - 2x2 + 6x – 2 = 0 (3marks)
y = 2x2 + 3x - 5
0 = 2x2 + 6x - 2
y = 0 - 3x - 3
x = 0.25 ± 0.1
-3.3 ± 0.1
- 2x2 + 3x – 5 = 0 (1mark)
- Complete the table below for the function y = 2x2 + 3x – 5. (2 marks)
- A particle moves from rest and attains a velocity of 10m/s after two seconds it then moves with 10m/s velocity for 4 seconds. It finally decelerates uniformly and comes to rest after 6 seconds.
- Draw a velocity time graph for the motion of this particle (3 marks)
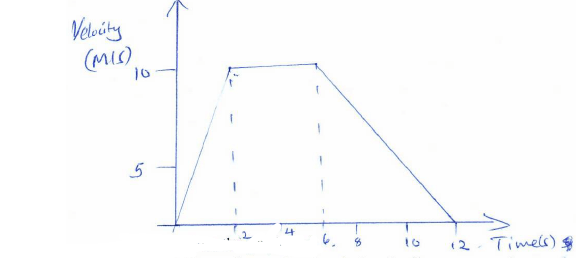
- From the graph find;
- the acceleration during the first two seconds. (2 marks)
a = Δv
Δc
= 10-0
2-0
=5m/s2 or 5ms-2 - the uniform deceleration during the last six seconds. (2 marks)
= 0 - 10
12 - 6
= -10
6
= -12/5 m/s
=-1.40 m/s2 - the total distance covered by the particle (3 marks)
D = (1/2 x 2 x 10) + (10 x 4) + (1/2 x 6 x 10)
=10m + 40m + 30m
=80m
- the acceleration during the first two seconds. (2 marks)
- Draw a velocity time graph for the motion of this particle (3 marks)
-
- Find the gradient of a line L1 perpendicular to the line whose equation is y=x+4 (2 marks)
m1m2 = -1
m1 = 1
∴m2 = -1 - Calculate the angle in which line L1 is making with
- x-axis (2 marks)
θ = Tan-1 m2 = Tan-11
= 45º - y-axis (1 mark)
θ = 45º
Alternative angles are equal
- x-axis (2 marks)
- Line L2 is passing through the x-axis at 2 and point T(-2, k) and it is parallel to line L1. Calculate the value of K. (2 marks)
through points (2,0) & (-2, k)
k - 0 = 1
-2 -2
k = -1 (-4)
k = 4
∴T(-2, 4) - Another line L3 is perpendicular to line L2 and passes through point T. Calculate the equation of line L3 leaving your answer in the form ax + by + c = 0 (3 marks)
m = 1 T= (-2, 4)
y - 4 = 1
x + 2
y - 4 = x + 2
y - x - 6 = 0
- Find the gradient of a line L1 perpendicular to the line whose equation is y=x+4 (2 marks)
- In the figure below P, Q, R and S are points on the circle centre O. PRT and USTV are straight lines. Line UV is a tangent to the circle at S. Angle RST is 50º and angle RTV is 150º.
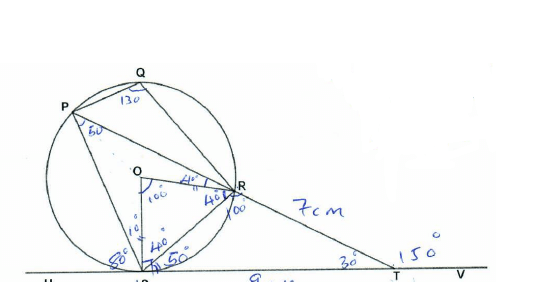
*no need to wait for the reasons
*inspect the diagram- Calculate the size of:
- angle ORS (2 marks)
40º - base angles of an isoceles Δ - angle USP (1 mark)
80º - angles in a straight line add up 180º - angle PQR (2 marks)
130º opposite angles of a cyclic quadrilateral add up to 180º
- angle ORS (2 marks)
- Given that RT=7cm and ST=9cm, calculate to three significant figures:
- the length of line PR (2 marks)
PT:RT = ST2
7(X + 7) = 92
7X = 81 - 49
X = 32/7 = 4.57CM - the radius of the circle. (3 marks)

2R = 4.57
sin 50º
2R = 4.64
R = 4.64
2
R = 2.32 cm
- the length of line PR (2 marks)
- Calculate the size of:
- The figure below is triangle OAB in which OA = a and OB = b. M and N are points on OA and OB respectively such that OM:MA = 1:3 and ON:NB = 2:1.
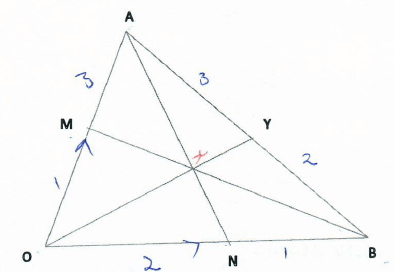
- Express the following vectors in terms of a and b
- AN (1 mark)
- BM (1 mark)
- AB (1 mark)
- Lines AN and BM intersect at X such that AX=hAN and BX=kBM. Express OX in two different ways and find the value of h and k. (6 marks)
- OX produced meets AB at Y such that AY:YB =3:2. Find AY in terms of a and b. (1 mark)
AY = 3/5 (b - a) or 3/5 b - 3/5a
- Express the following vectors in terms of a and b
- Two circles with centres O1 and O2 have radii 10cm and 8cm respectively and intersect at points A and B. Angle AO1B = 90° and angle AO2B = 124.23°. Calculate to two decimal places;

- The length AB (2 marks)
AB = 2 x 10 x sin 45º
=14.14cm
or
2 x 8 x sin 62.115º
=14.14 cm - The length O1O2 (2 marks)
O1O2 =(10 x cos 45º) + (8 x cos 62.115º)
=7.071 + 3.741
=10.812
=10.81cm - Area of minor segment centre O1 (3 marks)
= 28.57cm2 - Area of quadrilateral O1AO2B (3 marks)
=76.46cm2
- The length AB (2 marks)
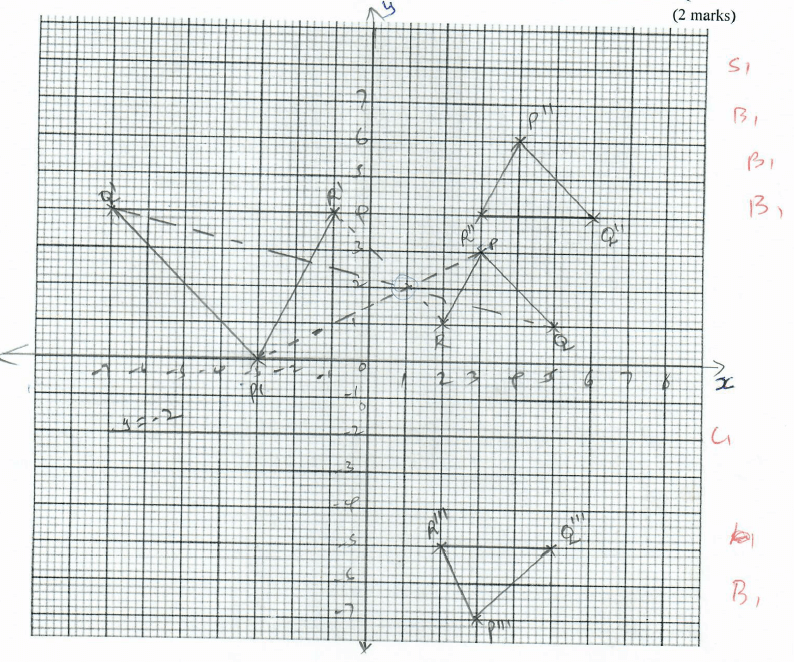
- PQR is a triangle with coordinates; P(3, 3), Q(5, 1) and R (2, 1). P’Q’R’ is the image of PQR under an enlargement such that the coordinates are P'(-3, 0), Q'(-7, 4) and R'(-1, 4). Using a scale of 1:1 on both axes;
-
- Plot PQR and P’Q’R’ hence locate the centre of enlargement by construction. (4 marks)
(1,2) - State the scale factor of the enlargement. (2 marks)
(-2)
- Plot PQR and P’Q’R’ hence locate the centre of enlargement by construction. (4 marks)
- P’’Q’’R’’ is the image of PQR under a translation T
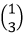 . Plot P''Q''R''. (2 marks)
. Plot P''Q''R''. (2 marks)
=( 4 3 6 )
(6 4 4) - P’’’Q’’’R’’’ is the image of PQR under a reflection whose mirror line is y=-2. Plot P’’’Q’’’R’’ (2 marks)
-
Download Mathematics Paper 1 Questions and Answers - Kigumo Mocks 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students