Mathematics Paper 2 Questions and Answers - Kigumo Mocks 2021 Exams

INSTRUCTIONS TO CANDIDATES

This paper consists of TWO sections: Section I and Section II.
Answer ALL the questions in Section I and any five questions from Section II.
Answers and working must be written on the question paper in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise

FOR EXAMINER’S USE ONLYSECTION I

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	TOTAL

SECTION II GRAND TOTAL

17	18	19	20	21	22	23	24	TOTAL

QUESTIONS

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

Evaluate without using tables or calculators. (3 marks)
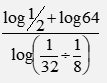
Make w the subject of the formulae. 2x = 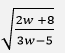(3marks)
Two pipes, P and Q can fill an empty tank in 3 hours and 4 hours respectively. It takes 5 hours to fill the tank when an outlet pipe R is opened the same time with the inlet pipes. Calculate the time pipe R takes to empty the tank. (3 marks)
Given that OM=i – 3j + 4k, ON= 6i + 3j – 5k and OQ = 2OM + 5ON, find the magnitude of OQ to 3 significant figures. (3 marks)
A triangle ABC is such that a =14.30 cm, b =16.50 cm and B =56º. Find the radius of a circle that circumscribes the triangle. (3 marks)
The third and sixth terms of a geometric progression (G.P.) are -64 and 8 respectively. Find;
1. The common ratio, (2marks)
2. The first term of the G.P. (1mark)
Calculate the standard deviation of the set of numbers
29. 31, 28, 29, 31. 46, 39, 31, (3 marks)
Grace deposited Ksh 16 000 in a bank that paid simple interest at the rate of 14% per annum. Joyce deposited the same amount of money as Grace in another bank that paid compound interest semi- annually. After 4 years, they had equal amounts of money in the banks.
Determine the compound interest rate per annum, to I decimal place, for Joyce’s deposit.(3 marks)
Simplify 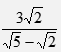, leaving the answer in the form a + b√c , where a, b and c are rational numbers (3 marks)
The table below shows income tax rates in a certain year.

Mo Monthly income in Ksh

Tax r Rate in each Ksh

1 – 9680

10%

9681 – 18800

15%

18801 – 27920

20%

27921 – 37040

25%

Over 37040

30%

In that year, a monthly personal tax relief of Ksh. 1056 was allowed. If the monthly income tax paid by an employee was Ksh 4249 calculate his monthly taxable income. (3 marks)
Grade I coffee cost sh 500 per kilogram while grade II coffee costs sh 400 per kilogram. The grades are mixed to obtain a mixture that costs sh 420 per kilogram. In what ratio should the two grades be mixed? (3 marks)
The base length and height of parallelogram were measured as 8.4 cm and 4.5 cm respectively. Calculate the percentage error in the area of the parallelogram. (3 marks)
The equation of a circle is x² +y² + 6x — 14y + 58 =r² If the circle passes through the point (2, 7). Determine its radius and the coordinates of it centre. (4 marks)
Find the gradient of the curve y = x2 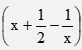at point 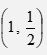(3marks)
In the figure below, the tangent HXY meets chord PQ produced at Y. Chord XZ passes through the centre, O, of the circle and intersects PQ at T. Line XY = 16 cm and QY = 10 cm.
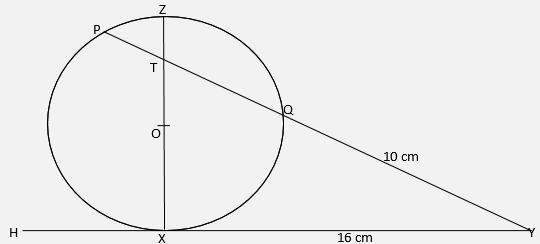
1. Calculate the length PQ. (2 marks)
2. If ZT = 4 cm and PT: TQ = 3:5, find XT. (2 marks)
Quantity P varies partly as Q and partly varies inversely as square of Q. When Q = 1, P = 1 and when Q = ½, P = -3. Find the equation of the relationship connecting P and Q. (3 marks)

SECTION II (50 Marks)
Answer any five questions from this section.

A certain Sub-county advertised for a tender to construct its headquarters. Two contractors A and B assessed the work. Contractor A indicated would do the same work in 12 months while contractor B indicated would do the same work in 18 months. The two contractors were awarded the tender. Contractor B did the work for three months then it was joined by contractor A.
1. Determine;
  1. The fraction of the work done by contractor B in 3 months, (2 marks)
  2. How long the two contractors took to complete the remaining work. (4 marks)
2. Given that contractors A and B would incur expenditure amounting to sh 120 000 per month and sh 90 000 per month respectively, calculate the total expenditure of each contractor. (4 marks)
An examination involves a written test and a practical test. The probability that a candidate passes the written test is 6/11 if the candidate passes the written test, then the probability of passing the practical test is 3/5, otherwise it would be 2/7
1. Illustrate this information on a tree diagram. (2marks)
2. Determine the probability that a candidate is awarded
  1. Credit for passing both tests. (2marks)
  2. Pass for passing the written test. (2marks)
  3. Retake for passing one test. (2marks)
  4. Fail for not passing the written test. (2marks)
1. Construct triangle PQR with PQ = 7.2cm, QR = 6.5cm and angle PQR = 480 (3marks)
2. The locus L1, of points equidistant from P and Q, and locus , L2 of points equidistant from P and R, meet at M. Locate M and measure QM (4marks)
3. A point x moves within triangle PQR such that QX ≥ QM. Shade and label the locus of X. (3marks)
The figure below shows a square ABCD point V is vertically above middle of the base ABCD. AB = 10cm and VC = 13cm.

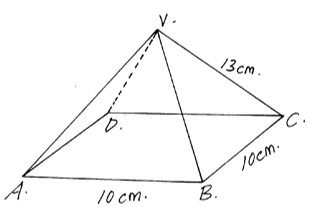
Find;
1. The length of diagonal AC (2marks)
2. The height of the pyramid (2marks)
3. The acute angle between VB and base ABCD. (2marks)
4. The acute angle between BVA and ABCD. (2marks)
5. The angle between AVB and DVC. (2marks)
The table below shows the distribution of ages in years of 50 adults who attended a clinic:-

Age

21-30

31-40

41-50

51-60

61-70

71-80

Frequency

15

11

17

4

2

1
1. State the median class (1 mark)
2. Using a working mean of 45.5, calculate:-
  1. The mean age (3 marks)
  2. The standard deviation (3 marks)
  3. Calculate the 6th decile. (3 marks)
An aircraft leaves A(60ºN,13ºW) at 1300 hours and arrives at B(60ºN, 47ºE) at 1700 hrs
1. Calculate the average speed of the aircraft in knots. (3marks)
2. Town C (60ºN, 133ºW)has a helipad. Two helicopters S and T leaves B at the same time. S moves due West to C while T moves due North to C. If the two helicopters are moving at 600 knots.
  1. The time taken by S to reach C (2marks)
  2. The time taken by T to reach C (2marks)
3. The local time at a town D (23ºN, 5ºW) is 1000 hours. What is the local time at B.? (3marks)
A certain uniform supplier is required to supply two types of shirts: one for girls labelled G and the other for boys labelled B. The total number of shirts must not be more than 400.He has to supply more of type G than of type B. However the number of type G shirts must not be more than 300 and the number of type B shirts must not be less than 80. By taking x to be the number of type G shirts and y the number of type B shirts,
1. Write down in terms of x and y all the inequalities representing the information above. (3 marks)
2. On the grid provided draw the inequalities and shade the unwanted regions. (4marks)
3. Given that type G costs Shs. 500 per shirt and type B costs Shs. 300 per shirt.
  1. Use the graph in (b) above to determine the number of shirts of each type that should be made to maximize profit. (1mark)
  2. Calculate the maximum possible profit. (2marks)
A transformation represented by the matrix 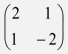maps the points A(0, 0), B(2, 0), C(2, 3) and D(0, 3) of the quad ABCD onto A¹B¹C¹D¹ respectively.
1. Draw the quadrilateral ABCD and its image A¹B¹C¹D¹. (3marks)
2. Hence or otherwise determine the area of A¹B¹C¹D¹. (2 marks)
3. Another transformation 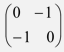maps A¹B¹C¹D¹ onto A¹¹B¹¹C¹¹D¹¹.
  Draw the image A¹¹B¹¹C¹¹D¹¹. (2mks)
4. Determine the single matrix which maps A¹¹B¹¹C¹¹D¹¹ back to ABCD. (3mks)

MARKING SCHEME

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

Evaluate without using tables or calculators. (3 marks)

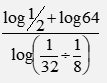
log (1/2 x 64)
log (1/32 x 8/1)
log 32
log ¹/₄
log 2⁵
log 2^-2
5 = -2¹/₂
-2
Make w the subject of the formulae. 2x = 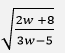(3marks)
(2x)² = 2w + 8
3w -5
4x²(3w - 5) = 2w + 8
12x²w - 20x² = 2w + 8
12x²w - 2w = 8 + 20x²
w(12x² - 2) = 8 + 20x²
w = 8 + 20x²
12x² - 2
or
w = -8 - 20x²
2 - 12x²
Two pipes, P and Q can fill an empty tank in 3 hours and 4 hours respectively. It takes 5 hours to fill the tank when an outlet pipe R is opened the same time with the inlet pipes. Calculate the time pipe R takes to empty the tank. (3 marks)
p = 3 hrs
q = 4 hrs
r = x hrs
1 w hr part of the tank filled
1 hr = (1/3 + 1/4) - 1/x = 7/12 - 1/x
⇒7x - 12 = 1
12x 5
5(7x - 12) = 12x
35x - 60 = 12x
35x - 12x = 60
23x = 60
x = 60/23 hrs or 2 ¹⁴/₂₃ hrs
Given that OM=i – 3j + 4k, ON= 6i + 3j – 5k and OQ = 2OM + 5ON, find the magnitude of OQ to 3 significant figures. (3 marks)
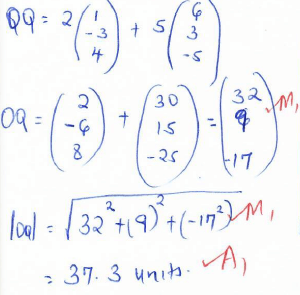
A triangle ABC is such that a =14.30 cm, b =16.50 cm and B =56º. Find the radius of a circle that circumscribes the triangle. (3 marks)

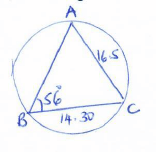
b = 2R
sin B
16.5 = 2R
sin 56
19.90:2R
2 2
9.95cm = R
The third and sixth terms of a geometric progression (G.P.) are -64 and 8 respectively. Find;
1. The common ratio, (2marks)
  ar² = -64
  ar⁵ = 8
  ar²(r³) = 8
  -64(r³) = 8
  -64 -64
  r = -1/2
2. The first term of the G.P. (1mark)
  a = -256
Calculate the standard deviation of the set of numbers
29. 31, 28, 29, 31. 46, 39, 31, (3 marks)

d = x - 33 d²

28 -5 25

29 -4 16

29 -4 16

31 -2 8

31 -2 8

31 -2 8

39 6 36

46 13 169

sd = √Σd²
n
= √286
8
= 5.979
28 + 29 + 29 + 31 + 31 + 31 + 39 + 46
8
x = 264 = 33
8
Grace deposited Ksh 16 000 in a bank that paid simple interest at the rate of 14% per annum. Joyce deposited the same amount of money as Grace in another bank that paid compound interest semi- annually. After 4 years, they had equal amounts of money in the banks.
Determine the compound interest rate per annum, to I decimal place, for Joyce’s deposit.(3 marks)
total amount for Grace in 4 years
16000 x 14/100 x 4 = 8960
16000 + 8960 = 24960

Joyce
A = P(1 + r/100)ⁿ
24960 = 1600 (1 + (r/2)/100)8
1.56 = (1 + r/200)8
1.0572 = 1 + r/200
0.0572 = ^r/₂₀₀
11.4% = r
Simplify 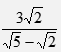, leaving the answer in the form a + b√c , where a, b and c are rational numbers (3 marks)
ans = 2 + √10
The table below shows income tax rates in a certain year.

Mo Monthly income in Ksh

Tax r Rate in each Ksh

1 – 9680

10%

9681 – 18800

15%

18801 – 27920

20%

27921 – 37040

25%

Over 37040

30%

In that year, a monthly personal tax relief of Ksh. 1056 was allowed. If the monthly income tax paid by an employee was Ksh 4249 calculate his monthly taxable income. (3 marks)
gross tax = 4249
+ 1056
5304
9680 x 10/100 = 968
9120 x x15/100 = 1368
9120 x 20/100 = 1824
x × 25/100 = 1144
x = 1144 x 100 = 4576
25
taxable income = 32,496 /=
Grade I coffee cost sh 500 per kilogram while grade II coffee costs sh 400 per kilogram. The grades are mixed to obtain a mixture that costs sh 420 per kilogram. In what ratio should the two grades be mixed? (3 marks)
500x + 400y = 420
x + y
500x + 400y = 420x + 420y
500x - 420x = 420y - 400y
80x = 20y
20y 20y
x = 1
y 4
x:y = 1:4
The base length and height of parallelogram were measured as 8.4 cm and 4.5 cm respectively. Calculate the percentage error in the area of the parallelogram. (3 marks)
A = b x h
max area = 8.45 x 4.55
=38.4475
min area = 8.35 x 4.45
=37.1575
A.E = 38.4475 - 37.1575
2
=0.645
P.E = 0.645 x 100
37.8
= 1.706%
The equation of a circle is x² +y² + 6x — 14y + 58 =r² If the circle passes through the point (2, 7). Determine its radius and the coordinates of it centre. (4 marks)
2² + 7² + 6[2] - 14(7) + 58 = r2
4 + 49 + 12 - 98 + 58 = r²
25 = r²
5 = r
x² + y² + 6x - 14y + 58 = 25
x² + 6x + 9 + y² - 14y + 49 = 33 + 9 + 49
(x + 3)² + (y - 7)² = 25
centre (-3, 7)
r = 5
Find the gradient of the curve y = x2 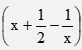at point 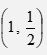(3marks)
y = x³ + 1/2x² - x
dy/dx = 3x² + x - 1
= 3(1²) + (1) - 1
=3 + 1 - 1
= 3
In the figure below, the tangent HXY meets chord PQ produced at Y. Chord XZ passes through the centre, O, of the circle and intersects PQ at T. Line XY = 16 cm and QY = 10 cm.
1. Calculate the length PQ. (2 marks)
  let PQ = y
  (10 + y)10 = 16
  100 + 10y = 256
  10y = 156
  y = 15.6 cm
  PQ = 15.6cm
2. If ZT = 4 cm and PT: TQ = 3:5, find XT. (2 marks)
  PQ = 15.6
  PT = 3/8 x 15.6
  =5.85
  TQ= 5/8 x 15.6
  =9.75cm
  PT x TQ = ZT.TX
  5.85 x 9.75 = 4 x x
  x = 5.85 x 9.75
  4
  = 14.26cm
Quantity P varies partly as Q and partly varies inversely as square of Q. When Q = 1, P = 1 and when Q = ½, P = -3. Find the equation of the relationship connecting P and Q. (3 marks)
ans = P = Q - ¹/_Q²

SECTION II (50 Marks)
Answer any five questions from this section.

A certain Sub-county advertised for a tender to construct its headquarters. Two contractors A and B assessed the work. Contractor A indicated would do the same work in 12 months while contractor B indicated would do the same work in 18 months. The two contractors were awarded the tender. Contractor B did the work for three months then it was joined by contractor A.
1. Determine;
  1. The fraction of the work done by contractor B in 3 months, (2 marks)
    A = 12m
    B = 18m
    1 month = 1/18
    3 months - ?
    1/18 x 3
    = ¹/₆th of the week
  2. How long the two contractors took to complete the remaining work. (4 marks)
    remaining week
    1 - 1/6 = 5/6
    both working
    1 month = 1/18 + 1/12
    2 + 3 = 5
    36 36
    5/36 → 1 month
    5/6→?
    = 6 months
2. Given that contractors A and B would incur expenditure amounting to sh 120 000 per month and sh 90 000 per month respectively, calculate the total expenditure of each contractor. (4 marks)
  total months for B
  3 + 6 = 9 months
  9 x 90000 = 810 000/=
  total months for A
  6 months
  6 x 120 000 = 720 000
An examination involves a written test and a practical test. The probability that a candidate passes the written test is 6/11 if the candidate passes the written test, then the probability of passing the practical test is 3/5, otherwise it would be 2/7
1. Illustrate this information on a tree diagram. (2marks)
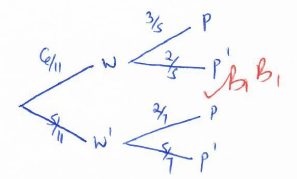
2. Determine the probability that a candidate is awarded
  1. Credit for passing both tests. (2marks)
    p(w and p)
    p = 6/11 x 3/5 = 18/55
  2. Pass for passing the written test. (2marks)
    p(w and p) or p(w and p¹)
    (6/11 x 3/5) + (6/11 x 2/5)
    18/55 + 12/55 = 30/55
  3. Retake for passing one test. (2marks)
    p(w and p¹) or p(w¹ and p¹)
    (6/11 x 2/5) + (5/11 x 2/7)
    12/55 + 10/77 = 134/385
  4. Fail for not passing the written test. (2marks)
    p(w¹ and p¹)
    5/11 x 2/7 = 10/77
1. Construct triangle PQR with PQ = 7.2cm, QR = 6.5cm and angle PQR = 480 (3marks)
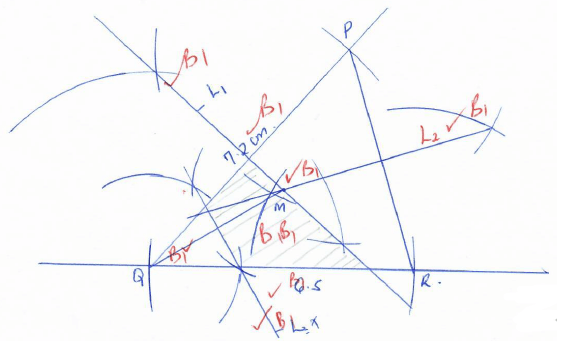
2. The locus L1, of points equidistant from P and Q, and locus , L2 of points equidistant from P and R, meet at M. Locate M and measure QM (4marks)
  QM = 3.8 ±0.1 cm
3. A point x moves within triangle PQR such that QX ≥ QM. Shade and label the locus of X. (3marks)
The figure below shows a square ABCD point V is vertically above middle of the base ABCD. AB = 10cm and VC = 13cm.

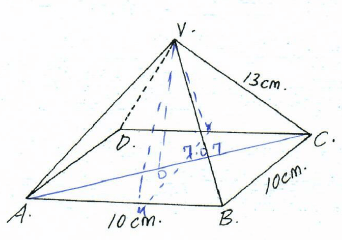
Find;
1. The length of diagonal AC (2marks)
  AC = √10² + 10²
  Ac = 14.14cm
2. The height of the pyramid (2marks)
  
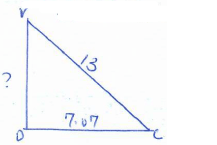
  √13² - 7.07²
  =10.91cm
3. The acute angle between VB and base ABCD. (2marks)
  
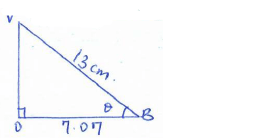
  cos Φ = A
  H
  =7.07
  13
  cos Φ = 0.5438º
  Φ = 57.05º
4. The acute angle between BVA and ABCD. (2marks)
  
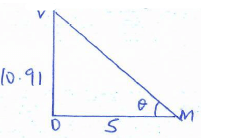
  Tan θ = 0/A
  = 10.91
  5
  =65.39º
5. The angle between AVB and DVC. (2marks)
  
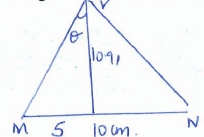
  ∠ mvn
  Tan θ = o/A
  = 5/10.91
  θ = 24.62 x 2
  = 49.24º

The table below shows the distribution of ages in years of 50 adults who attended a clinic:-

Age	21-30	31-40	41-50	51-60	61-70	71-80
Frequency	15	11	17	4	2	1

State the median class (1 mark)
41-50

Using a working mean of 45.5, calculate:-

class	mid-point x	x - 45.5	f	xf	d²f	c.f
21-30	25.5	-20	15	-300	6000	15
31-40	35.5	-10	11	-110	1100	26
41-50	45.5	0	17	00	0000	43
51-60	55.5	10	4	40	400	47
61-70	65.5	20	2	40	800	49
71-80	75.5	30	1	30	900	50
			Σf = 50	Σxf = -300	Σd2f = 9200

The mean age (3 marks)
mean(x) = 45.5 + -300
50
= 45.5 - 6
= 39.5
The standard deviation (3 marks)
ans = 12.17
Calculate the 6th decile. (3 marks)
6th decile = 6/10 x 50 = 30
= 40.5 + (30 - 26)10
17
=40.5 + 2.353
=42.853

An aircraft leaves A(60ºN,13ºW) at 1300 hours and arrives at B(60ºN, 47ºE) at 1700 hrs
1. Calculate the average speed of the aircraft in knots. (3marks)
  
  angle at the centre = (13 + 47) = 50
  1 = 60 cos
  distance between A & B = 50 x 60 cos 60 = 1500n.m
  time taken 1700hrs - 1300hrs = 4 hrs
  speed = 1500 = 375knots
  4
2. Town C (60ºN, 133ºW)has a helipad. Two helicopters S and T leaves B at the same time. S moves due West to C while T moves due North to C. If the two helicopters are moving at 600 knots.
  1. The time taken by S to reach C (2marks)
    distance from B to C for S = 180 x 60 x cos 60 = 5400 n.m
    distance for B to C for T = 60 x 60 = 3600n.m
    time taken by s = 5400 = 9 hrs
    600
  2. The time taken by T to reach C (2marks)
    time taken by T = 3600 = 6hrs
    600
3. The local time at a town D (23ºN, 5ºW) is 1000 hours. What is the local time at B.? (3marks)
  1 = 4 min
  diff in longitude (5 + 47) = 52
  52 x 4 = 208m
  =3hrs 28min
  local time at B = 1000hrs + 3 hrs 28 min
  =1328 hrs
A certain uniform supplier is required to supply two types of shirts: one for girls labelled G and the other for boys labelled B. The total number of shirts must not be more than 400.He has to supply more of type G than of type B. However the number of type G shirts must not be more than 300 and the number of type B shirts must not be less than 80. By taking x to be the number of type G shirts and y the number of type B shirts,
1. Write down in terms of x and y all the inequalities representing the information above. (3 marks)
  girls = G = x
  Boys = B= y
  1. G + B ≤ 400
  2. G>B
  3. G≤300
  4. B>80
  5. x + y ≤ 400
  6. x > y
  7. x ≤ 300
  8. y > 80
  9. x ≥ 0
  10. y ≥ 0
2. On the grid provided draw the inequalities and shade the unwanted regions. (4marks)
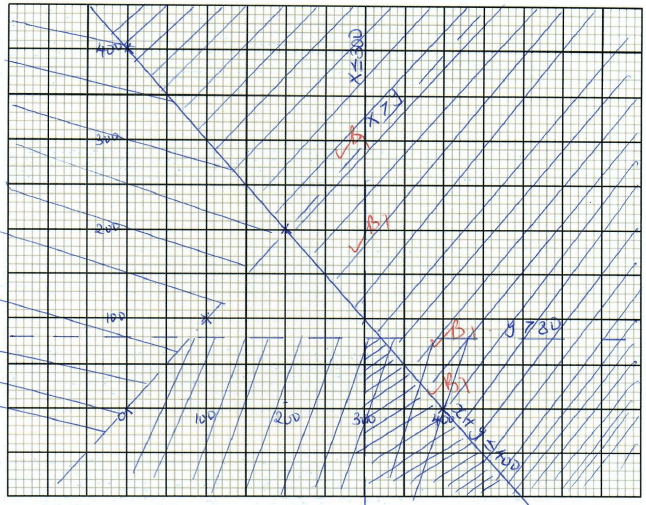
3. Given that type G costs Shs. 500 per shirt and type B costs Shs. 300 per shirt.
  1. Use the graph in (b) above to determine the number of shirts of each type that should be made to maximize profit. (1mark)
    (300,100)
    300 - G
    100 - B
  2. Calculate the maximum possible profit. (2marks)
    500(300) + 300(100)
    150 000 + 30 000
    = 180 000
A transformation represented by the matrix 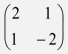maps the points A(0, 0), B(2, 0), C(2, 3) and D(0, 3) of the quad ABCD onto A¹B¹C¹D¹ respectively.
1. Draw the quadrilateral ABCD and its image A¹B¹C¹D¹. (3marks)
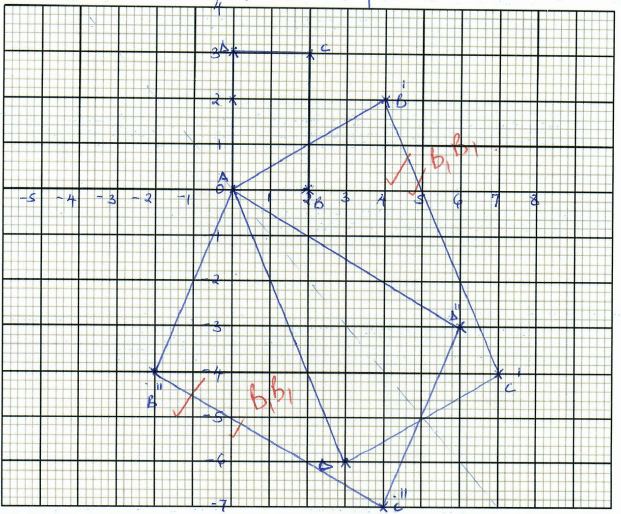
2. Hence or otherwise determine the area of A¹B¹C¹D¹. (2 marks)
3. Another transformation 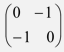maps A¹B¹C¹D¹ onto A¹¹B¹¹C¹¹D¹¹.
  Draw the image A¹¹B¹¹C¹¹D¹¹. (2mks)
4. Determine the single matrix which maps A¹¹B¹¹C¹¹D¹¹ back to ABCD. (3mks)