Mathematics Paper 1 Questions and Answers - Nyeri Mocks 2021 Exams

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Nyeri Mocks 2021 Exams

Download PDF for future reference Get on Whatsapp for 50/-

Instructions to candidates

This paper consists of two sections: Section I and Section II.
Answer all the questions in Section I and only ﬁve questions from Section II.
Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION 1 (50 marks) Answer all questions in this section

Simplify without using a calculator. (3marks)
1⁴/₅ of ²⁵/₁₈ ÷ 1²/₃ × 24
2¹/₃ − ¼ of 12 ÷ ⁵/₃
Find the size of each interior angle of a regular pentagon. (3marks)
Find all the integral values of x which satisfy the inequalities. (3marks)
x + 8 > 4x –6 ≥ 3(4 –x)
Three types of tea A, B and C are mixed in the ratio 2:3:5 by mass. Type A, B and C tea cost Ksh210, Ksh160 and Ksh120 respectively per kilogram. The blend is to be sold at a 30% profit. Determine the selling price of the blend per kilogram. (3marks)
Determine the radius of a uniform cylindrical block 1.4m long and of density of 2.2g/cm³ if the mass is 47432g (π=²²/₇) (3marks)
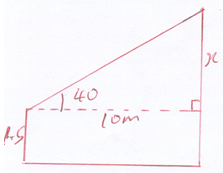
A boy whose height is 1.5 stands on the horizontal ground and observes that the top of flag pole, 10m away, makes angle of elevation of 40°. Calculate the height of the flag post. (3marks)
Two similar cylinders have total surface areas of 45cm² and 20cm². If the larger has a mass of 81g . Find the mass of the smaller one. (3marks)
Find the values of x and y in (4marks)
2^{3x +y} x 3^4x–y = 648
Simplify the following expression. (3marks)
3x² – 14xy – 5y²
3x² – 75y²
Use tables of reciprocals and cubes to evaluate to four significant figures. (3marks)
3 − 2
0.375³ 981.7
On Saturday October 15, 2017 the following were the buying and selling prices of foreign currencies in a certain bank.

Buying(Ksh) Selling(Ksh)

1 Euro 111.53 112.01

100 Japanese Yen 97.32 97.70

A Japanese travelling from Sweden arrived in Kenya with X Euros. He converted all the X Euros to Kenya shillings at the bank while in Kenya he spent a total of kenya shillings 350000 and then converted the remaining Kenya shillings to Japanese Yen at the same bank at the same rates. If the Japanese received 32669396 Yen. Calculate the value of X. (3marks)
The GCD is 1620, 1800 and a third number is 180. The LCM of the three numbers is 8100. Find the difference between greatest and smallest possible third number. (3marks)
The position vectors of points A and B are and respectively, point C divides AB externally in the ratio 5:2. Find the position vector of C. (3marks)
The average mark scored by the first 27 students in a mathematics test is 52. The average mark scored by the remaining 37 is 58. Calculate the mean mark for the whole class. (3marks)
Five years ago, a mother’s age was four times that of the daughter. In four years to come, she will be 2 ½ times the age of her daughter . Calculate the sum of their present ages. (3marks)
1. Using a pair of compasses and a ruler only construct a triangle ABC and such that AB=4cm, BC=6cm and angle ABC=135°. (2marks)
2. Construct the height of triangle ABC in (a) above taking AB as the base, hence calculate the area of triangle ABC. (2marks)

SECTION II(50 MARKS) ATTEMPT FIVE QUESTIONS ONLY

1. In a safari rally drivers are to follow a route ABCD. B is 250km from A on a bearing of 075°, C is on a bearing of 110° from A and 280km from B. The bearing C from D is 220° and at a distance of 300km. By scale drawing, show the relative position of ABC and D. (5marks)
2. Determine
  1. the distance of A from C (1mark)
  2. the compass bearing of B from C. (2marks)
  3. The distance and the true bearing of A from D. (2marks)
The vertices of triangle PQR are P(2,4) Q(4,6) and R(5,1). The vertices of its image under a rotation are P¹(−3,−1) Q¹(−5,1) and R¹(0,2)
1. 1. On the grid provided, draw PQR and P¹Q¹R¹ (2marks)
  2. By construction, determine the centre and the angle of rotation. (3marks)
2. On the same grid as in a (i) above, draw.
  1. TriangleP¹¹Q¹¹R¹¹ the image of PQR under a reflection in the line y=0 and state its coordinates. (2mks)
  2. Triangle P¹¹¹Q¹¹¹R¹¹¹ is the image of P¹¹ Q¹¹ R¹¹ under an enlargement scale factor −1, centre(0,−4) and state its coordinates. (3marks)
A modern coast bus left Nairobi at 10.45 am and travelled towards Mombasa at an average speed of 60km/h. A Nissan matatu left Nairobi at 1.15pm on the same day and travelled towards Mombasa along the same road at an average speed of 100km/h. The distance between Nairobi and Mombasa is 500km.
1. Determine the time of the day when the Nissan matatu overtook the bus (5marks)
2. Both vehicles continued towards Mombasa at their original speeds. Find how long the matatu had to wait in Mombasa before the bus arrived. (5marks)
Jane bought 3 bags of sugar and 5 bags of rice for a total of sh29, 750. Had she bought 4 bags of sugar and 2 bags of rice she could have spent sh5250 less.
1. Form two equations that represent the information above. (2mks)
2. Calculate the cost of a bag of sugar and that of rice using the matrix method. (4marks)
3. Jane’s profit per bag of sugar was 18% while her profit per bag of rice was 30%
  1. Find the total amount that she received from her sales. (2marks)
  2. Calculate her percentage profit from the sale of all the sugar and rice. (2marks)
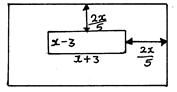
The following figure represents a dancing floor with a carpeted margin all around of ²/₅x wide leaving a dancing space of (x–3) cm by (x–3) cm.

If the total area of the entire room is 315m²
1. Calculate the value of x (5marks)
2. Calculate the area of the carpeted margin (3marks)
3. If the carpet cost sh750 per m², calculate the total cost of the sealed margin. (2marks)
A straight line L₁ has a gradient – ½ and passes through point P(−1, 3). Another line L2 passes through the points Q(1,−3) and R(4,5). Find:
1. The equation of L₁ (2marks)
2. The gradient of L₂ (1mark)
3. The equation of L₂ (2marks)
4. The equation of a line passing through a point S(0,5) and is perpendicular to L₂ (2marks)
5. The equation of a line through R parallel to L₁ (2marks)
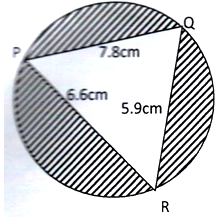
Triangle PQR is inscribed in the circle PQ=7.8cm, PR=6.6cm and QR=5.9cm.

Find
1. The radius of the circle, correct to one decimal place. (4marks)
2. The angles of the triangle (2marks)
3. The area of shaded region (4marks)
A particle travels in a straight line through a fixed point O. Its distance S metres from O is given by
S = 3t³ – 27t² + 72t + 4 where t is the time in seconds after passing O. Calculate
1. It distance after 3 seconds (2marks)
2. The value of t for which the particle is momentarily at rest. (3marks)
3. The velocity of the particle when t = 5 seconds. (2marks)
4. The maximum velocity of the particle. (3marks)

MARKING SCHEME

SECTION 1 (50 marks) Answer all questions in this section

Simplify without using a calculator. (3marks)
1⁴/₅ of ²⁵/₁₈ ÷ 1²/₃ × 24
2¹/₃ − ¼ of 12 ÷ ⁵/₃
Numerator
⁹/₅ × ²⁵/₁₈ = ⁵/₂
⁵/₂ × ³/₅ = ³/₂
³/₂ × 24 = 36 M1
Denominator
¼ × 12 = 3
3 × ³/₅ = ⁹/₅
⁷/₃ − ⁹/₅ = 35 − 27
15
= ⁸/₁₅ M1
^N/_D = 36 ÷ ⁸/₁₅
= 36 × ¹⁵/₈
= ¹³⁵/₂ = 67½ or 67.5 A1
Find the size of each interior angle of a regular pentagon. (3marks)
S = (n − 2)180
= (5 − 2)180
= 3 × 180 = 540
Each = ⁵⁴⁰/₅ M1
=108° A1
OR
³⁶⁰/₅ = 72
180 − 72
=108°
Find all the integral values of x which satisfy the inequalities. (3marks)
x + 8 > 4x – 6 ≥ 3(4 –x)
x + 8 > 4x – 6
–3x > –14
x < ¹⁴/₃
x < 4²/₃ M1
4x – 6 ≥ 12 – 3x
7x ≥ 18
x ≥ 2⁴/₇ M1

Integral values are 3, 4 A1
Three types of tea A, B and C are mixed in the ratio 2:3:5 by mass. Type A, B and C tea cost Ksh210, Ksh160 and Ksh120 respectively per kilogram. The blend is to be sold at a 30% profit. Determine the selling price of the blend per kilogram. (3marks)
Cost of the blend
²/₁₀ × 210 + ³/₁₀ × 160 + ⁵/₁₀ × 120
42 + 48 + 60 = 150 M1
S.P = ¹³⁰/₁₀₀ × 150 M1
= 195 A1
Determine the radius of a uniform cylindrical block 1.4m long and of density of 2.2g/cm³ if the mass is 47432g (π=²²/₇) (3marks)
Density = mass
volume
Volume = mass
density
= 47436 = 21560 ✓
2.2
V = πr²h
²²/₇ × r² × 140 = 21560
440r² = 21560  ✓
440 440
r² = 49
r = 7cm  ✓
A boy whose height is 1.5 stands on the horizontal ground and observes that the top of flag pole, 10m away, makes angle of elevation of 40°. Calculate the height of the flag post. (3marks)

Tan 40 = ^x/₁₀
x = 10 tan 40
= 8.39 ✓
H = 8.39 + 1.5 ✓
= 9.89 ✓
Two similar cylinders have total surface areas of 45cm² and 20cm². If the larger has a mass of 81g . Find the mass of the smaller one. (3marks)
A.S.F = ⁴⁵/₂₀ = ⁹/₄
L.S.F = √(⁹/₄) = ³/₂
V.S.F = (³/₂)³ = ²⁷/₈ ✓
⁸¹/_mass= ²⁷/₈
mass = 81 × 8 ✓
27
=24g ✓
Find the values of x and y in (4marks)
2^{3x +y} x 3^4x–y = 648

2^{3x +y} x 3^4x–y = 2³ × 3⁴ ✓
3x + y = 3
4x − y = 4
7x = 7
x = 1 ✓
but 3x + y = 3
3 + y = 3
y = 0 ✓
x = 1, y = 0 ✓
Simplify the following expression. (3marks)
3x² – 14xy – 5y²
3x² – 75y²
Numerator
3x² – 14xy – 5y²
P = –15 (–15 × 1)
S = –14 (–15 + 1)
3x² – 15xy + xy – 5y²
3x(x – 5y ) + y(x – 5y)
(x – 5y)(3x + y)  ✓
Denominator
3(x² – 25y²)
3(x + 5y)(x – 5y)  ✓
N = (x – 5y)(3x + y)
D   3(x + 5y)(x – 5y)
= 3x + y    ✓
3(x + 5y)
Use tables of reciprocals and cubes to evaluate to four significant figures. (3marks)
3 − 2
0.375³ 981.7
56.89 ✓ − 0.002037 ✓
= 56.89✓
On Saturday October 15, 2017 the following were the buying and selling prices of foreign currencies in a certain bank.

Buying(Ksh)   Selling(Ksh)

1 Euro   111.53 112.01

100 Japanese Yen 97.32 97.70

A Japanese travelling from Sweden arrived in Kenya with X Euros. He converted all the X Euros to Kenya shillings at the bank while in Kenya he spent a total of kenya shillings 350000 and then converted the remaining Kenya shillings to Japanese Yen at the same bank at the same rates. If the Japanese received 32669396 Yen. Calculate the value of X. (3marks)
X × 111.53
= 111.53X − 350000
(111.53X − 350000)× 100
97.70
=32669396
111.53X − 350000
= 31917999.892
111.53X =  32267999.892
111.53 111.53
X = 289321.25
The GCD is 1620, 1800 and a third number is 180. The LCM of the three numbers is 8100. Find the difference between greatest and smallest possible third number. (3marks)

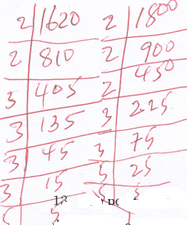
1620 = 2² × 3⁴  × 5
1800 = 2³  × 3²  × 5²
180 = 2²  × 3²  × 5
8100 = 2³  × 3⁴  × 5²X = 2²  × 3²  × 5²
= 16200 ✓
16200 − 180
= 16020 ✓
The position vectors of points A and B are and respectively, point C divides AB externally in the ratio 5:2. Find the position vector of C. (3marks)

C(−19, 8, −1) ✓
The average mark scored by the first 27 students in a mathematics test is 52. The average mark scored by the remaining 37 is 58. Calculate the mean mark for the whole class. (3marks)
Total = 27 × 52 + 37 × 58 ✓
64
= 3550
6
= 55.47 ✓
Five years ago, a mother’s age was four times that of the daughter. In four years to come, she will be 2 ½ times the age of her daughter . Calculate the sum of their present ages. (3marks)
Present ages
daughter = x
mother = y
Five years ago
Daughter = x − 5
mother = y − 5
y − 5 =4(x − 5)
y − 5 = 4x − 20
y = 4x − 15 ......(i)
Four years to come
x + 4
y + 4
(y + 4) = 2.5(x + 4)
y + 4 = 2.5x + 10
y = 2.5x + 6
4x − 15 = 2.5x + 6
1.5x = 21
x = 14
1. Using a pair of compasses and a ruler only construct a triangle ABC and such that AB=4cm, BC=6cm and angle ABC=135°. (2marks)
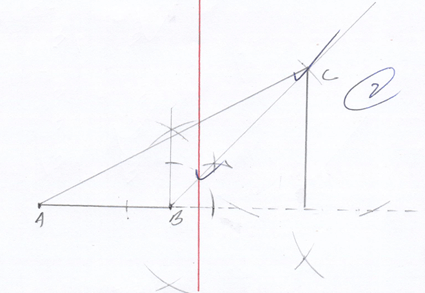
2. Construct the height of triangle ABC in (a) above taking AB as the base, hence calculate the area of triangle ABC. (2marks)
  h = 4.2 ✓
  Area = ½bh
  =½ × 4 × 4.2
  = 8.4cm² ✓

SECTION II(50 MARKS) ATTEMPT FIVE QUESTIONS ONLY

1. In a safari rally drivers are to follow a route ABCD. B is 250km from A on a bearing of 075°, C is on a bearing of 110° from A and 280km from B. The bearing C from D is 220° and at a distance of 300km. By scale drawing, show the relative position of ABC and D. (5marks)
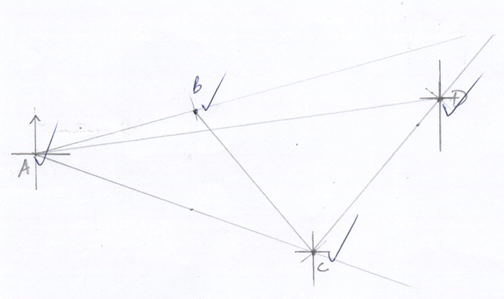
2. Determine
  1. the distance of A from C (1mark)
    9 × 50 = 450km ✓
  2. the compass bearing of B from C. (2marks)
    N39°W ✓
  3. The distance and the true bearing of A from D. (2marks)
    12.5 × 50 = 625km ✓
    bearing 264° ✓
The vertices of triangle PQR are P(2,4) Q(4,6) and R(5,1). The vertices of its image under a rotation are P¹(−3,−1) Q¹(−5,1) and R¹(0,2)
1. 1. On the grid provided, draw PQR and P¹Q¹R¹ (2marks)
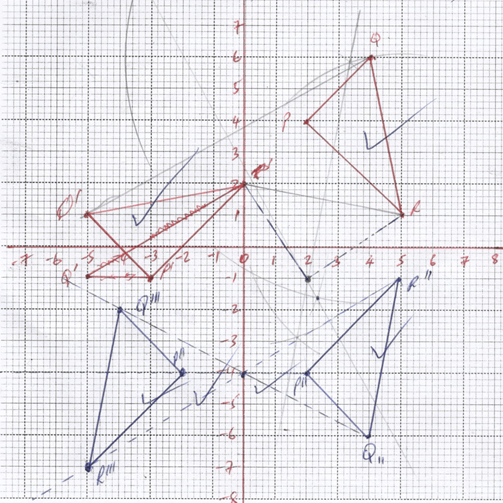
  2. By construction, determine the centre and the angle of rotation. (3marks)
    Centre (2, −1) +90°
2. On the same grid as in a (i) above, draw.
  1. TriangleP¹¹Q¹¹R¹¹ the image of PQR under a reflection in the line y=0 and state its coordinates. (2mks)
    P¹¹(2, −4), Q¹¹(4, −6) R¹¹(5, −1)
  2. Triangle P¹¹¹Q¹¹¹R¹¹¹ is the image of P¹¹ Q¹¹ R¹¹ under an enlargement scale factor −1, centre(0,−4) and state its coordinates. (3marks)
    P¹¹¹(−2, −4) Q¹¹¹(−4, −2) R¹¹¹(−5, −7)
A modern coast bus left Nairobi at 10.45 am and travelled towards Mombasa at an average speed of 60km/h. A Nissan matatu left Nairobi at 1.15pm on the same day and travelled towards Mombasa along the same road at an average speed of 100km/h. The distance between Nairobi and Mombasa is 500km.
1. Determine the time of the day when the Nissan matatu overtook the bus (5marks)
  
  Distance by bus
  box 2½ = 150km ✓
  Relative speed
  100 − 60 = 40km/h ✓
  Time = ¹⁵⁰/₄₀ = 3¾
  = 3hrs 45min ✓
  1:15 ✓
  +3:45
  5:00pm ✓
2. Both vehicles continued towards Mombasa at their original speeds. Find how long the matatu had to wait in Mombasa before the bus arrived. (5marks)
  60 × 3¾ = 225 ✓
  225
  +150
  375 ✓
  500
  −375
  125
  ¹²⁵/₆₀ = 2hrs 5min ✓
  ¹²⁵/₁₀₀ = 1hr 15min ✓
  2 05
  −1 15
  50
  = 50 min ✓
Jane bought 3 bags of sugar and 5 bags of rice for a total of sh29, 750. Had she bought 4 bags of sugar and 2 bags of rice she could have spent sh5250 less.
1. Form two equations that represent the information above. (2mks)
  Let the price of sugar = x
  let the price of rice = y
  3x + 5y = 29750
  4x + 2y = 24500
2. Calculate the cost of a bag of sugar and that of rice using the matrix method. (4marks)
  
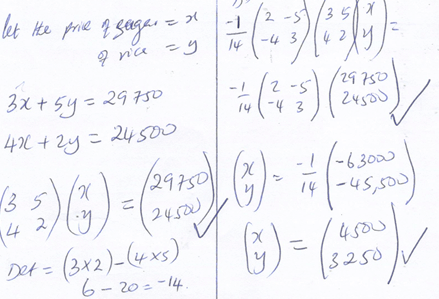
  a bag of sugar cost Sh. 4500 ✓
  a bag of rice cost Sh. 3250
3. Jane’s profit per bag of sugar was 18% while her profit per bag of rice was 30%
  1. Find the total amount that she received from her sales. (2marks)
    3 × ¹¹⁸/₁₀₀ × 4500 ✓ + 5 × ¹³⁰/₁₀₀ × 3250 ✓
    = 37,055 ✓
  2. Calculate her percentage profit from the sale of all the sugar and rice. (2marks)
    Profit = Sales − cost
    = 37055 − 29750
    = 7,305  ✓
    7305  × 100  ✓
    29750
    = 24.55%  ✓
The following figure represents a dancing floor with a carpeted margin all around of ²/₅x wide leaving a dancing space of (x–3) cm by (x–3) cm.

If the total area of the entire room is 315m²
1. Calculate the value of x (5marks)
  L = x + 3 + 4x = 5x + 15 + 4x
  1 5 5
  = 9x + 15   ✓
  5
  W = x − 3 + 4x = 5x − 15 + 4x
  1 5 5
  = 9x − 15   ✓
  5
  = (9x + 15)   × (9x − 15) = 315
  5 5
  81x² − 225 = 315   ✓
  25
  81x² − 225 = 7875   ✓
  81x² = 8100
  x² = 100
  x = 10   ✓
2. Calculate the area of the carpeted margin (3marks)
  Area of smaller
  7 × 13 = 91 ✓
  315 − 91 ✓ = 224m² ✓
3. If the carpet cost sh750 per m², calculate the total cost of the sealed margin. (2marks)
  750 × 224 ✓
  = 168,000 ✓
A straight line L₁ has a gradient – ½ and passes through point P(−1, 3). Another line L2 passes through the points Q(1,−3) and R(4,5). Find:
1. The equation of L₁ (2marks)
  y − 3 = ⁻½
  x + 1
  2y − 6 = − x −1
  2y = −x + 5
  2y + x = 5
2. The gradient of L₂ (1mark)
  gradient = Δy = 5−−3
  Δx 4−1
  = ⁸/₃
3. The equation of L₂ (2marks)
  y + 3 = ⁸/₃
  x − 1
  3y + 9 = 8x − 8
  3y = 8x − 17
4. The equation of a line passing through a point S(0,5) and is perpendicular to L₂ (2marks)
  M₁ = ⁸/₃
  M₂ = ⁻³/₈
  y − 5 = ⁻³/₈
  x
  8y − 40 = − 3x
  8y + 3x = 40
5. The equation of a line through R parallel to L₁ (2marks)
  M₁ = ⁻¹/₂
  M₂ =⁻¹/₂
  y − 5 = ⁻¹/₂
  x − 4
  2y − 10 = −x + 4
  2y = −x + 14
  2y + x = 14
Triangle PQR is inscribed in the circle PQ=7.8cm, PR=6.6cm and QR=5.9cm.

Find
1. The radius of the circle, correct to one decimal place. (4marks)
  r = abc
  4A
  s = 7.8 + 6.6 + 5.9
  2
  =10.15
  A = √(10.15(2.35)(3.55)(4.25))
  A = 18.97036093
  r = 7.8 × 6.6 × 5.9
  4 × 18.97036093
  = 4.00cm
2. The angles of the triangle (2marks)
  Q = 2r
  Sin A
  6.6 = 2×4
  Sin Q
  8 sin Q = 6.6
  Sin Q = ^6.6/₈ = 0.825
  Q = 55.59°
  5.9 = 2×4
  Sin P
  8 Sin P = 5.9
  Sin P = ^5.9/₈ = 0.7375
  P = 47.52°
  7.8 = 2×4
  Sin R
  8 Sin R = 7.8
  Sin R ^7.8/₈ = 0.975
  R = 77.16°
3. The area of shaded region (4marks)
  Area of circle =πr²
  = ²²/₇ × 4 × 4
  = 50.2857
  50.2857
  −18.9704
  31.2953
A particle travels in a straight line through a fixed point O. Its distance S metres from O is given by
S = 3t³ – 27t² + 72t + 4 where t is the time in seconds after passing O. Calculate
1. It distance after 3 seconds (2marks)
  at t = 3
  S = 3(3)³ – 27(3)² + 72(3) + 4 ✓
  = 81 − 243 + 216 + 4
  = 58m ✓
2. The value of t for which the particle is momentarily at rest. (3marks)
  at rest v = 0
  V = ^ds/_dt = 9t² − 54t + 72 = 0
  9t² − 54t + 72 = 0
  t² − 6t + 8 = 0
  P = 8 (−2 × −4)
  s = −6 (−2−4)
  t²− 2t − 4t + 8 = 0
  t(t − 2) −4 (t − 2)
  (t − 2)(t − 4) = 0
  t = 2 or t = 4
3. The velocity of the particle when t = 5 seconds. (2marks)
  V = 9t² − 54t + 72
  at t = 5
  V = 9(5)² − 54(5) + 72
  225 − 270 +72
  = 27m/s
4. The maximum velocity of the particle. (3marks)
  at max V a = 0
  a = ^dv/_dt = 18t  − 54
  18t  − 54 = 0
  18t = 54
  t = 3
  Velocity at t = 3
  9(3)²  − 54(3) + 72
  = 81  − 162 + 72
  =  − 9m/s