Instructions to candidates
- Write your name and admission number in the spaces provided above.
- This paper consists of two sections: Section I and Section II.
- Answer all the questions in Section I and only five questions from Section II.
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

QUESTIONS
SECTION 1 (50 marks) Answer all questions in this section
- Use logarithms to evaluate , (4marks)
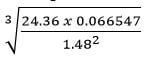
- Make d the subject of the formula (3marks)
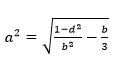
- Simplify the following surds leaving your answer in the form a+ b√c (3marks)
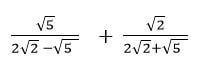
-
- Expand the binomial expression
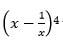 up to the third term. (1mark)
up to the third term. (1mark) - Use the expansion above (where x > 1) to estimate the value of (99)4 to 3 s.f. (2marks)
- Expand the binomial expression
- A(3,2) and B(7,4) are points on the circumference of a circle. Given that chord AB passes through the centre of the circle determine the equation of the circle. (4marks)
- Without using logarithms tables of calculator: Evaluate. (3marks)
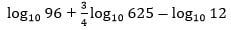
- Solve for x given that the following is a singular matrix. (3mks)
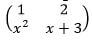
- The sides of a triangle were measured and recorded as 8.4 cm, 10.5 cm and 15.32 cm . Calculate the percentage error in it’s perimeter 2d.p. (3marks)
- Given that 64, b, 4…. are in continued proportion, find the value of b. (3marks)
- The figure below shows a circle centre O. AB and PQ are chords intersecting externally at a point C. AB=9cm, PQ=5cm and Qc =4cm, find the length BC.(3marks)
- Two variables x and y are such that y varies directly as xn where n is a constant. Given that y=320 when x=16 and y = 2560 when x = 64. Find the value of n. (3marks)
- A man sold a motor cycle at 84000. The rate of depreciation was 5% per annum. Calculate the value of the motor cycle after 3 years to 1d.p. (3marks)
- Vector r has a magnitude of 14 and is parallel to vector s. Given that s = 6i – 2j +3k, express vector r in terms of i, j and k. (3marks)
- Solve for x in the range 0 ≤ x ≤ 360º
If 2sin2x + sin x – 1=0 (4marks) - The prefects body of a certain school consists of 7 boys and 5 girls. Three prefects are to be chosen at random to represent the school at a certain function at Nairobi. Find the probability that the chosen prefects are boys. (2mks)
- A trigonometric function is given as (4mks)
y = 0.5 cos (2x – 40)º
Determine- Amplitude
- Period
- Phase angle
SECTION B(50 MARKS)
Answer any five questions from this section in the spaces provided.
-
-
- Taking the radius of the earth, R=6370km and π=22/7, calculate the shortest distance between two cities P(600N, 290W) and Q(600N, 310E) along the parallel of latitude. (3marks)
- If it is 1200hrs at P, what is the local time at Q (3marks)
- An aeroplane flew due south from a point A(60ºN, 45ºE) to a point B, the distance covered by the aeroplane was 8000km, determine the position of B. (4marks)
-
- The diagram below shows a square based pyramid V vertically above the middle of the base. PQ=10cm and VR=13cm. M is the midpoint of VR.
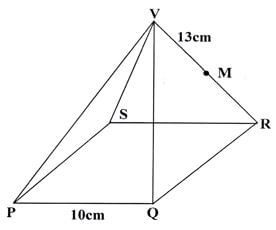
Find-
- the length PR. (2marks)
- the height of the pyramid (2marks)
-
- the angle between VR and the base PQRS (2marks)
- the angle between MR and the base PQRS (2marks)
- the angle between the planes QVR and PQRS. (2marks)
-
- Complete the following table for the equation
- y = 2x3 + 3x2 –6x –4 for the values –3≤ x ≤ 2 (2marks)
x
-3
-2
-1
0
1
2
2x3
-16
0
2
16
3x2
27
3
0
12
-6x
12
0
-12
-4
-4
-4
-4
-4
-4
-4
y
4
-4
12
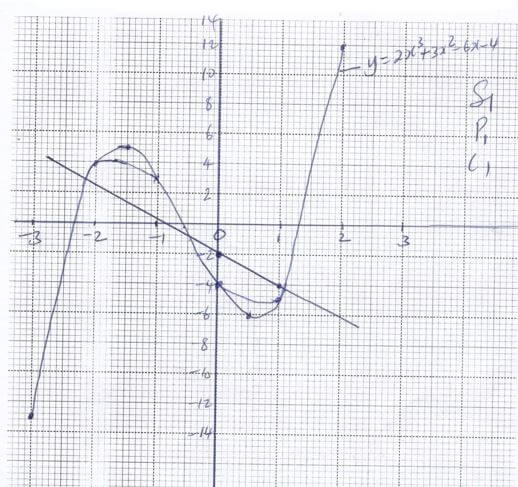
- On the grid provided draw the graph of y=2x3 + 3x2 – 6x – 4 (3marks)

- By drawing a suitable straight lines use your graph to solve the equations
- 2x3 + 3x2 – 4x – 2 =0 (2marks)
- 2x3 + 3x2 – 6x – 4 =0 (3marks)
- y = 2x3 + 3x2 –6x –4 for the values –3≤ x ≤ 2 (2marks)
- The diagram below shows a triangle OPQ in which M and N are points on OQ and PQ respectively such that OM= 2/3 OQ and PN = 1/4PQ. Lines PM and ON meets at X.
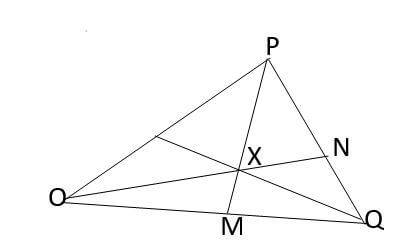
- Given that OP = p and OQ= q express in term of p and q the vectors.
- PQ (1mark)
- PM (1marks)
- ON (1marks)
- You are further given that OX=KON and PX=hPM.
- Express OX in terms of P and q in two different ways. (2marks)
- Find the value of h and K. (4marks)
- Find the ratio PX:XM (1mark)
- Given that OP = p and OQ= q express in term of p and q the vectors.
- In the figure below , O is the centre of the circle.PQR is a tangent to the circle at Q. Angle PQS=28º, angle UTQ=54º and UT=TQ
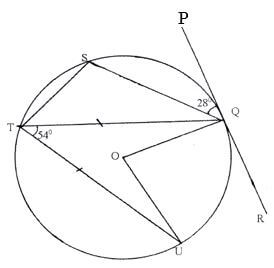
Giving reasons, determine the size of- Angle STQ (2mks)
- Angle TQU (2mks)
- Angle TQS (2mks)
- Reflex angle UOQ (2mks)
- Mr. Kimutai a teacher from Tuiyotich Secondary School earns K£12000 per annum and lives in a house provided by the employer at a minimum rent of Ksh2000 per month. He gets a family relief of K£1320p.a and is entitled to a relief of 10% of his insurance of K£800p.a.
- Calculate his annual tax bill based on the table below. (6mks)
Income slab in k£p.aRate
1 – 2100 10%
2101 – 4200 15%
4201 – 6300 25%
6301 – 8400 35%
Over 8400 45% - Kimutai other deductions include.
- W.C.P.S = sh600.00pm
- NHIF = sh500.00pm
Calculate Kimutai’s net salary monthly. (4mks)
- Calculate his annual tax bill based on the table below. (6mks)
-
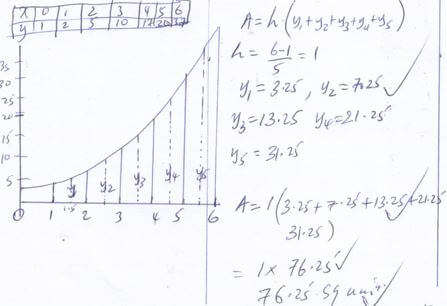
- Use the mid-ordinate rule with five strips to estimate the area bounded by the curve y = x2 +1, the x–axis, lines x=1 and x=6 (4mks)
- Find the exact area of the region in (a) above (3mks)
- Calculate the percentage error in area when mid-ordinate rule is used. (3mks)
- An arithmetic progression AP has the first term a and the common difference d.
- Write down the third, ninth and twenty fifth terms of the AP in terms of a and d. (2mks)
- The AP above is increasing and the third, ninth and twenty fifth terms form the first three consecutive terms of a geometric progression (G.P). The sum of the seventh and twice the sixth term of AP is 78. Calculate
- The first term and common difference of the A.P (5mks)
- The sum of the first 5 terms of the G.P (3mks)

MARKING SCHEME
SECTION 1 (50 marks) Answer all questions in this section
- Use logarithms to evaluate , (4marks)
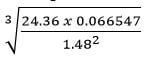
No Log 24.36 1.3867 0.066547 2.8231 0.2098 1.482 0.1703 x 2 0.3406 1.8692
39.045 x 10-1 1.9564 0.9045 - Make d the subject of the formula (3marks)
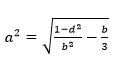
a4 = 1 -d2 - b
b2 3
1 - d2 = a4 + b/3
b2
1 - d2 = a4b2 + b3
3
d2 = 1 - a4b2 + b
3
d = ±√1 - a4b2 + b
3 - Simplify the following surds leaving your answer in the form a+ b√c (3marks)
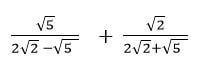
√5(2√5 + √5) + √2(2√2 - √5)
(2√2)2 - (√5)2
=2√10 + 5 + 4 - √10
8 - 5
= 9 + √10
3 -
- Expand the binomial expression
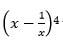 up to the third term. (1mark)
up to the third term. (1mark)
x4 - 4x2 + 6 + ....................... - Use the expansion above (where x > 1) to estimate the value of (99)4 to 3 s.f. (2marks)
(9.9)4 = (10 - 1/10)4
(x - 1/x)4 = (10 - 1/10)4
x = 10
(9.9)4 = (10)4 - 4(10)2 + 6
=10000 - 400 + 6
=9606
- Expand the binomial expression
- A(3,2) and B(7,4) are points on the circumference of a circle. Given that chord AB passes through the centre of the circle determine the equation of the circle. (4marks)
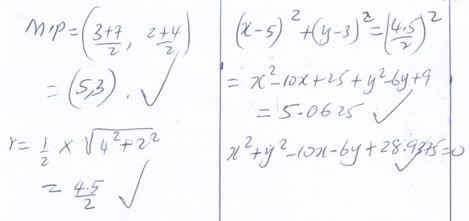
- Without using logarithms tables of calculator: Evaluate. (3marks)
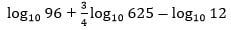
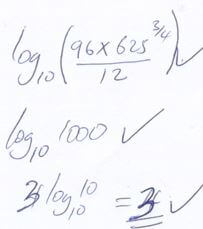
- Solve for x given that the following is a singular matrix. (3mks)
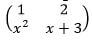
(x + 3) - 2x2 = 0
2x2 - x - 3 = 0
p = -6
2x - 3
-1
2 - 3
2x2 + 2x - 3x - 3 = 0
2x(x + 1) - 3(x + 1) = 0
(x - 1) (2x - 3) = 0
x + 1 = 0or 2x - 3 = 0
x = -1 2x = 3
x = 3/2
x = -1 or 1.5 - The sides of a triangle were measured and recorded as 8.4 cm, 10.5 cm and 15.32 cm . Calculate the percentage error in it’s perimeter 2d.p. (3marks)
max per = 8.45 + 10.55
+15.325
=34.325
min per = 8.35 + 10.45 + 15.315
=34.115
absolute error = 34.325 - 34.115
2
= 0.21 = 0.105
2
actual 8.4 + 10.5 + 15.32
=34.22
% error = 0.105 x 100
34.22
= 0.3068% - Given that 64, b, 4…. are in continued proportion, find the value of b. (3marks)
64 = b
b 4
b2 = 256
b = 16 - The figure below shows a circle centre O. AB and PQ are chords intersecting externally at a point C. AB=9cm, PQ=5cm and Qc =4cm, find the length BC.(3marks)

x(x + 9) = 4 x 9
x2 + 9x - 36 = 0
BC = 3 cm - Two variables x and y are such that y varies directly as xn where n is a constant. Given that y=320 when x=16 and y = 2560 when x = 64. Find the value of n. (3marks)
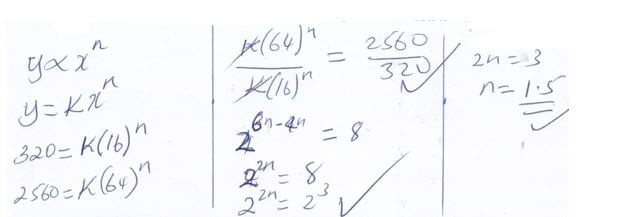
- A man sold a motor cycle at 84000. The rate of depreciation was 5% per annum. Calculate the value of the motor cycle after 3 years to 1d.p. (3marks)
A = p - (1 - r/100)n
A = ??
p = 84 000
n = 3
r = 5%
A = 84000(1 - 5/100)3
= 84000(0.95)3
5% = 72019.5 - Vector r has a magnitude of 14 and is parallel to vector s. Given that s = 6i – 2j +3k, express vector r in terms of i, j and k. (3marks)

- Solve for x in the range 0 ≤ x ≤ 360º
If 2sin2x + sin x – 1=0 (4marks)
- The prefects body of a certain school consists of 7 boys and 5 girls. Three prefects are to be chosen at random to represent the school at a certain function at Nairobi. Find the probability that the chosen prefects are boys. (2mks)
p = 7/12 x 6/11 x 5/10
= 7/22 - A trigonometric function is given as (4mks)
y = 0.5 cos (2x – 40)º
Determine- Amplitude
0.5 - Period
360 = 180
2 - Phase angle
40º
- Amplitude
SECTION B(50 MARKS)
Answer any five questions from this section in the spaces provided.
-
-
- Taking the radius of the earth, R=6370km and π=22/7, calculate the shortest distance between two cities P(600N, 290W) and Q(600N, 310E) along the parallel of latitude. (3marks)
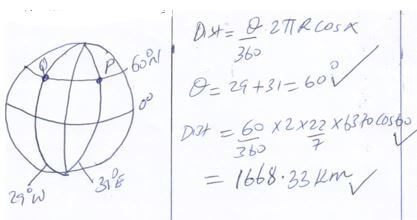
- If it is 1200hrs at P, what is the local time at Q (3marks)
θ = 60
time diff = 4θ
=4 x 60 = 240
= 4hrs
1200
4
= 0800 hrs
- Taking the radius of the earth, R=6370km and π=22/7, calculate the shortest distance between two cities P(600N, 290W) and Q(600N, 310E) along the parallel of latitude. (3marks)
- An aeroplane flew due south from a point A(60ºN, 45ºE) to a point B, the distance covered by the aeroplane was 8000km, determine the position of B. (4marks)
dist = θ 2πR
360
θ x 2 x 22 x 6370 = 8000
360 7
1001θ = 8000
9
θ = 71.92º
71.92º - 60
=11.92º
B(11.92ºS, 45ºE)
-
- The diagram below shows a square based pyramid V vertically above the middle of the base. PQ=10cm and VR=13cm. M is the midpoint of VR.

Find-
- the length PR. (2marks)
PR = √102 + 102
=√200
=14.14 cm - the height of the pyramid (2marks)
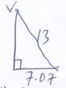
h = √132 + 7.072
=√161.93
=12.73cm
- the length PR. (2marks)
-
- the angle between VR and the base PQRS (2marks)
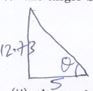
Tan θ = 12.73
5
= 2.546
θ = Tan -12.546
=68.56º - the angle between MR and the base PQRS (2marks)
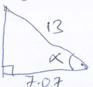
cos α = 7.07
13
= 0.5438
α = 57.06º - the angle between the planes QVR and PQRS. (2marks)
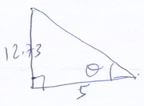
Tan θ = 12.73
5
=2.546
θ = Tan -12.546
=57.06º
- the angle between VR and the base PQRS (2marks)
-
- Complete the following table for the equation
- y = 2x3 + 3x2 –6x –4 for the values –3≤ x ≤ 2 (2marks)
x
-3
-2
-1
0
1
2
2x3
-54 -16
-2 0
2
16
3x2
27
3
0
12
-6x
18 12
6 0
-12
-4
-4
-4
-4
-4
-4
-4
y
-13 4
3 -4
-5 12
- On the grid provided draw the graph of y=2x3 + 3x2 – 6x – 4 (3marks)
- By drawing a suitable straight lines use your graph to solve the equations
- 2x3 + 3x2 – 4x – 2 =0 (2marks)
x = -2.2 or - 0.5 or 1.1 - 2x3 + 3x2 – 6x – 4 =0 (3marks)
y = 2x3 + 3x2 – 6x – 4
0 = 2x3 + 3x2 – 6x – 4
y = 0
x = -2.35 or 1.3 0r - 0.6
- 2x3 + 3x2 – 4x – 2 =0 (2marks)
- y = 2x3 + 3x2 –6x –4 for the values –3≤ x ≤ 2 (2marks)
- The diagram below shows a triangle OPQ in which M and N are points on OQ and PQ respectively such that OM= 2/3 OQ and PN = 1/4PQ. Lines PM and ON meets at X.

- Given that OP = p and OQ= q express in term of p and q the vectors.
- PQ (1mark)
= q - p - PM (1marks)
2/3q - p - ON (1marks)
= 3/4p + 1/4q
- PQ (1mark)
- You are further given that OX=KON and PX=hPM.
- Express OX in terms of P and q in two different ways. (2marks)
ox = (1 - h)p + 2/3hq - Find the value of h and K. (4marks)
k = 8/9 - Find the ratio PX:XM (1mark)
=1:2
- Express OX in terms of P and q in two different ways. (2marks)
- Given that OP = p and OQ= q express in term of p and q the vectors.
- In the figure below , O is the centre of the circle.PQR is a tangent to the circle at Q. Angle PQS=28º, angle UTQ=54º and UT=TQ

Giving reasons, determine the size of- Angle STQ (2mks)
28º angles in alternate segment are equal - Angle TQU (2mks)
63º base angles of isosceless triangle are equal - Angle TQS (2mks)
35º angles on a staright line add up to 180º - Reflex angle UOQ (2mks)
252º angles at a point add up to 360º
- Angle STQ (2mks)
- Mr. Kimutai a teacher from Tuiyotich Secondary School earns K£12000 per annum and lives in a house provided by the employer at a minimum rent of Ksh2000 per month. He gets a family relief of K£1320p.a and is entitled to a relief of 10% of his insurance of K£800p.a.
- Calculate his annual tax bill based on the table below. (6mks)
Income slab in k£p.aRate
1 – 2100 10%
2101 – 4200 15%
4201 – 6300 25%
6301 – 8400 35%
Over 8400 45%
- Kimutai other deductions include.
- W.C.P.S = sh600.00pm
- NHIF = sh500.00pm
Calculate Kimutai’s net salary monthly. (4mks)
gross income
12000 x 20 = 20000
12
total deductions
3791.67 + 600 + 500 = 4891.67
net income
= 20 000 - 4891.67
= 15108.33
- Calculate his annual tax bill based on the table below. (6mks)
-
- Use the mid-ordinate rule with five strips to estimate the area bounded by the curve y = x2 +1, the x–axis, lines x=1 and x=6 (4mks)
- Find the exact area of the region in (a) above (3mks)
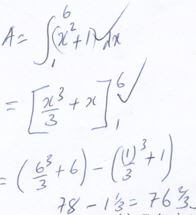
= 762/3 - Calculate the percentage error in area when mid-ordinate rule is used. (3mks)
error =762/3 - 76.25
= 0.417
0.417 x 100
762/3
= 0.543
- Use the mid-ordinate rule with five strips to estimate the area bounded by the curve y = x2 +1, the x–axis, lines x=1 and x=6 (4mks)
- An arithmetic progression AP has the first term a and the common difference d.
- Write down the third, ninth and twenty fifth terms of the AP in terms of a and d. (2mks)
T3 = a + 2d
Ta = a + 8d
T25 = a + 24d - The AP above is increasing and the third, ninth and twenty fifth terms form the first three consecutive terms of a geometric progression (G.P). The sum of the seventh and twice the sixth term of AP is 78. Calculate
- The first term and common difference of the A.P (5mks)

- The sum of the first 5 terms of the G.P (3mks)

- The first term and common difference of the A.P (5mks)
- Write down the third, ninth and twenty fifth terms of the AP in terms of a and d. (2mks)
Download Mathematics Paper 2 Questions and Answers - Nyeri Mocks 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

