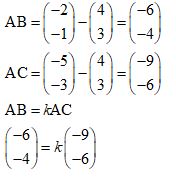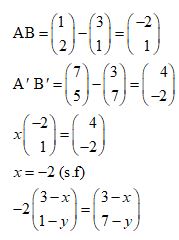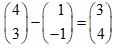Questions
Instructions to candidates
- The paper contains TWO Sections: Section I and Section II.
- Answer ALL the questions in Section I and Only five questions from Section II.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Answer all the questions in English.
SECTION I (50 marks)
Answer all questions in this section in the spaces provided
- All odd numbers from are arranged in descending order to form a number.
-
- Write the number (1 mark)
- Write the total value of the second digit of the number formed in (a) (i) (1 mark)
- Express the value of the number in (a) (ii) as a product of its prime factors in power form.(2 marks)
-
- A shopkeeper bought a bag of sugar. He intends to repack the sugar in 40g,250g and 750g . Determine the least mass in grams of sugar that was in the bag. (3 marks)
- Given that Log102= 0.3010 and Log102= 0.4771 without using tables or calculator find correct to 4 significant figures. (3 marks)
- Evaluate (3 marks)
½ of ³/₂+1½(2½ - ²/₃)
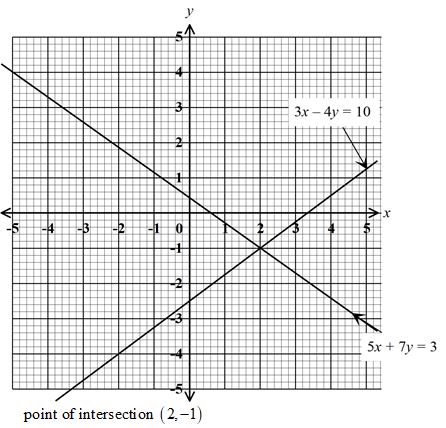
¾ of 2½ ÷½ - Using the grid provided below, solve the simultaneous equation (3 marks)
- Given that a chord of length subtends an angle of at the circumference of the circle. Calculate the radius of the circle. (3 marks)
- When a shopkeeper sells articles at , he makes a profit on the cost price. During a sale, he reduced the price of each article to . Calculate the percentage profit on an article sold at the sale price. (3 marks)
- The size of one interior angle of an irregular polygon is 80°. Each of the other interior angles is 128°. Find the number of sides of the polygon. (3 marks)
- Simplify 81¾ - (1/5)-1 - 270(2 marks)
- Given the inequalities x-6 < -3x + 2 < -2x + 9
- Solve the inequality (3 marks)
- Represent on a number line (1 mark)
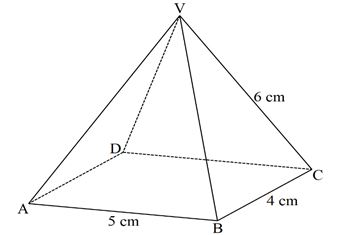
- The diagram below represents a right rectangular based pyramid of 5 cm by 4 cm. The slant edge of the pyramid is 6 cm. Draw and label the net of the pyramid. (3 marks)
- Vectors OA = 4i + 3j,OB= -2i -j and OC=-5i-3j . Show that points A, B and C are collinear.(3 marks)
- Find the period , amplitude and phase angle of the function 2y=3sin (½x - 60°)(3 marks)
- Simplify (3 marks)
20 - 11x - 3x2
16x - 12x2 - Write the following ratios in ascending order 2:3,15:16 ,7:6 13:15, (3 marks)
- Under an enlargement, the image of the points A(3,1) and B(1,2) are A'(3,7) and B'(7,5) . Find the centre and scale factor of enlargement. (4 marks)
SECTION II (50 marks)
Answer only five questions in this section in spaces provided
- A straight line passes through P(-1,1) and Q(3,4) .
- Find the length of line PQ(2 marks)
- Find the equation of the perpendicular bisector of line PQ , leaving the equation in the form y=mx+c(4 marks)
- Determine the equation of line parallel to line and passes through point (2,3), leaving your answer in double intercept form. Hence state the y intercept. (4 marks)
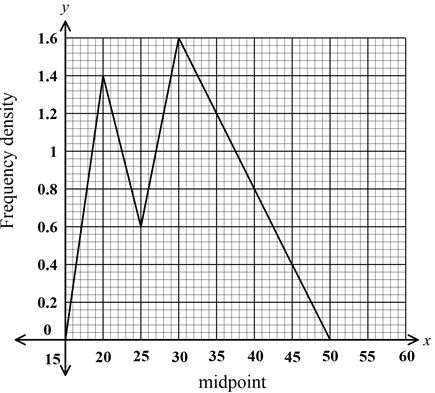
- The marks scored by 30 students in test were recorded as follows
41 43 34 28 19 22
32 38 22 18 25 33
30 41 36 31 28 37
35 34 19 22 29 23
29 44 26 27 29 36- Starting with the class 18-22 , make a frequency distribution table for the data. (2 marks)
- Using the frequency distribution in (a) above calculate :
- the mean (2 marks)
- the median (3 marks)
- Draw a frequency polygon to represent the data. (3 marks)
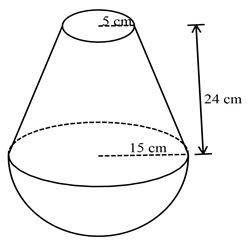
- The solid below is made up of hemispherical part and a frustum of cone. The top and bottom radius of the frustum are and respectively. The vertical height of the frustum is .
- Determine the vertical height of the cone from which the frustum was cut. (2 marks)
- Calculate
- The volume of the solid correct to 2 decimal places (3 marks)
- The surface area of the solid correct to 2 decimal places (5 marks)
-
-
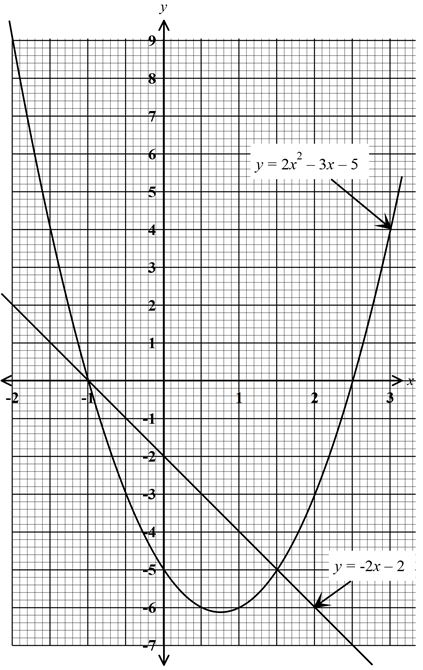
- Draw the graph of the function for y= 2x2 - 3x - 5 for -2< x < 3(5 marks)
- Use the graph to solve the equation 2x2 - 3x - 5=0(1 mark)
- Use the graph to solve the simultaneous equation y=2x2 - 3x - 5 and y=-2x-2 (3 marks)
- Write down the quadratic equation which the line y=-2x-2 is solving. (1 marks)
-
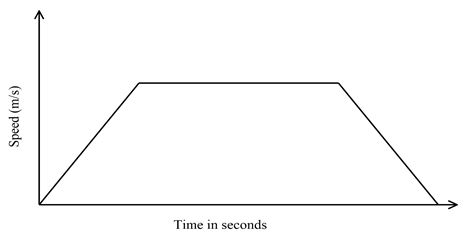
- The diagram below shows the speed time graph for a bus travelling between two stations, the bus starts from rest and accelerates uniformly for 75 seconds. It then travels at constant speed for 150 seconds and finally decelerates uniformly for 100 seconds.
- Given that the distance between the two stations is . Calculate
- maximum speed in attained by the bus. (3 marks)
- the acceleration of the bus (2 marks)
- A van left Nairobi at 8.30 a.m and travelled towards Mombasa at an average speed of At 8.30 am a car left Nairobi and travelled along the same road at an average speed of .
- Calculate the distance covered by the car to catch up with the van. (4 marks)
- Find the time of the day when the car caught up with van. (1 mark)
- Given that the distance between the two stations is . Calculate
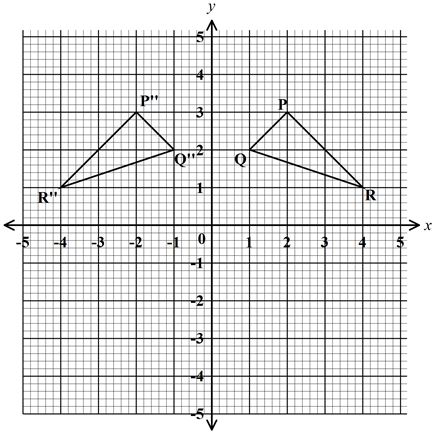
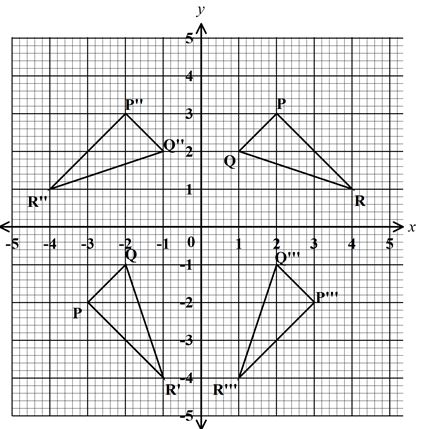
- On the Cartesian plane below, triangle PQR has vertices P(2, 3), Q(1, 2) and R(4, 1) while triangle P’’Q’’R’’ has vertices P’’(-2, 3), Q’’(-1, 2) and R’’(-4, 1).
- Describe fully the transformation which maps triangle PQR onto triangle P’’Q’’R’’.(1 mark)
- On the same plane, draw triangle P’Q’R’, the image of triangle PQR under a reflection in the line (2 marks)
- Describe fully a single transformation which maps triangle P’Q’R’ onto triangle P’’Q’’R’’ (2 marks)
- Draw triangle P’’’Q’’’R’’’ such that it can be mapped onto triangle PQR by a positive quarter turn about (0, 0) (3 marks)
- State a pair of triangles that is
- oppositely congruent (1 mark)
- directly congruent (1 mark)
- The equation of the curve is y=x3 - 2x2 -1
- Determine
- the stationary points (4 marks)
- the nature of the stationary points in (a) (i) above (2 marks)
- Determine
- the equation of the tangent to the curve at x=1 (2 marks)
- the equation of the normal to the curve at x=1 (2 marks)
- Determine
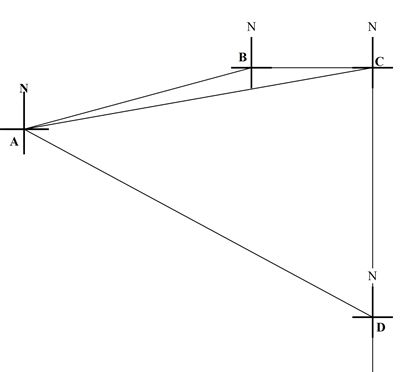
- The boundaries of ranch AB, BC , CD and DA are straight lines such that B is 075° from A and a distance of 50km. C is due east of B and a bearing of N80°E from A. D is due south of C and a distance of 70km.
- Using a scale of 1 cm to represent 10 km. show the relative positions of ABCD.(3 marks)
- From the scale drawing, determine
- the distance in kilometres between and (2 marks)
- the bearing of from (2 marks)
- the shortest distance from to border (1 mark)
- Calculate the area of the ranch in square kilometer. (2 marks)
Marking Scheme
-
- 97531
- 7000
- 23 x 53 x 7
- 40= 23 x 5
250= 2 x 53
750 = 2 x 3 x 53
LCM= 23 x 3 x 53
= 3000 - =log(2²x 3²)
103
2log2 + 2log 3 - 3log10
2(0.3010) + 2(0.4771) - 3
= -1.4438
= -1.444 - Num 3/4 x 11/2 x 11/6 = 3/4 + 11/4 = 14/4
Den 3/4 x 5/2 ÷ 1/2 = 15/4
= 14/4 x 4/15 = 14/15 -
- Angle at the centre = 1.2° x 2 = 2.4°
2.4 x 180/π = 137.51°
137.51° ÷ 2 = 68.75°
sin 68.75°= 5/r
r= 5.365cm - Cost price = 100/130 x 24.05 = 18.5
=22.95 - 18.5 = 4.45
= 4.45 x 100%
18.5
= 24.05% - 80 + 128(n-1)= (n-2)180
80 + 128n - 128 = 180n - 360
-48 + 360 = 180n - 128n
312= 52n
n=6 - = (34)¾ - 5 - 1
=27 - 5 - 1 =21 -
- x - 6 < -3x + 2
4x < 8
x< 2
-3x + 2 < -2x + 9
-7 < x
-7 < x < 2 -
- x - 6 < -3x + 2
-
-
AB = 2/3AC
AB/AC
A, shared point
hence point A, B and C are colinear - Amplitude = 1.5
period 360 ÷ 0.5 = 720°
phase angle - 60° - Num
3x2 + 11x - 20
3x2 + 15x - 4x - 20
3x(x+5)- 4(x + 5)
(3x - 4)(x + 5)
Den 4x(4-3x)
= (3x-4)(x+5)
4x(4-3x)
= -x-5
4x - 2 x 80 = 160
3 x 80 240
15 x 15 = 225
16 x 15 240
7 x 40 = 280
6 x 40 240
13 x 16 = 208
15 x 16 240
7:6, 15:16 , 13:15, 2:3 -
-2(3 - x)= 3 - x
-6 + 2x= 3 - x
3x = 9
x=3
-2(1-y)= 7 -y
-2 + 2y = 7-y
3y=9
y=3
(3,3) -
-
= √(32 + 42)
= 5 - Mid point
(-1 + 3 , 1 + 4)= (1, 2.5)
2 2
Gradient of PQ
= 4-1 = 3/4
3 + 1
m2 = -4/3
y - 2.5 = -4/3
x -1
3(y-2.5)= -4(x -1)
3y = -4x + 11.5
y = -4/3x + 35/6 - y - 3 = 3/4
x -2
4y - 12 = 3x -6
4y/6 - 3x/6 = 6/6
-x/2 + y/1.5 = 1
y intercept = 1.5
-
-
-
Marks Frequency midpoint(x) fx cf 18 - 22
23 - 27
28 - 32
33 - 37
38 - 42
43 - 477
3
8
6
4
220
25
30
35
40
45140
75
240
210
160
907
10
18
24
28
30 -
- Σfx = 915
Σf 30
= 30.5 - = 28.5 + (15 - 10/8)5
= 31.625
- Σfx = 915
-
-
-
- x = 5/15
x+24
15x = 5x + 120
10x = 120
x =12cm -
- volume = (1/3 x 22/7 x 152 x 36 - 1/3 x 22/7 x 52 x 12) + 2/3 x 22/7 x 153
(8,845.71 - 314.29) + 7071.43
= 15242.86 - √(122 + 52) = 13
√(362 + 152) = 39
S.A = (22/7 x 15 x 39 - 22/7 x 5 x13)+ 2 x 22/7 x 152 + 22/7 x 52
= 3048.57cm2
- volume = (1/3 x 22/7 x 152 x 36 - 1/3 x 22/7 x 52 x 12) + 2/3 x 22/7 x 153
- x = 5/15
-
-
-
- x = -1 and x = 2.5
-
- x = -1, y=0
x = 1.5, y=-5 - 2x2 - 3x - 5 = -2x -2
2x2 - x -3 = 0
-
-
-
- 1/2(150 + 325)h = 5225
h= 22 m/s - 22 - 0 = 0.2933 m/s
75
- 1/2(150 + 325)h = 5225
-
- time difference 8:30 am - 8:00am = 0.5hr
Distance covered by van 0.5 x 80 = 40km/hr
R.S = 120 - 80 = 40km/hr
time taken by van to catch up = 40/40 = 1 hr
ditance covered by car 1 x 120 = 120 km/h - time of day = 8:30 am + 1hr = 9:30 am
- time difference 8:30 am - 8:00am = 0.5hr
-
-
- reflection in line x = 0
- Rotation through -90° about (0,0)
- P'Q'R' and PQR , P"Q"R" and P'" Q'" R"',
PQR and P" Q" R", P'Q'R' and P'"Q'"R'"
-
-
- dy/dx = 3x2 - 4x
3x2 - 4x = 0
x(3x - 4)= 0
x=0
x = 11/3
y= (0)3 - 2(0)2 - 1=-1
(0, -1)
y = (4/3)3 - 2(4/3)2 - 1= -25/27
(11/3, -25/27) - (0, -1) maximum
(11/3, -25/27) minimum
- dy/dx = 3x2 - 4x
-
- when x = 1, gradient = 1
when x =1, y=-2
y+2 = -1
x -1
y + 2= -x + 1
Y= -x-1 - gradeint = 1
y + 2 = 1
x -1
y + 2 = x -1
y = x -3
- when x = 1, gradient = 1
-
-
-
-
- 2.7 ± 0.1 x 10 = 27km ± 1
- 306° ± 1°
9.6 ± 0.1 X 10= 96km ± 1 - 7.7 ± 0.1 x 10 = 77km ± 1
- 2.7 ± 0.1 x 10 = 27km ± 1
- (1/2 x 56 x 77)+ 1/2(77 + 27)14 = 2884km2
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE 2021 Westlands Mock Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students