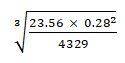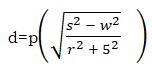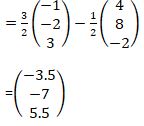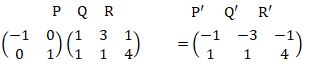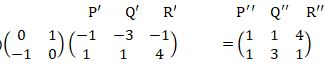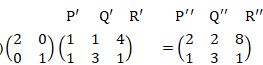Questions
INSTRUCTIONS TO CANDIDATES
- The paper consists of Two sections. Section I and Section II
- Answer ALL questions in Section I and any five questions in Section II
- Mathematical tables may be used except where stated otherwise.
- Candidates will be penalized for not following the instructions given in this paper.
SECTION I
- Use logarithms to 4 decimal places to evaluate (4 marks)
- Make s the subject of the formula (3 marks)
- Without using tables or calculator, evaluate and simplify (4 marks)
sin30 ° + sin45 °
cos 60 ° -1 - → →
Given the position vectors OA=4i +8j-2k and OB = 3k-i-2j. Point C divides vector AB in the ratio of 3:-1. Find the magnitude of OC. Give your answer to 2dp (3 marks) - Given that the values P=8.2 cm, A=4.1cm and B=7.0 cm were measured to 1dp. Find the percentage error in the evaluation of(3 marks)
K
A×B - Expand (1-1/2 x)10 upto the 4th term in the ascending powers of x. Hence evaluate the value of 0.9510 to 3 decimal places. (3 marks)
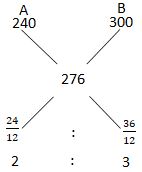
- Two types of coffee grade A and B retails at sh.240 and sh.300 respectively. Mohamed sell a mixture of both grades at shs.303 60, making a profit of 10%. Find the ratio in which he mixed the grades. (3 marks)
- Juma a form 2 student was told to pick two number x and y from a set of digits 0,1,2,3,4,5 and 6. Find the probability that the [x-y] is atleast 3. (3 marks)
- Two quantities x and y are such that y varies partly as the square of x and partly inversely as the square root of x. Given that when x=4,y=40 and when x=1,y=18. Find the value of y when x=0.25. (4 marks)
- In a triangle ABC, AB=7.2 cm, AC=6.8 cm and angle BAC=1200.
Calculate;- The length of BC to 3s.f (2 marks)
- If a circle passes through the vertices A, B and C. Find the radius of the circle. (2 marks)
- The table below shows income tax rates in a certain year
In that year Mr. Mogaka gets a total deduction of ksh5,000 he gets a personal tax relief of kshs.1056 and pays kshs.3944 for NHIF, WCPS and sacco loan repayment. CalculateMonthly income in Kshs Tax rate in each kshs 1 ≤x <9681
9681 ≤x< 18801
18801 ≤x < 27921
27921 ≤x < 37040
Over 3704010%
15%
20%
25%
30%- P.A.Y.E. (1 mark)
- Monthly income/salary (3 marks)
- Given that the matrix
maps a triangle A(0,0), B(2,1) and c(3,5) on to a straight line. Find the possible values of x. (3 marks)
- The 2nd, 10th and 42nd terms of an A.P forms the first three terms of a geometric progression, if the common differences of the AP=3. Find the sum of the first 10 terms of the G.p. (4 marks)
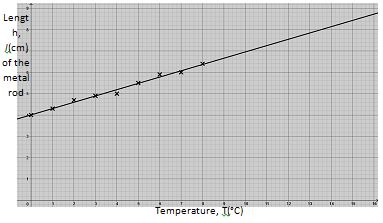
- Raw data collected from experimental observation normally have errors. Below is a table of results obtained results from an
experiment. The results show how length l(cm) of a metal rod various with increase in temperature T(0c).
Plot the values in the graph given below and draw the line of best fit.(2 marks)T(0C) 0 1 2 3 4 5 6 7 8 L(cm) 4.0 4.3 4.7 4.9 5.0 5.5 5.9 6.0 6.4 - Evaluate the value of x in the following trigonometric equation.
1/2 sin22x=+0.25 for--180° ≤x≤180° (3 marks) - The points with co-ordinates A(13,3) and B(-3,-9) are the end of a diameter of a circle centre 0. Determine ;
- The coordinates of 0 (1 mark)
- The equation of the circle expressing it in the form
x2+y2+ax +by +c=0 (2 marks)
SECTION II
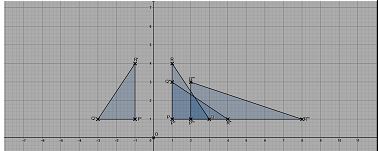
- The following are the vertices of a triangle PQR P(1,1), Q(3, 1) and R(1,4)
- Plot the triangle on the graph given (1 mark)
- Triangle PQR was reflected on the line x=0 to give P'Q'R'. Draw the triangle on the graph given.
- The triangle P'Q'R' was transformed by a matrix
to give P"Q"R". On the axes draw the triangle P"Q"R" on the grid. (2 marks)
- The triangle P"Q"R" was further transformed into a triangle P"'Q"' and R"' using the matrix
. Draw the triangle and state its coordinates (3 marks)
- Calculate the area of the triangle P"'Q"' R"' drawn above.(2 marks)
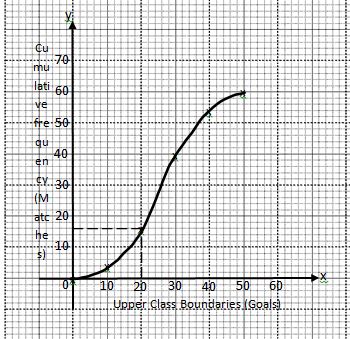
- The table below shows the number of goals scored in handball matches during a tournament
Number of goals 0 - 10 10 - 20 20 -30 30 -40 40 -50 Number of matches 2 14 24 12 8 - Draw a cumulative frequency curve in the space below. (3 marks)
- Find the probability of scoring at least 20 goals using your graph.(2 marks)
- Using an assumed mean of 25 calculate the standard deviation.(3 marks)
- Calculate the 6th decile (2 marks)
- Draw a cumulative frequency curve in the space below. (3 marks)
- Using a ruler and a pair of compasses only;
- Construct a triangle ABC such that AB=6cm, BC=8cm and angle ABC=600. (2 marks)
- On the same side of BC as A construct the locus of m such that angle BMC=600. (2 marks)
- Draw the locus of a point Q which is equidistant from B and C.(2 marks)
- Draw the locus of a point R such that RC=3cm. (1 mark)
- Draw the locus of a point P such that the area of triangle BPC=12cm2. (2 marks)
- Locate the region by shading such that; (2 marks)
Angle BMC ≥ 600, BQ ≥QC, RC<3 and area of BPC> 12cm2
-
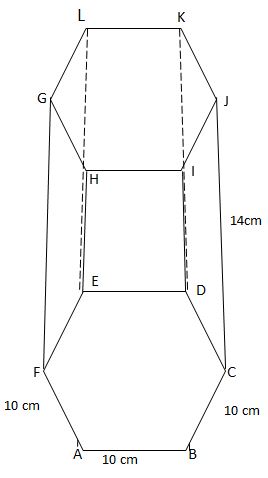
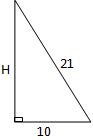
A B C D E F G H I J K L is a solid frustum which was cut two thirds way from the base of a regular hexagonal based pyramid of side 10cm. If the slant edge is 14cm. Calculate;- Perpendicular height of the pyramid (2 marks)
- Find the angle between the surface ABIH and ABCDEF (3 marks)
- Calculate the angle between HA and the base ABCDEF (2 marks)
- Calculate the angle between LK and BI (2 marks)
- An Aeroplane moves from point A to D via B and C
- Give the position of B if the plane moves due north from A(30os, 200W) to B covering a distance of 3600 nm. (2 marks)
- Calculate the distance from B to C along the parallel of latitude given that C lies on 500E. (2 marks)
- Calculate the shortest distance from C to D(300N, 1300 W) if the plane moves from C to D. (3 marks)
- Given that the plane left A at 0700h and stopped at B for 3 minutes and at C for 45 minutes. Calculate the day and time it will arrive at D. if the speed of the plane was 300knots (3 marks)
- Complete the table below for the function y=x^2-3x-4 (1 mark)
x -2 -1.5 -1.0 -0.5 0 0.5 1.0 1.5 2.0 2.5 3.0 y - Use the table and trapezoidal rule with 11 ordinate to estimate the area bounded by the curve y=x2-3x-4, x=-2, x=3 and x-axis (2 marks)
- Use the mid ordinate rule with 5 strips to estimate the area bounded by the curve y=x2-3x-4,x=-2,x=3 and x-axis (2 marks)
- Calculate the exact area above (3 marks)
- Find the percentage error involve in using the mid-ordinate role.(2 marks)
- A particle moves in such a way that the velocity V at any given time is v=10t – ½ t2 – 15/2 mls.
- Calculate the initial velocity (1 mark)
- Calculate the velocity when the time t=3 (2 marks)
- Find the displacement during the 5th second (4 marks)
- Calculate the maximum velocity attained (3 marks)
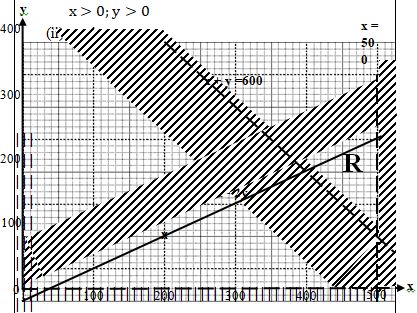
- The ministry of health made an order of both Astrazenica and Johnson and Johnson vaccines for a health centre. The total number of both vaccines should be more than 600 boxes. The number of boxes of Johnson and Johnson should be less than 500 boxes and more or equal to twice the number of Astrazenica. Letting x to represent the number of Johnson and Johnson boxes and y – to represent the number of boxes of Astrazenica.
-
- Form all the in equalities in x and y to represent the above information. (3 marks)
- Represent the inequalities on a graph (4 marks)
- If the cost of importing 1 box of Johnson and Johnson is sh1000 and astrazenica is shs.800. Find maximum cost of importing the vaccines. (3 marks)
-
Marking Scheme
-
Number Logarithm Working 23.56
0.2821.3721
+1.89441.4472
+1.44720.2665
- 3.63642.8944 4329 4.6301 4/3 - 2 + 2.6301/3 7.528 x 10-2 2.8767 2.8767 =0.007528 - d2 = p2 (5² - w²)
r² + s²
d²(r²+s²)=p²(s²-w²)
d²r² + d²s² = p²s² - p²w²
p²s² - d²s² = d²r² + p²w²
s²(p² - d²)= (d²r² + p²w²)
√s² = √(d²r² + p²w²)
(p² - d²)
s= ± √(d²r² + p²w²)
(p² - d²) - Sin 30 = ½
Sin 45 = √2/2 Cos 60 = √3/2
= 1/2 + √2/2
√3/2 - 1
1 + √2
2
√3 - 2
2
1 + √2 x √3 + 2
√3 - 2 √3 +2
-√3 + 2 + - √6 + 2√3
3 - 4
√3 - 2 - √2√3 - 2√3 - OC= 3/2 OB- 1/2OA
|OC| = √(3.52 + 72 + 5.52)
=9.57 units (2d.p) - RE(P/AB) = RE(P) + RE(A) + RE(B)
= 0.05 + 0.95 + 0.05
8.2 4.1 4.1
=0.030488
%error= 0.030488 x 100% = 3.0488 - (1 - 1/2x)10 = 1 -10(1/2x) + 45(1/2x)2 - 120(1/2x)3
= 1-5x+ 45/4(0.1)2 - 15(0.1)3
=0.5975
=0.598 - 110% → 303.60
110% → 100/110 x 303.60 = 276 -
x\y 0 1 2 3 4 5 6 0 0 -1 -2 -3 -4 -5 -6 1 1 0 -1 -2 -3 -4 -5 2 2 1 0 -1 -2 -3 -4 3 3 2 1 0 -1 -2 -3 4 4 3 2 1 0 -1 -2 5 5 4 3 2 1 0 -1 6 6 5 4 3 2 1 0 - y=kx2 + m/√x
80 = 32k + m
18=K+M
62 = 31k
k=2, m=16
y= 2(0.25)3 + 16/0.5
y= 0.125 + 32
y= 32.125 -
- BC2 = 7.22 + 6.82 - 2 x 7.2 x 6.8 Cos 120° = √147.04
BC = 12.13cm ≅ 12.1cm - 12.1 = 2R
Sin 120°
radius = 6.986cm
- BC2 = 7.22 + 6.82 - 2 x 7.2 x 6.8 Cos 120° = √147.04
-
- PAYE = 5000 -(3944)= 1056
- Gross tax = 1056 + 1056= 2112
SLABS
9680 x 10/100 = 986
= 1144
= 2112
x x 15/100
x = 1144/0.15 = 7626.67
monthly income = 9680 + 7626.67
= Ksh 17306.70
- -9x - x2 + 6x=0
-x2 - 3x =0
x2 + 3x =0
x(x+3)=0
x=0 qx=-3 -
- a + 27 = a + 123
a + 3 a + 27
a2 + 54a + 729 = a2 + 126a + 369
72a = 360
a= 5
r = 32/8 = 4
S10 = 8(4¹⁰ - 1)
4-1
= 2, 796, 000 - 2(1/2 Sin22x = -0.25)
Sin22x = 0.25 x 2 = 0.5
Sin 2x = √(0.5 = ± 0.7071)
Sin 2x = Sin - 135, Sin - 45, Sin 45, Sin 135
= sin- 315, Sin - 225, Sin -135, Sin 225
2x = -135, -45, 45, 135, -315, -225, +225, 315
x = 67.5, 22.5, 22.5, 67.5, -157.5, 112.5, 157
x = -157.5, 67.5, -22.5, 67.5, 112.5 and 157.5 -
- Center 0 ( x₁ + x₂ , y₁ + y₂ )
2 2
= ( 13 +- 3 , 3 +- 9 ) = (5, 3)
2 2 - Equation of circle
→
|OA| = √82 + 62 = 10 units
Equations
(x - 5)2 + (y-3)2 = 102
x2 - 10x + 25 + y2 + 6y + 9 = 100
x2 + y2 - 10x + 6y + 25 + 9 - 100 = 0
x2 + y2 - 10x + 6y - 66 = 0
- Center 0 ( x₁ + x₂ , y₁ + y₂ )
-
- ΔPQR drawn
-
⇒P'(-1,1), Q' (-3, 1), R'(-1,4) -
⇒P''(1,1), Q'' (1,3), R''(4,1) -
⇒P'''(2,1), Q'''(2,3), R'''(8,1) - A = 1/2 x 6 x 2
= 6 square units
- ΔPQR drawn
-
-
-
- P(> 20)= 45/60 or 3/4
-
-
S = √(6600/60) - (100/60)2class f x d= x- 25 d2 fd fd2 0-10 2 5 -20 400 -40 800 10-20 14 15 -10 100 -140 1400 20-30 24 25 0 0 0 0 30-40 12 35 10 100 120 1200 40-50 8 45 20 400 160 3200 Σf = 60 Σfd=100 Σfd2= 6,600
= 10.35481638 - L + [⁶/₁₀ N - cf] x i
f
20 + [36 -16/24] x 10
= 281/3
-
-
- LSF = 1/3
L = 14 x 3= 21cm
H = √212 - 102= 18.47cm - h = √(212 - 52)
= 20.40cm
θ = Sin-1 (18.47/20.40)
= 64.88° -
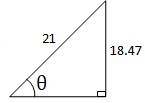
θ = Sin-1 (18.47/21)
= 61.58° -
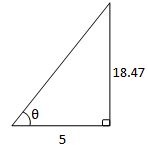
θ = tan-1 (18.47/5)
= 74.85°
or 180° - 74.85° = 105.2°
- LSF = 1/3
-
- 60 x θ = 360
60 60
θ = 60
60° - 30° = 30°
→B(30°S, 20°W) - θ = 50° + 20° = 70°
BC = 60 x 70 Cos 30°
= 3637.3nm - 180 - 2 x30 = 120°
CD = 60 x 120
=7200nm - 7200
3637.3
14437.3
Travel time = 14437.3
300
= 48hrs 7min
Long dif in time = (70 x 4/60) - (180 x 4/60)
= 7hrs 20 mins behind
48 hrs 07 min - 7hrs 20 min + 7hrs = 47hrs 47 min
⇒47hrs 47 min - 24hr = 2347hrs the next day
or 11:57pm the next day
- 60 x θ = 360
-
y= x2 - 3x - 4
x -2 -1.5 -1.0 -0.5 0 0.5 1.0 1.5 2.0 2.5 3.0 y 6 2.75 0 -2.25 -4 -5.25 -6 -6.25 -6 -5.25 -4.0 - A = 1/2h ((y0 + y11) + 2(y1 + y2 + y3 + y4 ----+ y10)
A= 1/2 x 0.5 [(6+4) + 2(2.75 + 0 + 2.25 + 4 + 5.25 + ...)]
= 0.25 (10 + 75.5)
= 21.375 square units - A= h[y1 + y2 + y3 + y4 ------ + y5]
A= 1[2.75 + 2.25 + 5.25 + 6.25 + 5.25]
= 21.75 square units - A = ∫-1-2 (x2 - 3x -4 )dx + ∫3-1 (x2 = 3x -4)dx
=[x³/3 - 3x²/2 - 4x ]-1-2 + [x³ - 3/2x2 - 4x]3-1
=[((-1)³/3 - 3/2(-1)2 -4(-1)) - ((-2)³/3 - 3/2(-2)2 - 4 (-2)) + ((3)³/3-4(-1))]
(25/6) + (182/3)= 211/2 or 21.5 square units - (|21.75 - 21.5|) x 1
21.5
- A = 1/2h ((y0 + y11) + 2(y1 + y2 + y3 + y4 ----+ y10)
- V= 10t - 1/2t2 - 15/2
- V= 10(0) - 1/2(3)
= -7.5mls - V= 10t - 1/2t2
V= 10(3) - 1/2(0)2 - 15/2
=18m/s - s= ∫54 (10t - 1/2t2 - 15/2)dt
s= [10t²/2 - t³/6 - 15/2t + c]54
s =[ 5t2 - t³/6 - 15/2t + c]54
s= [(5(5)2 - (5)³/6) - 15/2(5)) - (5(4)2 - (4)³/6 - 15/2(4))]
[(662/3) - (301/3)]
= 271/3 - a = dv/dt = 10-t
10-t = 0 ⇒t=10
V=10(10) - 1/2(10)2 - 15/2
= 42.5mls
- V= 10(0) - 1/2(3)
-
-
- x + y > 600
x<5000
x> 2y
x> 0:y>0 -
- x + y > 600
- objective function: 1000x + 800y
(480, 240)(495, 245)(499, 249)
→ 1000(480) + 800(240) = Ksh 672,000
→ 1000(495) + 800(245) = Ksh 691,000
→ 1000(499) + 800(249) = Ksh 698,200
Hence , max cost = 698,200
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 2 Questions and Answers - KCSE 2021 Westlands Mock Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students