Mathematics Paper 2 Questions and Answers - Butere Mock Exams 2021

INSTRUCTIONS TO CANDIDATES

1. Write your name, stream, admission number and index number in the spaces provided above.
2. The paper contains two sections, Section I and II
3. Answer all questions in section I and ONLY any FIVE questions from section II.
4. All answers and working must be shown on the question paper in the spaces below each question
5. Show all steps in your calculations, giving answers at each stage
6. Marks may be given for each correct working even if the answer is wrong
7. Non-programmable silent electronic calculators and KNEC mathematical tables may be used.

SECTION I
Answer all the questions in the spaces provided (50 marks)

1. The expression x² + 10x + c + 2 = 0 is a perfect square. Find the value of c if it is a scalar. (2mks)
2. Muya was asked to truncate ⁷/₉ to 3 significant figures. He rounded it off instead to 3 decimal places. Calculate the percentage error resulting from his rounding off. (3mks)
3. The co-ordinates of a point A is (2, 8, 3) and B is (-4, -8, -5). A point P divides AB externally in the ratio 7: -3.
   Find the co-ordinates of P (3mks)
4. In a triangle XYZ, XY = 2cm, YZ (2√3-1) cm, and angle YXZ = 60º. Determine Sine XZY giving your answer in the form
   m + √3, where M and N are integers (4mks)
       n
5. Find the independent term of x in the expansion of (x³ – ²/X³)⁶ (3mks)
6. Solve for x: (log₃x)² – ½ log₃ x= ³/₂ (3mks)
7. The cash price of a T.V set is Ksh.13,800. Walter opts to buy the set on hire purchase terms by paying deposit of Ksh.2,280. If simple interest of 20% p.a is charged on the balance and the customer is required to pay by monthly installments for 2 years, calculate the amount of each installment. (3mks)
8. Make x the subject of the formula ax = ^3r/₂ - ^x2/₂ (3mks)
9. Calculate the area under the curve y = 3x² + 8 and bounded by lines; y = 0, x = 1 and x = 6, using the mid-ordinate rule with 5 strips. (3mks)
10. A circle is tangent to the y – axis and intersects the x- axis at (2,0) and (8,0). Obtain the equation of the circle in the form x² + y² +ax +by +c = 0, where a, b and c are integers (4mks)
11. A variable y varies as the square of x and inversely as the square root of z. Find the percentage change in y when x is changed in the ratio 5:4 and z reduced by 19% (3mks)
12. Solve for X in the equation:
    2 Sin²x – 1 = Cos²x + Sin x, for 0º ≤ x ≤ 360º (3mks)
13. A die is biased so that when tossed, the probability of a narrator of a number n showing up, is given by p(n) = kn where k is a constant and n = 1, 2, 3, 4, 5, 6 (the numbers of the faces of the die)
    1. Find the value of k (1mk)
    2. If the die is tossed twice, calculate the probability that the total score is 11 (2mks)
14. In the figure below, the tangent ST meets chord VU produced at T. Chord SW passes through the Centre, O of the circle and intersects chord VU at X. Line ST = 12cm and UT = 8cm.
    
    
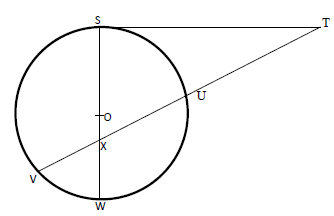
    1. Calculate the length of chord VU (1mk)
    2. If VX : XU = 2 : 3, Find SX (2mks)
15. Dota measured the heights in centimeters of 104 trees seedlings are shown in the table below
    

    Height	0 - 19	20 - 29	30 - 39	40 - 49	50 - 59	60 - 69	70 - 79
    No. of Seedlings	9	16	19	26	20	10	4

    Calculate the quartile deviation (4mks)
16. Given that the ratio x:y = 2:3, find the ratio (5x – 2y) : (x +y) (2mks)

SECTION II
Answer ONLY five questions in this section (50 marks)

17. A curve is represented by the function, y = 2x³ + 3x²
    1. Find:
       1. the x-intercept of the curve (2mks)
       2. the y-intercept of the curve (1mk)
    2.      
       1. Determine the stationary points of the curve of the curve (3mks)
       2. For each point in b(i) above, determine if it is maximum or minimum (2mks)
    3. Sketch the curve in the space below (2mks)
18. Use ruler and a pair of compasses only in this question
    1. Construct;
       1. triangle ABC in which AB = 8.5cm, BC = 7.5cm and <BAC = 30º and <ABC = 105º (3mks)
       2. a circle that passes through the vertices of triangle ABC. Measure the radius (3mks)
       3. the height of triangle ABC with line AB as the base. Measure the height. (2mks)
    2. Determine area of the circle that lies outside the triangle (2mks)
19.      
    1. Complete the table below, giving your values to 2 decimal places (2mks)
       

       x	0	30	60	90	120	150	180	210	240	270	300	330	360
       (2cos x) -1			0		-2		-3		-2	-1	0		1
       Sin x	0			1		0.50	0			-1			0

    2. Draw the graph of y= (2 cos x) – 1 and y=sin x on the grid provided below. Use the scale 1cm represent 30º horizontal 2 cm represent 1 unit vertically and 2cm for 1 unit on the y-axis (4 mks)
       
    3. Use the graph to solve:
       1. (2cos x) – 1 = -1.5 (1mk)
       2. 2 cos x – sin x =1 (2mks)
    4. State the amplitude of the wave y=2cos x – 1 (1mk)
20. A bag contains blue, green and red pens of the same type in the ratio 8:2:5 respectively. A pen is picked at random without replacement and its colour noted.
    1. Determine the probability that the first pen picked is
       1. Blue (1mk)
       2. Either green or red. (2mks)
    2. Using a tree diagram, determine the probability that
       1. The first two pens picked are both green (4mks)
       2. Only one of the first two pens picked is red. (3mks)
21. A and B are two points on the earth’s surface and on latitude 30ºN.The two points are on the longitude 40ºW and 104ºE respectively.
    Calculate
    1.      
       1. The distance from A to B along a parallel of latitude in kilometres. (3mks)
       2. The shortest distance from A to B along a great circle in kilometre (4mks)
          (Take π = ²²/₇ and radius of the earth =6370km)
    2. If the local time at B is 8.00am, calculate the local time at A (3mks)
22. Lengths of 100 mango leaves from a certain mango tree were measured t the nearest centimeter and recorded as per the table below,
    

    Length in cm	9.5-12.5	12.5-15.5	15.5-18.5	18.5-21.5	21.5-24.5
    No. of Leaves	3	16	36	31	14
    Cumulative frequency

    1. Fill in the table above. (2 mks)
    2. Draw a cumulative frequency curve from the above data. (3 mks)
    3. Use your graph to estimate
       1. The quartile deviation of the leaves (3mks)
23. The number of leaves whose lengths lie between 13cm and 17cm. (2mks)
24. Use the trapezium rule with 7 ordinates to estimate the area enclosed by the curve y=½x²+3 and the lines x = 0, x = 6 and the x-axis. (4 mks)
25. Determine the exact area bounded the curve and the lines in section a) above (3 mks)
26. Calculate the percentage error from the trapezoidal rule (3 mks)
27. A manufacturer sells two types of books X and Y. Book X requires 3 rolls of paper while Book Y requires 2½ rolls of paper. The manufacturer uses not more than 600 rolls of paper daily in making both books. He must make not more than 100 books of type X and not less than 80 of type Y each day
28. Write down four inequalities from this information (4mks)
29. On the grid provided, draw a graph to show inequalities in (a) above (3mks)
30. If the manufacturer makes a profit of sh 80 on book X and a profit of sh 60 on book Y, how many books of each type must it make in order to maximize the profit. (3mks)

MARKING SCHEME 

1. b² = 4ac
   5² = c + 2
   25 = c + 2
   c = 23
   M1
   A1
   Correct expression in C
   02
2. Truncated = 0.777
   Rounded off = 0.778
   A.E = 0.778 – 0.777 = 0.001
   % E = x 100
   = 0.12870012870012870012870012870013
   B1
   M1
   A1
   For both values correct
   Expression for % Error
   Allow 0.1287
   03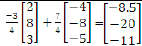
3. 
   
   P(-8.5, -20, -11)
   M1
   A1
   B1
   Expression
   Correct matrix
   Co-ordinate form
   03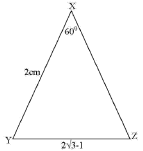
4. 
     2   = 2√3 - 1
   sinZ    sin60
     2   = 2√3 - 1
   sinZ    ^√3/₂
   sinZ =   √3     x 2√3 + 1
             2√3 - 1    2√3 + 1
   sinZ = 6 +√3
                11
   M1
   M1
   M1
   A1
   Correct substitution in sine rule
   Surd form for sin 600
   Correct attempt to rationalize
   CAO
   04
5. (x³)⁶ -6 (x³)⁵ + 15 (x³)⁴ (²/_x3)² - 20 (x³)³(²/_x3)³
   - 20 (x³)³(²/_x3)³
   - 20 x 8 = - 160
   M1
   M1
   A1
   Expansion up to the 4th term
   Correct attempt to simplify
   Constant term stated
   03
6. Let log₃x = y
   2y² – y – 3 = 0
   (2y – 3)(y + 1) = 0
   y = -1 or y = 1 ½
   if log₃x = -1, x = 3-1 = ¹/₃
   if log₃x = 1½ , x = 31.5 = 5.196
   M1
   A1
   B1
   Quadratic equation formed
   For both correct
   For both correct
   03
7. P = cp – d = 13800 – 2280 = 11520
   I = 11520 x 20 x 2/100= 4608
   A = P + I = 11520 + 4608 = 16128
   MI= 16128 ÷ 24
   = 672
   M1
   M1 A1
   Expression for simple interest
   Expression for MI
8. 2ax + x² = 3v
   x²  + 2ax – 3v = 0
   x² + 2ax +a² = 3v + a²
   √(x + a)2 = √(3v +a² )
   x + a = ±√(3v +a² )
   x = -a ± √(3v +a² )
   M1
   M1
   A1
   Formation of quadratic equation
   Completing the square
   Correct attempt to solve
   03
9.      
   

   x	1.5	2.5	3.5	4.5	5.5
   y	14.75	26.75	77.75	68.75	98.75

   A= 1(14.75 +26.75+77.75+68.75+98.75)
   = 253.75 square units
   B1
   M1
   A1
   Correct values of mid-ordinates
   Expression for area
   03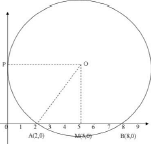
10. 
    M(2 + 8 , 0 + 0) = M(5,0)
           2         2 
    OA = OP = 5 units
    AM = 5 – 2 = 3 units
    OM = √(5² – 3² ) = 4 units
    C(5,4) , r = 5
    (x – 5)² + (y – 4)² = 52
    x² – 10x + 25 + y² – 8y + 16 = 25
    x² + y² -10x - 8y + 16 = 0
    M1
    M1
    M1
    A1
    Expression for midpoint
    Radius, r
    Expression for OM
    Correct substitution
    Correct expanded form
    04
11. y = kx²
         √z
    y₁ =kx(⁵/₄)² 
          √0.81
    = 1.736k
    % change =1.736 - 1 x 100
                            1
    = 73.6%
    M1
    M1
    A1
    Correct substitution
    Expression for percentage change
    03
12. 3sin²x – sin x – 2 = 0
    Let sin x = y
    3y²- y -2 = 0
    (3y + 2)(y – 1 ) = 0
    y = 1 or y = ^-2/₃
    sin-1(1) = 90º
    sin-1(-2/3) = 221.8º, 317.8º
    x = 90º, 221.8º, 317.8º
    M1
    M1
    A1
    B1
    Quadratic equation formed
    Correct attempt to solve
    For both
    All values correct
    04
13.           
    1. k + 2k + 3k + 4k + 5k + 6k = 1
       21k = 1
       k = ¹/₂₁
    2. P(5&6) 0r P(6&5)
        60 
       441
       B1
       M1
       A1
       Addition of probabilities (allow for any correct)
       Allow ²⁰/₁₄₇
       03
14.         
    1. Let VU = x
       8(8 + x) = 12²
       8x = 144 – 64 =80
       x = 10
    2. VX = ²/₅ x 10 = 4
       XU = ³/₅ x 10 = 6
       XT = 6 + 8 = 14
       SX = √(14² – 12²) = 7.211
       B1
       M1
       A1
       x = 10
       Expression for XT
       03
15.      
    

    h	10-19	20-29	30-39	40-49	50-59	60-69	70-79
    f	9	16	19	26	20	10	4
    cf	9	25	44	70	90	100	104

    Q₁ = 19.5 + 26 - 9 x 10 = 20.5625
                          26
    Q₃ = 49.5 + 78 - 70 x 10 = 53.5
                            20
    Quartile deviation = 53.5 - 20.5625 = 16.46875
                                               2
    B1
    M1
    M1
    A1
    Cf
    Q1 and Q3
    Expression for quartile deviation
    Allow 16.47
    04
16. ^x/_y = ²/₃
    x = ²/₃y
    5(²/₃y) - 2y(²/₃y) + y₁
    (⁴/₃y):(⁵/₃y) = 4:5
    M1
    A1
    Correct substitution
    02
17.        
    1.         
       1. x-intercept
          x²(2x + 3) = 0
       2. y-intercept
          When x =0, y = 0
    2.      
       1. Stationary points of curve = 0
          ^dy/_dx=6x²+ 6x = 0
          6x (x + 1) = 0
          x = 0 or x = -1
          stationary points (0,0) and (-1,1)
       2.    
          

          x	-2	-1	-0.5	0	1
          dy/dx	12	0	-1.5	0	12
          sketch

          maximum point (-1, 1), minimum point (0,0)
          M1
          A1
          B1
          M1
          A1
          B1
          B1
          B1
          B1
          Factorized form
          Both correct
          Both correct
          Derivative equated to zero
          Attempt to solve
          For both
          Checking points
          For both
          B1
          B1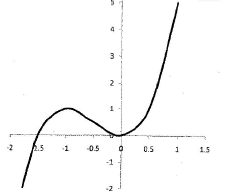
       3. 
          Points plotted (-1.5,0), (-1,1), (0,0)
          Smooth curve
18.      
    1.         
       1.    
             
       2. r = 5.2cm ± 0.1
       3. h = 5cm ± 0.1
    2. area of circle – area of triangle
       = 84.98 – 21.25
       = 63.73cm²
       B1
       B1
       B1
       B1
       B1
       B1
       B1
       B1
       M1
       A1
       Construction of 300
       Construction of 1050
       Complete triangle, well labeled
       Line bisectors
       Complete Circle drawn radius
       height dropped
       follow through for r and h ± 0.1
       10
19.      
    1.   
       

       x	0	30	60	90	120	150	180	210	240	270	300	330	360
       2cosx-1	1	1.73		-1		-2.73		-2.73			B1	0.73	1
       sinx		0.50	0.87		0.87			-0.50	-0.87		-.087	0.50	0

    2.      
       
    3.      
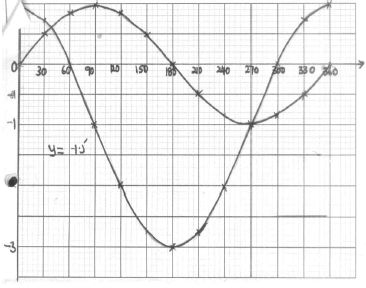
       1. x = 102º or 253.5º ± 1.5
       2. 2cos x -1 = sin x
          x = 37.5º or 270º ± 1.5
       3. Amplitude = 2
          B1
          S1
          P1
          C1
          C1
          B1
          B1
          B1
          B1
          Scale
          Plotting for both
          Smooth curve
20.        
    1.    
       1. ⁸/₁₅
       2. 2 + 5 = 7 
           15      15
          
    2.      
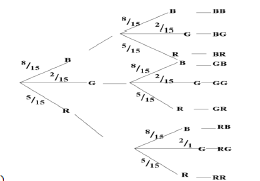
       1. (⁸/₁₅ x ⁵/₁₅) + (⁸/₁₅ x ⁵/₁₅) + (²/₁₅ x ⁸/₁₅) + (²/₁₅ x ⁵/₁₅)
          (⁵/₁₅ x ⁸/₁₅) + (⁵/₁₅ x ²/₁₅) = ¹³²/₂₂₅
       2. P(BR) + P(GR) + P(RB) + P(RG)
          (⁸/₁₅ x ⁵/₁₅) + (²/₁₅ x ⁵/₁₅) + (⁵/₁₅ x ²/₁₅) + (⁵/₁₅ x ²/₁₅) = ¹⁰⁰/₂₂₅
          B1
          M1
          A1
          B1
          M1
          M1
          M1
          A1
          M1
          M1
          A1
          Tree diagram draw with probabilities indicates
          1 probability
          Addition of the probability
          probability
          Addition
21.      
    1. Distance =  a  2πRcosθ
                        360
       a=longitude difference
       =40+140=180º
       180 x 2 x 22 x 6370cos30
       360          7
       =17,337.8Km
    2. θ=60 x 2
       =1200
       Distance =  θ   2πR
                        360
       =120 x 2 x 22 x 6370
          360          7
       =13,346.7km
    3. A(30ºN,40ºN)
       B(30ºW,140ºE)
       Difference in longitude=140+40
       =180º
       1º = 4min
       180=?
       180 x 4 = 720minutes
       720 = 12hrs
        60
       8.00 + 12.00 = 20.00
       =12.00hrs/8.00pm
       10
       B1
       M1
       A1
       M1
       A1
       M1
       A1
       M1
       M1
       A1
       For 180º
       10
22.    
    1. 
       

       Length in cm	9.5-12.5	12.5-15.5	15.5-18.5	18.5-21.5	21.5-24.5
       No. of leaves	3	16	36	31	14
       cf	3	19	55	86	100

    2.      
           
    3.      
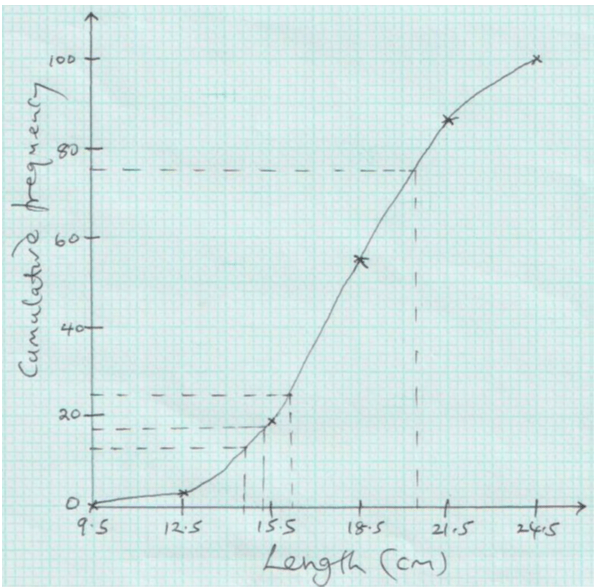
       1. Q₃ = 19.25, Q₁ = 17.15
          ½ (Q₃ – Q₁) = ½ (19.25 – 17.15)
          = 1.05
       2. 13cm - - 15.2, 17cm - - 15.8
          15.8 – 15.2 = 0.3
          B2
          B1
          S1
          P1
          C1
          B1
          M1
          A1
          B1
          B1
          All values correct
          At least 4 values correct
          Q3 & Q1 correct
          Correct cf values
          10
23.      
    

    x	0	1	2	3	4	5	6
    y	3	3.5	5	7.5	11	15.5	21

    A = [(3 + 21) + 2(3.5 + 5 + 11 + 15.5)]
    = 0.5[24 + 85]
    = 54.5 sq.units
    
    B2
    M1
    A1
    M1
    M1
    A1
    B1
    M1
    A1
    10
24.    
    1. x ≤ 100
       y ≥ 80
       x ≥ 0
       3x + 2½y ≥ 600
       B1
       B1
       B1
       B1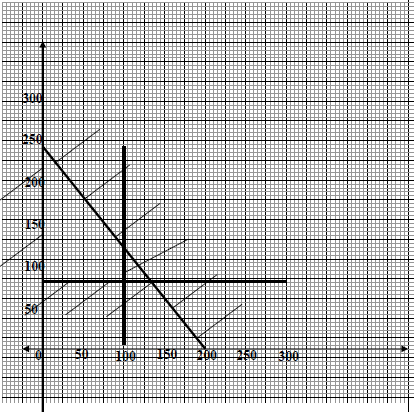
    2. 
       
       For each correct inequality
    3. Objective function p = 80x + 60y
       x = 200
       y = 120
       B1
       B1
       B1
       B1
       B1
       B1
       For each correct line drawn