Instructions to candidates
- This paper consists of two sections. Section 1 and section II
- Answer ALL question in section I and only five question from section I
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematics tables may be used

QUESTIONS
SECTION1
ATTEMPT ALL THE QUESTIONS IN THIS SECTION
- Without using mathematical table or caleulator, evaluate
√0.84x 1.23 (3mks)
2.87 - Simplify leaving your answer in form of ab
3√2 x 32t ÷ 2- 2t x 3t (3mks) - The original price of a box is ksh Q. when the price was increased in the ratio 53:19, the new price become ksh (Q+ 1802). Calculate Q. (3mks)
- Solve Sin(3A - 15)º = Cos(2A + 60)º, hence find tan (A +21)h correct to 4 significant figures (3mks)
- The interior angles of an irregular octagon are (x -33)º, 153º, 149º, (1/2x + 45)º, (1/3x+ 153)º, (125-1/6x)º and (5/6x+110)º. Determine the value ofx. (3mks)
- Use the logarithm tables to evaluate 0.19 x 0.6401 Correct to 4 significant figures. (4mks)
13.5 x 0.8988 - Threc boats P, Q and R are situated in such a way that boat Q is 4.5km on a bearing of 120º from boat P. Boat R is 6km on a bearing of 030º from Q. Calculate the distance of boat R from boat P. (3mks)
- Simplify the expression 4x2-9x2 (3mks)
3x2-4xy-42 - In the figure ABCD shown below a parallelogram, AB=12cm and angle DAB=48
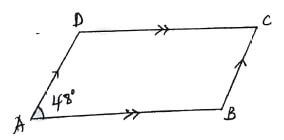
The area of the parallelogram is 36 cm', find the perimeter correct to 2 decimal places. (4mks) - Find the integral values of x which satisfies the incqualities
2x 1< 7+x ≤ 3x + 1 (3mks) - Use reciprocal and cube tables to evaluate 9 - 25000 correct to 2 significant figures (3 mks)
96.96 (69.96)3 - At the end of her stay in Kenya a French tourist had 3420 French Frances which she decided to change to Euros. Given that the exchange rate was
1 French France ksh.1 1.25
1 Euro = ksh. 72.50
Calculate the number of Buros she received if the bank charged her 2% commission to the nearest Euro. (3mks) - Three light signals have been set to flash at intervals of 15 minutes, 20 minutes and 24 minutes. If they all flash together at 1015hours, when will they next flash together? (3mks)
- Two successive translation (3 a) and (b b) respectively are the same as (8 15)
Detemine the product of a and b. (3mks) - Two similar solids have masses of 512g and 125g. The base area of the larger solids 192cm'. Find the area of the smaller solid. (3mks)
- A pick-up is loaded with a mixture of bags ofmaize and bags of beans. One bag of maize has a mass of 90kg and one bag of beans has a mass of 70kg. The pick-up is loaded with 300 bags whose total mass is 23.4 tonnes. Find the number of bags of each type it is carrying. (3mks)
- A (2, 5), B (9, 12) and C (x, y) are vertices of a triangle.
- Find the equation of line AB in the form ax + by = c (3mks)
- Find the equation of the perpendicular bisector of line AB (3mks)
- Given that AC is perpendicular to AB and the equation of the line BC is y = -2x + 30
Find the coordinate of C (4mks)
- In the figure below (not drawn to scale) AB=8.5cm, AC=7.2cm, AD=7.8cm. CD=3.8 and angle CAD=48.2°
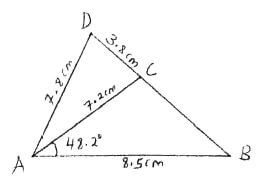
Calculate to 2 decimal places- The length BC (3mks)
- The size of angle ABC (2mks)
- The size of angle CAD (3mks)
- The radius of a circle that passes through the vertices of triangle ABD (2mks)
- The height of 50 seedlings in a nursery were measured to the nearest centimeters and recorded as shown below
25 23 33 29 34 25 23 31 37 31
31 28 16 23 21 36 32 36 42 40
35 22 21 27 30 19 34 27 38 22
32 31 28 29 24 20 29 35 17 15
28 40 32 27 26 23 20 32 26 28- Make a grouped frequency table with a class width of5 starting with 15 (3mks)
- Calculate to 2 decimal places
- The mean height (4 mks)
- The media height (3mks)
- Two towns P and Q are 580km apart. A bus left town P at 6.10am and maintains an average speed of 90km/h between P and Q. A car left Q at 8:00am and travelled towards P at an average specd of 120km/h.
-
- How far from town P did they meet? (4mks)
- At what time did they meet (4mks)
- A rally driver starts from Q towards town P at 10:00am. If its average speed was 180km/h. Calculate
- The time taken for the rally driver overtook the car (4mks)
- The time when the rally driver overtook the car (1mk)
-
- A triangle ABCD with vertices A(1,1), B(3,-1) and C(4,2) is mapped unto triangle A'B'C' with vertices A'(-l,-1), B'(1,-3) and C' (-2,-4).
- On the grid provided draw triangle ABC and A' B'C (Zmks)
- Describe the transformation that maps ABC unto A'B'C (2mks)
- A'BC" is the image of A'B'c' under negative quarter turn about the origin. Draw the triangle A "B"C'" and state the coordinates. (2mks)
- ABC is mapped unto A'"B"'C''' by an enlargement center (0, 2) and scale factor -2.
Draw ABlc (2mks) - Given that the area of triangle ABC is 7.5cm2. Calculate the area of triangle A'''B'''C''' (2mks)
-
- Given that the matrix
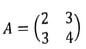 . Find A . (2mks)
. Find A . (2mks) - Moi Siongiroi Girls' bought 200bags of sugar and 300 bags of rice for a total cost of ksh.850000. Tenwek boys' bought 90 bags of sugar and 120 bags of rice at a total of ksh.360000 from the same store as Moi Siongiroi Girls'. If the price of a bag of sugar is ksh. X and that of rice is ksh. Y.
- Fom a matrix equation to represent the above information (2mks)
- Use the matrix A" to fine the price of one bag of each item (3mks)
- Kipsigis Girls' bought 225 bags of sugar and 360 bags of rice from the same store. The school was given a total discount of ksth. 33,300. If the discount on the rice of a bag of rice was 2%. Calculate the percentage discount on the price of a bag of sugar. (3mks)
- Given that the matrix
- The figure below represents a conical flask. The flask consists of hemispherical top lid cylindrical neck, frustum part and hemispherical base. The vertical height of the flask is 21 cm. The diameter of the cylindrical part is 4cm while that of the conical base is 10 cm.
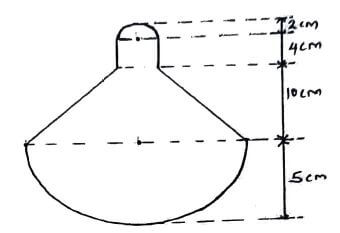
Calculate, correct to 1 decimal places- The slanting height of the frustum part (2mks)
- The slant height of smaller cone that was cut off to make the frustum part (2mks)
- The external surface area of the flask (take T=3.142) (4mks)
- The mass of the liquid in the hemispherical base is 204g. find the density of the liquid. (2mks)
- Using a ruler and a pair of compasses only, construct,
-
- Triangle ABC in which AB-Scm, <BAC=30º and <ABC=105º (3mks)
- A circle that touches line AC produced, AB produced and line BC. Measure the radius. (3mks)
- Drop a perpendicular line from pointB to meet AC at R. measure BR (2mks)
- Determine the area of triangle ABC (2mks)
-

MARKING SCHEME
SECTION1
ATTEMPT ALL THE QUESTIONS IN THIS SECTION
- Without using mathematical table or caleulator, evaluate
√0.84x 1.23 (3mks)
2.87
0.84 x 1.23 x 100
2.87 x 10000
=√ 36
100
= 6/10
= 3/5 or 0.6 - Simplify leaving your answer in form of ab
3√2 x 32t ÷ 2- 2t x 3t (3mks)
[(2t ÷ 2-2t) x (32t x 3t)]1/3
= [23t x 33t]1/3
= 2t x 3t
= 6t - The original price of a box is ksh Q. when the price was increased in the ratio 53:19, the new price become ksh (Q+ 1802). Calculate Q. (3mks)
53 Q = Q + 1802
19
34 Q = 1802
19
Q = 1802 x 19
34
= sh 1007
OR
53 = Q + 1802
19 9 - Solve Sin(3A - 15)º = Cos(2A + 60)º, hence find tan (A +21)h correct to 4 significant figures (3mks)
(3A - 15)º + (2A + 60)º = 90º
5A + 45º = 90º
5A = 45º
A = 9º
Tan (9 + 21)º
= tan 30º
= 0.5774 - The interior angles of an irregular octagon are (x -33)º, 153º, 149º, (1/2x + 45)º, (1/3x+ 153)º, (125-1/6x)º and (5/6x+110)º. Determine the value ofx. (3mks)
S8 = 90(2 x 8 - 4) = 1080º
(x - 33)º + 153º + 149º + (1/2 x 45)º + (1/3x + 153)º + (125 - 1/6x)º + (5/6x + 110)º = 1080º
3.5x + 870 = 1080º
3.5x = 210º
x =60º - Use the logarithm tables to evaluate 0.19 x 0.6401 Correct to 4 significant figures. (4mks)
13.5 x 0.8988
NO (sp) log 1.9 x 10-1 1.2788 + cos 50.2 º
6.401 x 10-11.8063 1.0851 1.35 x 101 1.1303 sin 64º
8.988 x 10-11.9537 1.0840 1.002 x 10-2 2.0011 - Threc boats P, Q and R are situated in such a way that boat Q is 4.5km on a bearing of 120º from boat P. Boat R is 6km on a bearing of 030º from Q. Calculate the distance of boat R from boat P. (3mks)
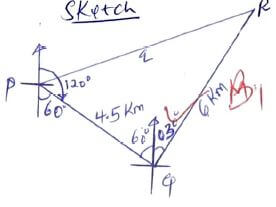
q2 = 4.52 + 62 - 2 x 4.5 x 6 cos 80º
q = √(4.5)2 + 62
= 7.5 - Simplify the expression 4x2-9x2 (3mks)
3x2-4xy-42
Numerator
= (2x - 3y) (2x + 3y)
Denominator
= 3x2 - 6xy + 2xy - 4y2
= 3x(x - 2y) + 2y (x - 2y)
= (3x + 2y)(x - 2y)
(2x - 3y)(2x + 3y)
(3x + 2y)(x-2y)
= 2x - 3y
x - 2y - In the figure ABCD shown below a parallelogram, AB=12cm and angle DAB=48

The area of the parallelogram is 36 cm', find the perimeter correct to 2 decimal places. (4mks)
1/2 ab sinθ = A
2(1/2 x 12 x AD sin 48º) = 36
12 AD sin 48º =36
AD = 36
12 sin 48º
= 4.037
perimeter = (2 x 12 + 2 x 4.037) cm
= 32.074 cm
= 32.07 cm (2 d.p.) - Find the integral values of x which satisfies the incqualities
2x 1< 7+x ≤ 3x + 1 (3mks)
2x - 1 < 7 + x .........(i)
2x - x < 7 + 1
x < 8
7 + x ≤ 3x + 1 .......(ii)
7 - 1 ≤ 3x - x
6 ≤ 2x
3 ≤ x
∴ 3 ≤ x < 8
Integral values:
3, 4, 5. 6 and 7 - Use reciprocal and cube tables to evaluate 9 - 25000 correct to 2 significant figures (3 mks)
96.96 (69.96)3
9 - 25000
9.096 x 101 (69.96)3
= 9 x 0.01 - 25000
34240
= 9 - 250
9.696 x 101 3.424 x x103
= 0.09279 - 250 x 0.0002921
= 0.09279 - 0.073025
= 0.019765
= 0.020 (2 s.f) - At the end of her stay in Kenya a French tourist had 3420 French Frances which she decided to change to Euros. Given that the exchange rate was
1 French France ksh.1 1.25
1 Euro = ksh. 72.50
Calculate the number of Buros she received if the bank charged her 2% commission to the nearest Euro. (3mks)
ksh 11.25 x 3420 = ksh 38475
Euro (38475/72.50) = Euro 530.60
commission in Euro = (2/1000 x 530.69)
= 10.6138
Euro (530.69 - 10.6138)
= Euro 520 - Three light signals have been set to flash at intervals of 15 minutes, 20 minutes and 24 minutes. If they all flash together at 1015hours, when will they next flash together? (3mks)
l.c.m = 23 x 3 x 515 20 24 2 15 10 12 2 15 5 6 2 15 5 3 3 5 5 1 5 1 1 1
= 120 minutes
= 2 hours
time =
1015h
+0200
1215 h
or
12.15 pm - Two successive translation (3 a) and (b b) respectively are the same as (8 15)
Detemine the product of a and b. (3mks)
b = 8 - 3 = 5
a = 10
a x b = 10 x 5
= 50 - Two similar solids have masses of 512g and 125g. The base area of the larger solids 192cm'. Find the area of the smaller solid. (3mks)
v.s.f = 512
125
l.s.f = 3√512/125 = 8/5
= 192/A = (8/5)2
A = 192 x 25
75
= 75 cm2 - A pick-up is loaded with a mixture of bags ofmaize and bags of beans. One bag of maize has a mass of 90kg and one bag of beans has a mass of 70kg. The pick-up is loaded with 300 bags whose total mass is 23.4 tonnes. Find the number of bags of each type it is carrying. (3mks)
90x + 70y = 23400
x + y = 300
y = (300 - x)
90x + 70(300 - x) = 23400
29x = 2400
x = 120
y = 180
maize = 120 bags
beans = 180 bags - A (2, 5), B (9, 12) and C (x, y) are vertices of a triangle.
- Find the equation of line AB in the form ax + by = c (3mks)
m = 12 - 5 = 1
9 - 2
y - 5 = 1
x - 2
y = x +3
x - y = -3
or
-x + y = 3
or
y = mx + c
5 = 1(2) + c
c = 3
y = x + 3
-x + y = 3 - Find the equation of the perpendicular bisector of line AB (3mks)
midpoint of AB
= (2 + 9, 5 + 12)
2 2
=(5.5, 8.5)
y - 8.5 = -1
x - 5.5
y = -x + 14 - Given that AC is perpendicular to AB and the equation of the line BC is y = -2x + 30
Find the coordinate of C (4mks)
Equation of AC
m = -1, A(2,5)
y - 5 = -1
x - 2
y = -x + 7
equation of BC
y = -2x + 30
y = -x + 7
y = -2x + 30
= -x + 7 = -2x + 30
x = 23
y = -16
c(-16, 23)
- Find the equation of line AB in the form ax + by = c (3mks)
- In the figure below (not drawn to scale) AB=8.5cm, AC=7.2cm, AD=7.8cm. CD=3.8 and angle CAD=48.2°

Calculate to 2 decimal places- The length BC (3mks)
(BC)2 = 8.52 + 7.22 - 2 x 7.2 x 8.5 cos 48.2º
BC2 = √42.5064
BC = 6.52 cm - The size of angle ABC (2mks)
7.2 = 6.52
sin B sin 48.2º
Sin B = 7.2 sin 48.2º
6.52
sin B = 0.8232
B = sin-1(0.8232)
= 55.41º - The size of angle CAD (3mks)
3.82 = 7.22 + 7.82 - 2 x 7.2 x 7.8 cos A
112.32 cos A = 98.24
cos A = 0.8746
A = cos-1 (0.8746)
= 29.00º or 28.26º - The radius of a circle that passes through the vertices of triangle ABD (2mks)
BD = (3.8 + 6.52) = 10.32
< BAD = (48.2 + 29) = 77.2º
2R = 10.32
sin 77.2
R = ( 10.32 )
2 sin 77.2º
= 5.29 cm
7.8 = 2R
sin 55.41
= 4.74cm
- The length BC (3mks)
- The height of 50 seedlings in a nursery were measured to the nearest centimeters and recorded as shown below
25 23 33 29 34 25 23 31 37 31
31 28 16 23 21 36 32 36 42 40
35 22 21 27 30 19 34 27 38 22
32 31 28 29 24 20 29 35 17 15
28 40 32 27 26 23 20 32 26 28- Make a grouped frequency table with a class width of5 starting with 15 (3mks)
class x tally f fx cf 15-19 17 IIII 4 68 4 20-24 22 IIII IIII I 11 242 15 25-29 27 IIII IIII IIII 14 378 29 30-34 32 IIII IIII II 12 384 41 35-39 37 IIII I 6 222 47 40-44 42 III 3 126 50 - Calculate to 2 decimal places
- The mean height (4 mks)
X = 1420
50
= 28.40 (2 d.p) - The media height (3mks)
= 24.5 + 25 - 15 x 5
29
= 26.22 (2 d.p)
- The mean height (4 mks)
- Make a grouped frequency table with a class width of5 starting with 15 (3mks)
- Two towns P and Q are 580km apart. A bus left town P at 6.10am and maintains an average speed of 90km/h between P and Q. A car left Q at 8:00am and travelled towards P at an average specd of 120km/h.
-
- How far from town P did they meet? (4mks)
P I---------------------------------------------I Q
6.10 cm 8.00 cm
0800h - 0600h = 15/6h
d = (90 x 15/6) = 165 km
Dr = 580 - 165 - 415km
SR = (90 + 120) km/h
= 210 km/h
T = 415 h
210
= 83/42
T - 15/6 + 83/42 = 80/21 h or 580 - 120 x 415
40
D = 80/21 x 90 km
= 3426/7 km or 342.86km - At what time did they meet (4mks)
8.00 cm
1.59 cm
9.59 cm
- How far from town P did they meet? (4mks)
- A rally driver starts from Q towards town P at 10:00am. If its average speed was 180km/h. Calculate
- The time taken for the rally driver overtook the car (4mks)
DR = 2 x 120 km
= 240
SR = (180 - 120) km
= 60 km
T = 240/60 h
= 4 hours - The time when the rally driver overtook the car (1mk)
Time:
1000 h
+0400 h
1400 h
= 2:00 pm
- The time taken for the rally driver overtook the car (4mks)
-
- A triangle ABCD with vertices A(1,1), B(3,-1) and C(4,2) is mapped unto triangle A'B'C' with vertices A'(-l,-1), B'(1,-3) and C' (-2,-4).
- On the grid provided draw triangle ABC and A' B'C (Zmks)
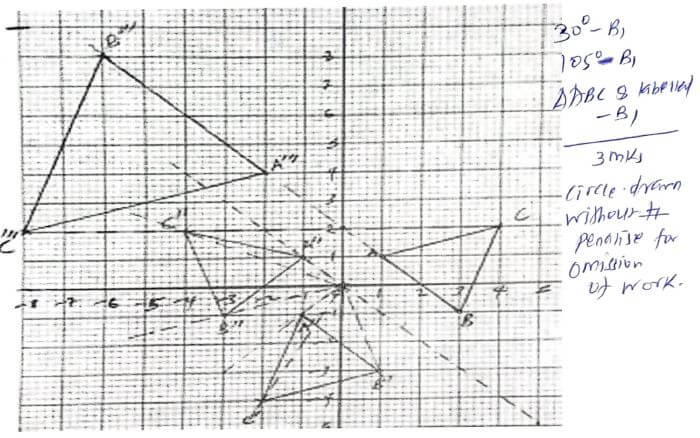
- Describe the transformation that maps ABC unto A'B'C (2mks)
Reflection in the line y = -x - A'BC" is the image of A'B'c' under negative quarter turn about the origin. Draw the triangle A "B"C'" and state the coordinates. (2mks)
AII(-1,1), BII(-3,-1), CII(-4,2) - ABC is mapped unto A'"B"'C''' by an enlargement center (0, 2) and scale factor -2.
Draw AIIIBIIICIII (2mks)
AIII(-2,4), BIII(-6,8), CIII(-8,2) - Given that the area of triangle ABC is 7.5cm2. Calculate the area of triangle A'''B'''C''' (2mks)
7.5 = (1/2)2
A
A = 30 cm2
- On the grid provided draw triangle ABC and A' B'C (Zmks)
-
- Given that the matrix
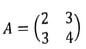 . Find A . (2mks)
. Find A . (2mks)
Det = 4 x 2 - 33 = -1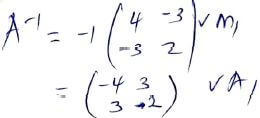
- Moi Siongiroi Girls' bought 200bags of sugar and 300 bags of rice for a total cost of ksh.850000. Tenwek boys' bought 90 bags of sugar and 120 bags of rice at a total of ksh.360000 from the same store as Moi Siongiroi Girls'. If the price of a bag of sugar is ksh. X and that of rice is ksh. Y.
- Fom a matrix equation to represent the above information (2mks)
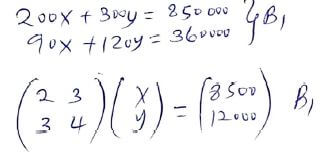
- Use the matrix A" to fine the price of one bag of each item (3mks)
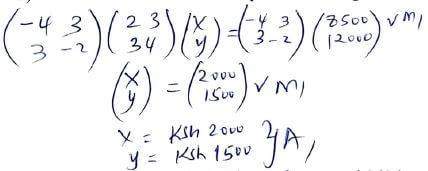
- Kipsigis Girls' bought 225 bags of sugar and 360 bags of rice from the same store. The school was given a total discount of ksth. 33,300. If the discount on the rice of a bag of rice was 2%. Calculate the percentage discount on the price of a bag of sugar. (3mks)
profile per bag of rice
ksh(0.98 x 1500)
= ksh 1470
discount = ksh (1500 - 1470)
= ksh 30
total discount = ksh 30 x 360
= ksh 10800
discount for sugar
= ksh 33300 - 10800
= ksh 22500
d(225) = 22500
d = ksh 100
% discount = 100 x 10%
2000
= 5%
- Fom a matrix equation to represent the above information (2mks)
- Given that the matrix
- The figure below represents a conical flask. The flask consists of hemispherical top lid cylindrical neck, frustum part and hemispherical base. The vertical height of the flask is 21 cm. The diameter of the cylindrical part is 4cm while that of the conical base is 10 cm.

Calculate, correct to 1 decimal places- The slanting height of the frustum part (2mks)
h = √102 + 32
= 10.4 cm - The slant height of smaller cone that was cut off to make the frustum part (2mks)
x = 2/5
x + 10.4
5x = 2x + 20.8
3x = 20.8
x = 6.9 cm - The external surface area of the flask (take T=3.142) (4mks)
A1 = 2 x 3.142 x 2 x 4
= 50.272 cm2
A2 = 3.142 x 5 x 17.7 - 3.142 x 2 x 69
= 234.71 cm2
A3= 2 x 3.142 (52 + 22)
= 182.236 cm2
At = 50.272 + 234.71 + 182.236
= 467.2 cm2 - The mass of the liquid in the hemispherical base is 204g. find the density of the liquid. (2mks)
p = 204
1/2 x 4/3 x 3.142 x 53
=0.7791
= 0.8 g/cm3
- The slanting height of the frustum part (2mks)
- Using a ruler and a pair of compasses only, construct,
-
- Triangle ABC in which AB-Scm, <BAC=30º and <ABC=105º (3mks)
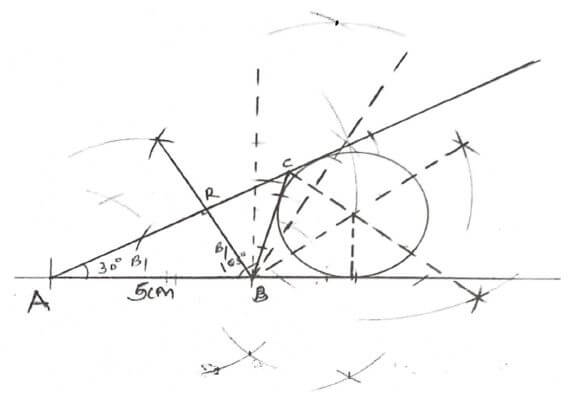
- A circle that touches line AC produced, AB produced and line BC. Measure the radius. (3mks)
R = 2 ± 0.1 cm
Bisector of two angle - B1
Circle drawn - B1
- Triangle ABC in which AB-Scm, <BAC=30º and <ABC=105º (3mks)
- Drop a perpendicular line from pointB to meet AC at R. measure BR (2mks)
BR = 2.5 ± 0.1 cm -A1
Dropping ± - B1 - Determine the area of triangle ABC (2mks)
A = (1/2 x 6.7 x 2.5)
= 8.375 cm
A = 1/2 x 6.6 x 2.4
= 7.92 cm2
A = 1/2 x 6.8 x 2.6 cm2
= 8.84cm2
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Eagle II Joint 2021 Mock Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

