INSTRUCTIONS TO CANDIDATES
- Answer ALL the questions in Section I and ONLY five questions from section II in the spaces provided below each question
- Show all the steps in your calculations, giving your answers at each stage. Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
For Examiner’s Use only
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |

QUESTIONS
SECTION I (50 MARKS)
Answer ALL questions in this section.
- Make y the subject of the formula in:
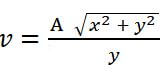 (3 marks)
(3 marks) - Solve for x in the equation: Log8 (6-2x) - Log8 (x - 2) = -1⁄3 (3 marks)
- Three quantities P, Q and R are such that P varies directly as the cube of Q and inversely as the square root of R. Find the percentage change in P if Q decreases by 10% and R decreases to 36%. (3 marks)
- A circle with its centre at O (-2, 0) passes through a point (1, 4). Write down the equation of the circle in the form x2+y2+ax+by+c=0 (3 marks)
- Express:
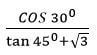 in surd form and simplify by rationalizing the denominator (3 marks)
in surd form and simplify by rationalizing the denominator (3 marks) - The position vectors of points P and Q are p = -2i - j + k and q =4i -5j – 2k and respectively. Find the magnitude of OM if M is a point that divides PQ in the ratio 1:2 correct to 4 significant figures. (3 marks)
-
- Find the binomial expansion of
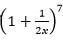 up to the 4th term with increasing powers of x. (2 marks)
up to the 4th term with increasing powers of x. (2 marks) - Hence estimate the value of (1.05)7 correct to 4 decimal places. (2 marks)
- Find the binomial expansion of
- A computer with a marked price of Kshs. 40000 can also be bought on hire purchase terms. Kibet bought the computer on hire purchase by making a deposit of Ksh 10000 and cleared the balance with equal 12 monthly installments of KShs. 3500 each. Determine the monthly interest rate of hire purchase to 2 significant figures. (3 marks)
- A dealer blends Kericho tea that costs sh 300 per 100g packet with Ketepa that costs ksh 160 per 200g packet. In what ratio must the dealer mix the two so that by selling a 100g packet of the blend for ksh 250, a profit of 25% is made? (4 marks)
- Solve for x in the equation: Sin 2θ=-0.5 for 00 ≤ θ≤ 3600 (3 marks)
- Use completing of the square method to solve: 2x2-6x+4=0 (3 marks)
- A carpenter wishes to cut a 1m long piece of wood into 3 equal parts. He approximates the length of each piece to 0.33m. Calculate the percentage error due to this approximation (3 marks)
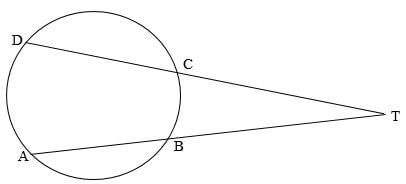
- Calculate length DT in the figure below given AT and DT are secants that intersect at T and AB = 5 cm, BT = 4 cm and DC = 9 cm. (3 marks)
- An arc of a circle of diameter 7 cm subtends an angle of 1.2 radians to the centre of the circle. What is the length of the arc? (2 marks)
- Given matrix
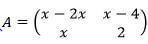 . Find the possible values of x if A is a singular matrix. (3 marks)
. Find the possible values of x if A is a singular matrix. (3 marks) - Working together two taps A and B can fill a tank in 2 hours. By itself tap A can fill the tank in 6 hrs. Tap A and B are opened at the same time and after running for 1 hours, an outlet tap which can drain the full tank by itself in 12 hours is opened and Tap A is closed. Find the total time taken to fill the tank. (4 marks)
SECTION II – 50 MARKS
Answer only FIVE questions from this section. - In a form 4 class there are 24 girls and 30 boys. The probability that a girl participates in games is 0.4 whereas that of a boy is 0.6.
- A student is picked at random from the class. Find the probability that the student picked:
- Is a boy and will participate in games (2 marks)
- Will not participate in games (2 marks)
- Two similar bags A and B are such that, bag A contains 3 blue balls and 7 red balls while bag B contains 4 green balls and 8 blue balls. The balls are similar in shape and size. A ball is drawn from bag A and bag B. Determine the probability that:
- One of the balls drawn is green. (2 marks)
- The balls drawn are of the same colour. (2 marks)
- None of the balls drawn is red (2 marks)
- A student is picked at random from the class. Find the probability that the student picked:
- The table below gives the values of P and I showing the relationship between electrical power (P) and current (I) in a certain circuit.
P
1.050
1.350
1.650
1.950
2.250
2.400
I
0.995
1.697
2.700
3.698
4.403
5.196
- Using a scale of 1 cm to represent 0.5 units on the horizontal axis and 2 cm to represent 0.5 units on the vertical axis, draw a graph of P against I on the grid provided.(4 marks)

- What is the gradient of the graph? (2 marks)
- From the graph, find:
- The value of P when I = 3.4 (1 mark)
- The value of I when P = 1.45 (1 mark)
- The value of P when I = 0 (2 marks)
- Using a scale of 1 cm to represent 0.5 units on the horizontal axis and 2 cm to represent 0.5 units on the vertical axis, draw a graph of P against I on the grid provided.(4 marks)
- In the triangle OAB below, OA = a, OB = b and 3OA = 2OC. M divided OB in the ratio 1:1 .
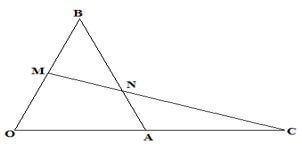
- Express in terms of a and b only, the vectors
- BA (1 mark)
- OC (1 mark)
- MC (1 mark)
- Given further that MN = hMC and BN = kBA,
- Express vector MN in two different ways in terms of a, b, h and k (2 marks)
- Find the value of h and k. (4 marks)
- State the ratio MN:MC (1 mark)
- Express in terms of a and b only, the vectors
- A group of people planned to contribute equally towards buying a plot valued at Ksh 270,000. After the contribution, 2 members joined of the group. As a result, a refund of Ksh 1500 was made to the members who had already contributed.
- Let the original number of people be x and express in terms of x:
- The original contribution (1 mark)
- The new contribution (1 mark)
- Find how much each member contributed finally (5 marks)
- Calculate the percentage decrease in the contribution per person caused by the members who joined. (3 marks)
- Let the original number of people be x and express in terms of x:
- The table shows income tax rates for a certain year.
A company employee earns a monthly basic salary and is also given taxable allowances amounting to Ksh 10480. If the employees tax on the 5th band is Ksh 3420,Monthly taxable pay K£
Rate of tax in Ksh. Per K£
1- 434
435 - 866
867- 1298
1299 - 1730
Over 1730
2
3
4
5
6
- Calculate the employee’s monthly taxable income tax in K£. (2 marks)
- The employee is entitled to a personal tax relief of Ksh. 1056 per month. Determine the net tax. (4 marks)
- In a certain month, the employee received a 25% increment in his basic salary. Calculate his net monthly pay. (4 marks)
-
- The nth term of a sequence is given by the relation 2n+n
- Write down the first 3 terms of the sequence. (1 mark)
- Find the sum of the first 42 terms of the sequence. (3 marks)
- Bacteria in a culture increases by 125% of every hour. The number bacteria in the culture at 0607h was 8000.
- What will be the number of the bacteria in the culture after one hour.(2 marks)
- Determine the total number of bacteria in the culture at 0937h the same day (4 marks)
- The nth term of a sequence is given by the relation 2n+n
- In the figure above, ABC is a tangent to the circle, centre O and BOE is a diameter. Given FG = BG and angles DBC = 48º angle GEF = 25º.
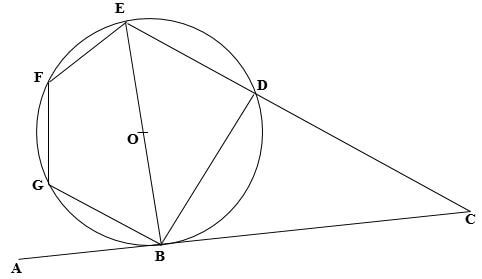
Giving reasons, find the size of angles:- BFE (2 marks)
- BGD (2 marks)
- DFE (2 marks)
- Reflex DOE (2 marks)
- BGF (2 marks)
-
- Complete the table below for y = -2 sin x and y = 3 cos x. (2 marks)
x
0°
30°
60°
90°
120°
150°
180°
210°
240°
270°
300°
330°
360°
-2 Sin x
0.00
-1.73
-1.00
0.00
2.00
1.73
3 Cos x
3.00
1.50
-2.60
-3.00
0.00
1.50
- Draw the graph y = -2 Sin x and y = 3 cos x using 1 cm to represent 30° horizontal axis and 2 cm to represent 1 unit on the vertical axis. (5 marks)

- Use the graph to solve:
- 3 Cos x + 2sin x = 0 (1 mark)
- 1 - 2sin x = 2 (2 marks)
- Complete the table below for y = -2 sin x and y = 3 cos x. (2 marks)

MARKING SCHEME
SECTION I (50 MARKS)
Answer ALL questions in this section.
- Make y the subject of the formula in:
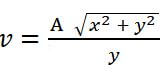 (3 marks)
(3 marks)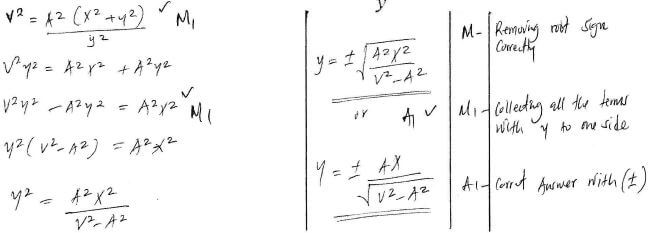
- Solve for x in the equation: Log8 (6-2x) - Log8 (x - 2) = -1⁄3 (3 marks)

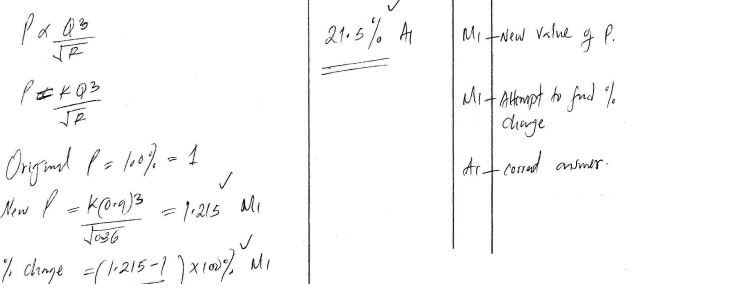
- Three quantities P, Q and R are such that P varies directly as the cube of Q and inversely as the square root of R. Find the percentage change in P if Q decreases by 10% and R decreases to 36%. (3 marks)
- A circle with its centre at O (-2, 0) passes through a point (1, 4). Write down the equation of the circle in the form x2+y2+ax+by+c=0 (3 marks)
r2 = (4 - 0)2 + (1 - -2)2
= 25
(x + 2)2 + (y - 0)2 = 25
x2 + 4x + y2 + 4 = 25
x2 + y2 + 4x - 21 = 0
or
x2 + y2 + 4x = 21 - Express:
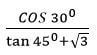 in surd form and simplify by rationalizing the denominator (3 marks)
in surd form and simplify by rationalizing the denominator (3 marks)
- The position vectors of points P and Q are p = -2i - j + k and q =4i -5j – 2k and respectively. Find the magnitude of OM if M is a point that divides PQ in the ratio 1:2 correct to 4 significant figures. (3 marks)
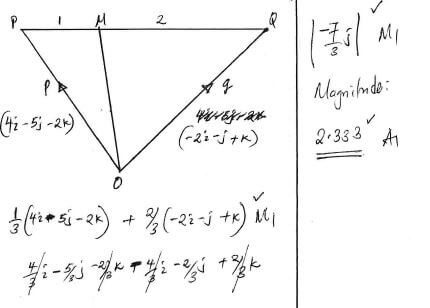
-
- Find the binomial expansion of
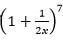 up to the 4th term with increasing powers of x. (2 marks)
up to the 4th term with increasing powers of x. (2 marks)
17 + 7.(1/2x)2 + 21.(1/2x)2 +3.5(1/2x)3
1 + 7/2x + 21/4x2 + 35/8x3 - Hence estimate the value of (1.05)7 correct to 4 decimal places. (2 marks)
0.05 = 1/2x
2x = 1/0.05
x = 10
1 + 7/2(10) + 21(4(100) + 35/8(1000)
1 + 0.35 + 0.0525 + 0.004325
= 1.406875
= 1.4069
- Find the binomial expansion of
- A computer with a marked price of Kshs. 40000 can also be bought on hire purchase terms. Kibet bought the computer on hire purchase by making a deposit of Ksh 10000 and cleared the balance with equal 12 monthly installments of KShs. 3500 each. Determine the monthly interest rate of hire purchase to 2 significant figures. (3 marks)
new principal = 40000 - 10000 = 30000
amount = 12 x 3500 = 42000
42000 = 30000(1 + r/100)12
1.4(1 + r/100)12
1.02846 = 1 + r/100
= 0.02846 x 100
= 2.846
= 28% - A dealer blends Kericho tea that costs sh 300 per 100g packet with Ketepa that costs ksh 160 per 200g packet. In what ratio must the dealer mix the two so that by selling a 100g packet of the blend for ksh 250, a profit of 25% is made? (4 marks)
let kericho be x - 100/300
ketepa be y - 100/80
250 --> 125%
? --> 100%
100 x 250 = 200
125
300x + 80y = 200
x + y
300x + 80y = 200x + 200y
x/y = 120/100
x:y = 6:5 - Solve for x in the equation: Sin 2θ=-0.5 for 00 ≤ θ≤ 3600 (3 marks)
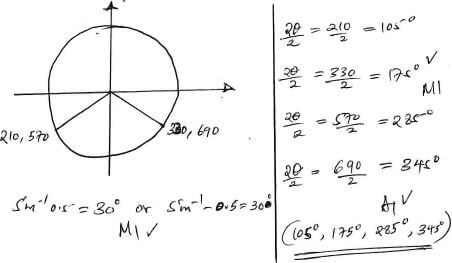
- Use completing of the square method to solve: 2x2-6x+4=0 (3 marks)
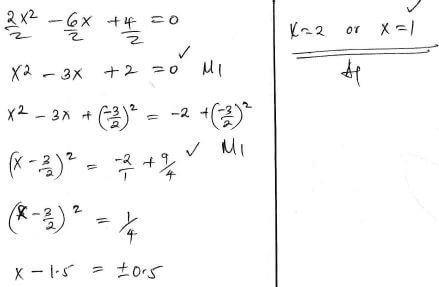
- A carpenter wishes to cut a 1m long piece of wood into 3 equal parts. He approximates the length of each piece to 0.33m. Calculate the percentage error due to this approximation (3 marks)
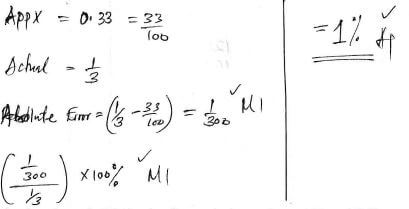
- Calculate length DT in the figure below given AT and DT are secants that intersect at T and AB = 5 cm, BT = 4 cm and DC = 9 cm. (3 marks)

x(x + 9) = 9 x 4
x2 + 9x = 36
x2 + 9x - 36 = 0
x2 - 3x + 12x - 36 = 0
x(x - 3) + 12 (x - 3) = 0
(x + 12)(x - 3) =
x = -12 or x = 3
DT = 3 + 9
= 12 cm - An arc of a circle of diameter 7 cm subtends an angle of 1.2 radians to the centre of the circle. What is the length of the arc? (2 marks)
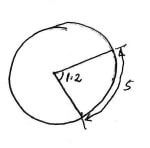
θ = 5/r
s = θr
s = 1.2 x 3.5
Arc length = 4.2cm - Given matrix
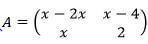 . Find the possible values of x if A is a singular matrix. (3 marks)
. Find the possible values of x if A is a singular matrix. (3 marks)
2(x - 2x) = x(x - 4)
2x - 4x = x2 - 4x
x2 - 2x = 0
x(x - 2) = 0
x = 0 or x = 2 - Working together two taps A and B can fill a tank in 2 hours. By itself tap A can fill the tank in 6 hrs. Tap A and B are opened at the same time and after running for 1 hours, an outlet tap which can drain the full tank by itself in 12 hours is opened and Tap A is closed. Find the total time taken to fill the tank. (4 marks)
let the whole tank be x
After - 1hr, filled = 1/2x
- Reminder = 1/2x
Rate tap B
1/2 - 1/6 = 1/3
Tap B and Tap C
1/3 - 1/12 = 1/4
1/4 - 1 hr
1/2x - ?
1/2 x 1 = 2 hrs
1/4
total time:
2 hrf 1 hr
= 3 hrs
SECTION II – 50 MARKS
Answer only FIVE questions from this section. - In a form 4 class there are 24 girls and 30 boys. The probability that a girl participates in games is 0.4 whereas that of a boy is 0.6.
- A student is picked at random from the class. Find the probability that the student picked:
- Is a boy and will participate in games (2 marks)
30/54 x 0.6 = 1/3 - Will not participate in games (2 marks)
BG' or GG'
(30/54 x 0.4) + (24/54 x 0.6) = 22/45
- Is a boy and will participate in games (2 marks)
- Two similar bags A and B are such that, bag A contains 3 blue balls and 7 red balls while bag B contains 4 green balls and 8 blue balls. The balls are similar in shape and size. A ball is drawn from bag A and bag B. Determine the probability that:
- One of the balls drawn is green. (2 marks)
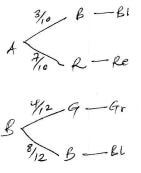
p(green) = 4/12 or 1/3 - The balls drawn are of the same colour. (2 marks)
P(B1) and P(B1)
3/10 x 8/12 = 24/120
= 24/100 or 1/5 - None of the balls drawn is red (2 marks)
1 - P(Red)
= (1 - 7/10) = 3/10
- One of the balls drawn is green. (2 marks)
- A student is picked at random from the class. Find the probability that the student picked:
- The table below gives the values of P and I showing the relationship between electrical power (P) and current (I) in a certain circuit.
P
1.050
1.350
1.650
1.950
2.250
2.400
I
0.995
1.697
2.700
3.698
4.403
5.196
- Using a scale of 1 cm to represent 0.5 units on the horizontal axis and 2 cm to represent 0.5 units on the vertical axis, draw a graph of P against I on the grid provided.(4 marks)
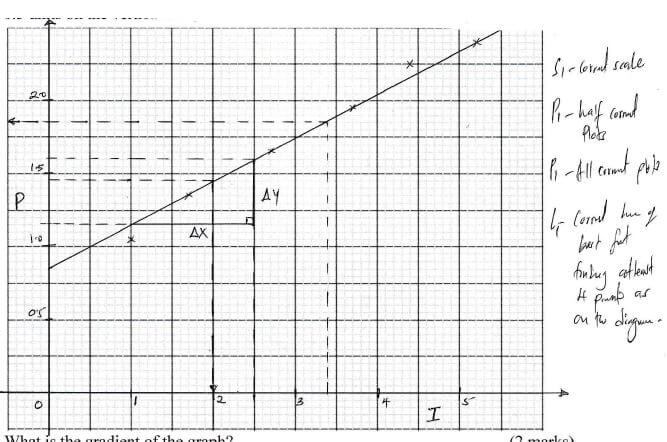
- What is the gradient of the graph? (2 marks)
Gradient = Δy
Δx
= (1.6 - 1.15) = 0.45
(2.5 - 1) 1.5
= 0.3 ± 0.1 - From the graph, find:
- The value of P when I = 3.4 (1 mark)
p = 1.85 ± 0.05 - The value of I when P = 1.45 (1 mark)
I = 2 ± 0.5 - The value of P when I = 0 (2 marks)
p = 0.65 ± 0.5
- The value of P when I = 3.4 (1 mark)
- Using a scale of 1 cm to represent 0.5 units on the horizontal axis and 2 cm to represent 0.5 units on the vertical axis, draw a graph of P against I on the grid provided.(4 marks)
- In the triangle OAB below, OA = a, OB = b and 3OA = 2OC. M divided OB in the ratio 1:1 .

- Express in terms of a and b only, the vectors
- BA (1 mark)
-b + a or a + b - OC (1 mark)
OC = 3/2OA = 3/2a - MC (1 mark)
-1/2b + 3/2a or 3/2 - 1/2b
- BA (1 mark)
- Given further that MN = hMC and BN = kBA,
- Express vector MN in two different ways in terms of a, b, h and k (2 marks)
h(3/2a - 1/2b) = 3/2ha - 1/2hb ........(i)
1/2b - kb + ka ..................(ii) - Find the value of h and k. (4 marks)
3/2ha - 1/2hb = 1/2b - kb + ka
3/2h = k .....................(i)
-1/2 = (1/2 - k) ...........(ii)
-1/2h = 1/2 - 3/2h
h = 1/2
k = 3/4
- Express vector MN in two different ways in terms of a, b, h and k (2 marks)
- State the ratio MN:MC (1 mark)
MN:MC
2:1
- Express in terms of a and b only, the vectors
- A group of people planned to contribute equally towards buying a plot valued at Ksh 270,000. After the contribution, 2 members joined of the group. As a result, a refund of Ksh 1500 was made to the members who had already contributed.
- Let the original number of people be x and express in terms of x:
- The original contribution (1 mark)
270000
x - The new contribution (1 mark)
270000
x + 2
- The original contribution (1 mark)
- Find how much each member contributed finally (5 marks)
270000 - 270000 = 1500
x x + 2
1/x - 1/x + 2 = 1/180
180(x + 2) - 180x = x2 + 2x
180x + 360 - 180x = x2 + 2x
x2 + 2x - 360 = 0
x = -2 ± √ 4 + 1440
2
x = 18 or x = - 20
New no: 18 + 2 = 20
270000
20
ans = 13500 - Calculate the percentage decrease in the contribution per person caused by the members who joined. (3 marks)
initial contribution = 270000
18
= 15000
1500 x 100%
15000
= 10%
- Let the original number of people be x and express in terms of x:
- The table shows income tax rates for a certain year.
A company employee earns a monthly basic salary and is also given taxable allowances amounting to Ksh 10480. If the employees tax on the 5th band is Ksh 3420,Monthly taxable pay K£
Rate of tax in Ksh. Per K£
1- 434
435 - 866
867- 1298
1299 - 1730
Over 1730
2
3
4
5
6
- Calculate the employee’s monthly taxable income tax in K£. (2 marks)
3420 = 570
6
570 + 1730 = 2300 - The employee is entitled to a personal tax relief of Ksh. 1056 per month. Determine the net tax. (4 marks)
434 x 2 = 868
432 x 3 = 1296
432 x 4 = 1728
432 x 5 = 2160
+ 3420
9472
9472 - 1056 = 8416 - In a certain month, the employee received a 25% increment in his basic salary. Calculate his net monthly pay. (4 marks)
Basic salary - (2300 - 10480/20) = 1776
25% basic salary - 1776 x 0.25 = 444
change in tax - 444 x 6 = 2664
Total tax - 2664 + 8416 = 11080
Total gross income: (2300 + 444) x 20
= 54 880
54 880 - 11080
= 43 800
- Calculate the employee’s monthly taxable income tax in K£. (2 marks)
-
- The nth term of a sequence is given by the relation 2n+n
- Write down the first 3 terms of the sequence. (1 mark)
3, 5, 7 - Find the sum of the first 42 terms of the sequence. (3 marks)
d = 5 - 3 = 2
Sn = 42/2(2(3) + (2 2 - 1)2)
= 1785
- Write down the first 3 terms of the sequence. (1 mark)
- Bacteria in a culture increases by 125% of every hour. The number bacteria in the culture at 0607h was 8000.
- What will be the number of the bacteria in the culture after one hour.(2 marks)
8000 x 2.25 = 18000 - Determine the total number of bacteria in the culture at 0937h the same day (4 marks)
r = 18000/8000 = 2.25
R = 0937 - 0607 = 31/2
8000 (2.25)n - 1
8000 (2.25)5/2
= 60750
- What will be the number of the bacteria in the culture after one hour.(2 marks)
- The nth term of a sequence is given by the relation 2n+n
- In the figure above, ABC is a tangent to the circle, centre O and BOE is a diameter. Given FG = BG and angles DBC = 48º angle GEF = 25º.

Giving reasons, find the size of angles:- BFE (2 marks)
90º - angles subtended by diameter to circumference
= 90º - BGD (2 marks)
48º - angles on alternate segments are equal - DFE (2 marks)
42º - angles substended by the same chords / arc - Reflex DOE (2 marks)
276º - angle subtended by a chord to the centre is twice to the circumference - BGF (2 marks)
130º - opposite angles of a cyclic quadrilateral add to 180º
- BFE (2 marks)
-
- Complete the table below for y = -2 sin x and y = 3 cos x. (2 marks)
x
0°
30°
60°
90°
120°
150°
180°
210°
240°
270°
300°
330°
360°
-2 Sin x
0.00
-1.00 -1.73
-2.00 -1.73 -1.00
0.00
1.00 1.73 2.00
1.73
1.00 0.00 3 Cos x
3.00
2.60 1.50
0.00 -1.50 -2.60
-3.00
-2.60 -1.50 0.00
1.50
2.60 3.00 - Draw the graph y = -2 Sin x and y = 3 cos x using 1 cm to represent 30° horizontal axis and 2 cm to represent 1 unit on the vertical axis. (5 marks)

- Use the graph to solve:
- 3 Cos x + 2sin x = 0 (1 mark)
120º ≤ x ≤ 125º - 1 - 2sin x = 2 (2 marks)
-25 h x = 1
210º and 330º
- 3 Cos x + 2sin x = 0 (1 mark)
- Complete the table below for y = -2 sin x and y = 3 cos x. (2 marks)
Download Mathematics Paper 2 Questions and Answers - Eagle II Joint 2021 Mock Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

