QUESTIONS
SECTION I (50 Marks)
Answer all the questions in this section.
- Use logarithms only to evaluate, correct to 4 decimal places. (4 marks)
∛0.4591 × 7.8052
629.3 - Without using a calculator or mathematical tables, evaluate, leaving your answer in the form a√b+c , where a, b and c are integral values (3 marks)
tan6º
1 - cos30º - Calculate the percentage error in the volume of a cone of radius 7.0 cm and height 20 cm. (3 marks)
- Make Q the subject of the formula (3 marks)
x= 3a+2bQ2
Q2 - 2 - Three quantities P, Q and R are such that P partly varies as Q and partly varies inversely as R. The table below shows the values of P, Q and R.
Using c and k as constants of proportionality, find the law connecting P, Q and R. (4 marks)P Q R 8 1 0.5 14 2 0.3 - The figure below, O is the centre of the circle. P joined to Q passes through O

- Calculate the radius and centre of the circle. (2 marks)
- Express the equation of the circle in the form (x-a)2+(y-b)2=r2 (2 marks)
- 3 kilograms of Korie rice costing Kshs. 120 per kilogram is mixed with a kilogram of Basmati rice that costs Kshs. 200 per kilogram. At what cost should the mixture be sold to realize a profit of 25%? (3 marks)
- In the figure below, chords AB and CD intersect externally at Q. If AB=5cm, BQ = 6cm and DQ=4cm.
 Calculate the length of CD. (3 marks)
Calculate the length of CD. (3 marks) - The probability that a student wakes up in time is 4/5. If he does so, the probability that he finds the school bus is 11/12. Otherwise, the probability that he misses the school bus is 2/3
- Draw a tree diagram to represent the information above. (1 mark)
- Calculate the probability that the student finds the school bus. (2 marks)
- Apudo wants to buy a computer on hire purchase. The cash price of the computer is Kshs. 40, 000. Apudo makes a down payment of Kshs. 14, 000 followed by 16 equal monthly instalments of Kshs. 2,625. Calculate the rate of compound interest per month correct to 2 decimal places. (3 marks)
- Without using mathematical tables or a calculator, find the value of x in log2(2x-3)+1 = log21+log2(3x+2) (3 marks)
- Solve for x in the equation: (3 marks)
sin(3x+30º )=√3/2 for 0º≤x≤180º - The figure below shows a right pyramid VABCD of a rectangular base. AB=6 cm, BC=12 cm and VA=VB=VC=VD=16cm.
 Calculate the angle VD makes with the base ABCD. (3 marks)
Calculate the angle VD makes with the base ABCD. (3 marks) - Use the quadratic formula to solve for x in 2x2+7x-15=0. (3 marks)
- Two similar cylindrical containers have surface areas of 448 cm2 and 2800 cm2. Given that the capacity of the larger container is 2.5 litres, calculate the volume of the smaller container in cubic centimetres. (3 marks)
-
- Expand and simplify (1+x/2)6 in ascending powers of x up to the term in x3 (1 mark)
- Use your expansion to estimate the value of (0.99)6 (2 marks)
SECTION II (50 Marks)
Answer any five questions in this section.
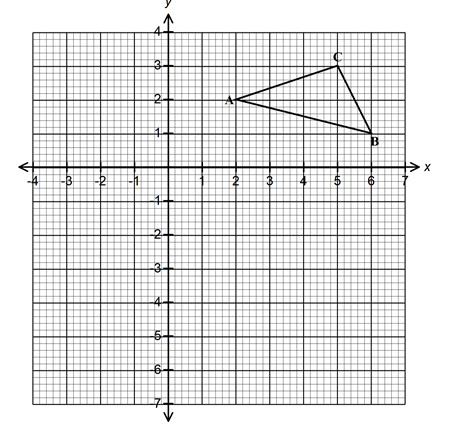
- The figure below shows a triangle ABC.
- A transformation represented by a matrix
 maps triangle ABC onto triangle A'B'C'.
maps triangle ABC onto triangle A'B'C'.- On the same grid, plot and draw triangle A'B'C'. (3 marks)
- State the coordinates of triangle A'B'C'. (1 mark)
- Another transformation represented by a matrix N maps triangle A'B'C' onto triangle A''B''C'' such that A''(-2,-2), B''(-1,-6) and C''(-3,-5)
- Draw triangle A''B''C'' (1 mark)
- Find the matrix N (3 marks)
- Describe a single transformation that maps triangle ABC on to triangle A''B''C'' (2 marks)
- A transformation represented by a matrix
- The marks scored by 40 students in a Mathematics Olympiad were shown in the table below
Marks (%) 37 – 41 42 – 46 47 – 51 52 – 56 57 – 61 62 – 66 Number of Students 3 4 10 12 8 3 -
- Using an assumed mean 49, calculate the mean marks (4 marks)
- Calculate the standard deviation (3 marks)
- Calculate the quartile deviation (3 marks)
-
- A car park in Bondo town has an area of 4,000 m2 with spaces for cars and vans. Each car requires 40 m2 of space and each van requires 50 m2. There must be a space for at least 60 vehicles. The parking spaces for cars must be more than 30 and at least 10 for vans.
- By letting x to represent the number of cars and y to represent the number of vans, write down all the inequalities that represent the above information. (4 marks)
- On the graph provided, represent the inequalities in (a) above and shade the unwanted region. (4 marks)

-
- The company charges Kshs. 300 for parking each car and Kshs. 500 for parking each van. Find the number of cars and the number of vans that would give the maximum income. (1 mark)
- Hence, find the maximum income. (1 mark)
- A particle moving with acceleration a=(10-t) m/s2. When t=1, velocity v=2 m/s and when t=0, displacement S=0 metres.
- Express S and v in terms of t. (4 marks)
- Calculate the velocity when t=3 seconds (2 marks)
- Find the displacement when t=5 seconds. (2 marks)
- Calculate the maximum velocity attained by the particle. (2 marks)
- Triangle OAB is such that OA=a and OB=b. Point C divides OA in the ratio 1: 3 and point D divides AB in the ratio 5: 2. CB and OD intersect at E
- Express the following vectors in terms of a and b
- OD (2 marks)
- BC (1 mark)
- Given that OE=kOD and CE=hCB, express OD in terms of:
- k,a and b (1 mark)
- h, a and b (2 marks)
- Find the values of h and k (3 marks)
- Give the ratio in which O divides ED (1 mark)
- Express the following vectors in terms of a and b
-
- The first and the last terms of an arithmetic progression are 4 and 134 respectively. Given that the sum of the terms is 1,863,
- The number of terms in the sequence (2 marks)
- The common difference of the sequence (2 marks)
- The third, fifth and eighth terms of another Arithmetic Progression form the first three consecutive terms of a Geometric Progression. If the common difference of the Arithmetic Progression is 3, find:
- Ther first term of the Geometric Progression. (4 marks)
- The sum of the first twelve terms of the Geometric Progression. (2 marks)
- The first and the last terms of an arithmetic progression are 4 and 134 respectively. Given that the sum of the terms is 1,863,
-
- Complete the table below to two decimal places for the functions y=sin(θ+3º) and y=2 cos(θ+30º ) for 0º≤θ≤270º (2 marks)
θº 0 30 60 90 120 150 180 210 240 270 sin(θ+30º) 0.50 0.00 -0.50 -0.87 2 cos(θ+30º) 1.73 0.00 -1.73 1.00 - On the same axes, draw the graphs of y=sin(θ+3º ) and y=2 cos(θ+30º) for 0º≤θ≤270º
Use the scales: 1 cm for 300 in the x-axis and 2 cm represents 1 unit in the y-axis. (5 marks)
- State the amplitude and period of each function. (2 marks)
- Use the graph to find the values of θ such that 2 cos(θ+30º )-sin(θ+30º)=0 (1 mark)
- Complete the table below to two decimal places for the functions y=sin(θ+3º) and y=2 cos(θ+30º ) for 0º≤θ≤270º (2 marks)
- In an experiment involving two variables W and t, the following results were obtained.
W 1.0 1.5 2.0 2.5 3.0 3.5 t 1.50 1.45 1.30 1.25 1.05 1.00 - On the grid provided, draw the line of best fit for the data. (4 marks)

- The variables t and W are connected by the equation t=cW+k, where c and k are constants
Determine:- The values of c and k; (3 marks)
- The equation of the line drawn in (a) above; (1 mark)
- Use your graph to find:
- Value of W when t=0 (1 mark)
- Value of t when W=2.8 (1 mark)
- On the grid provided, draw the line of best fit for the data. (4 marks)
Download Mathematics Paper 2 Questions - Bondo Mocks 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students